La rappresentazione dei dati in fisica

Uno degli strumenti che la fisica utilizza per rappresentare i dati è il piano cartesiano. Con le sue due assi perpendicolari – l’asse orizzontale (x) e l’asse verticale (y) – il piano cartesiano consente di visualizzare e analizzare dati in maniera bidimensionale. Ogni punto sul grafico rappresenta una specifica combinazione di valori x e y, fornendo una mappa visiva che aiuta a identificare tendenze, anomalie o semplicemente a comprendere meglio una relazione tra due variabili.

Ad esempio, immaginate di voler visualizzare come varia la distanza percorsa da un oggetto rispetto al tempo impiegato. Sul piano cartesiano, il tempo potrebbe essere rappresentato sull’asse x mentre la distanza sull’asse y. Il risultato sarebbe un grafico che mostra chiaramente l’andamento della distanza in funzione del tempo.

Scopriamo insieme come funziona!

• Visualizzazione della raccolta dati in fisica
• Proporzionalità tra grandezze
• Come rappresentare dati sul piano cartesiano in fisica

Visualizzazione della raccolta dati in fisica

L’arte dei dati: come possiamo visualizzare le misure?

Abbiamo raccolto i dati: scelto il fenomeno, il sistema di misura e gli strumenti di misurazione, abbiamo ottenuto una corposa serie di numeri che ci dicono quanto tempo impieghi il pianoforte a cadere dal terrazzo, o che traiettoria segua il giavellotto lanciato dall’atleta.
Il cronometro ci ha misurato il tempo, il metro ci ha restituito la lunghezza, il tachimetro ci ha fotografato la velocità. Siamo certi delle nostre misure, naturalmente a meno della loro incertezza.

Occorre trovare il modo di visualizzare questa misura: visualizzare, dipingere, creare un grafico dà un’idea precisa e immediata di quale forma abbiano i dati e quali siano le relazioni in gioco tra i dati stessi… Ci permette di capire se queste relazioni esistono, se le nostre misure hanno un senso, se abbiamo investigato un fenomeno adeguato e se l’abbiamo fatto in modo adeguato.

Il Piano Cartesiano: il matrimonio tra algebra e geometria
Il modo più semplice e immediato di visualizzare i dati è attraverso il Sistema di Riferimento Cartesiano, detto Piano Cartesiano nella sua rappresentazione più semplice, quella bidimensionale tracciabile con la massima facilità su un foglio o su una lavagna.
René Descartes (Cartesio, 1596-1650) compie il passo concettuale e grafico importantissimo di sposare algebra e geometria, numeri e figure, fornendo alle misure fisiche uno strumento semplice e potente per valutarne la loro correttezza, e per individuarne le relazioni.

Esempio: caduta del pianoforte dal terrazzo

Abbiamo osservato con attenzione la caduta del pianoforte da un terrazzo. Abbiamo accuratamente cronometrato il fenomeno facendo partire il cronometro quando il pianoforte comincia la sua caduta e, secondo per secondo prima del rovinoso impatto al suolo, abbiamo segnato la posizione alla quale il pianoforte si trova, e abbiamo segnato la velocità che il pianoforte acquisisce.

Abbiamo ora coppie di misure di velocità e tempi, e coppie di misure di posizioni e tempi: ogni secondo è il nostro punto di riferimento, al quale associamo la velocità di passaggio del pianoforte e la sua posizione.

La nostra serie di misure di riferimento, il tempo (£$t$£), espresso in secondi (£$s$£), è la variabile indipendente e si posiziona sull’asse orizzontale del Piano Cartesiano, l’asse delle ascisse.
Scegliamo di visualizzare la posizione (£$z$£) a cui il pianoforte si trova secondo per secondo: espressa in metri (£$m$£), la posizione sarà sull’asse verticale del piano cartesiano, l’asse delle ordinate. Ad ogni secondo, la caduta del pianoforte implica una posizione diversa e la posizione del pianoforte è, nel nostro esperimento, la variabile dipendente nel fenomeno osservato.

Cosa ci dice un grafico tempo-posizione (£$t,z$£) che fotografa la caduta di un pianoforte? Beh, ci mostra che a tempi maggiori si raggiungono più velocemente posizioni più avanzate: il moto, dapprima più lento, diviene più veloce e, unendo le diverse coppie di punti (£$t_i$£, £$z_i$£, dove £$i$£ è il numero delle nostre misure), otteniamo una linea che si curva verso l’alto.

Le altre coppie di misure confermeranno questa velocizzazione del moto, ossia questa accelerazione? Ce lo facciamo indicare da un nuovo grafico su un Piano Cartesiano, nel quale indichiamo il tempo (£$t$£) in secondi (£$s$£) sull’asse delle ascisse e le velocità (£$v$£) in metri al secondo (£$m/s$£) sull’asse delle ordinate: di nuovo il tempo sarà la variabile indipendente, e la velocità sarà la variabile dipendente. Bene, tracciamo la curva che unisce i punti (£$t_i$£, £$v_i$£) e osserviamo… che non è una curva, nel senso più colloquiale del termine: è una retta. A tempi maggiori corrispondono velocità maggiori: esiste quindi un’accelerazione costante del moto.

Due bei grafici per una rumorosa distruzione: che cosa ci insegna il sacrificio del pianoforte?
Le coppie di misure hanno permesso la visualizzazione semplice del fenomeno di caduta e il riconoscimento dell’accelerazione uniforme di questo moto verticale.
Se abbiamo preso i dati bene, ossia se abbiamo cercato di minimizzare gli errori e le inevitabili incertezze, il Piano Cartesiano risponde mostrandoci una relazione fisica comprensibile: in questo fenomeno la posizione è variabile dipendente del tempo, e osservo una relazione lineare (osservo una linea retta) tra il tempo e la velocità della caduta.

La geometria analitica ci insegna come interpretare la forma di queste relazioni fisiche e la meccanica si prenderà cura di spiegare le equazioni del moto rovinoso di un pianoforte, ma è il Piano Cartesiano che ci ha permesso di vedere queste relazioni fisiche, ed è la scelta del fenomeno e la sua misurazione che ci hanno permesso di tracciarle.

Proporzionalità tra grandezze

Alcune grandezze sono dipendenti da altre. Questo perchè certe grandezze sono regolate da proporzionalità diretta o inversa, a volte alcune possono trovarsi in proporzione con il quadrato di altre grandezze!

Il modo migliore per rappresentarle è sicuramente utilizzare il grafico cartesiano.

Facciamo alcuni esempi:

1. La velocità (£$\vec{v}$£) in un moto rettilineo uniforme si trova dividendo lo spazio percorso (£$s$£) e il tempo impiegato (£$t$£). Quindi, con la velocità costante, spazio e tempo sono direttamente proporzionali: £$\frac{S}{t}$£ = £$v$£. Se un corpo viaggia con velocità costante £$10 \ \frac{m}{s}$£ il rapporto tra lo spazio percorso e il tempo impiegato sarà costante, al raddoppiare di una grandezza raddoppierà anche l’altra.
2. Se lo spazio è costante, allora £$t$£ e £$v$£ sarebbero inversamente proporzionali: al raddoppiare della velocità il tempo impiegato dimezza e viceversa.
3. Nel moto rettilineo uniformemente accelerato quando la velocità iniziale è uguale a 0, £$S$£ = £$\frac{at^2}{2}$£ , quindi lo spazio è direttamente proporzionale al tempo al quadrato (proporzionalità quadratica).

Come rappresentare dati sul piano cartesiano in fisica

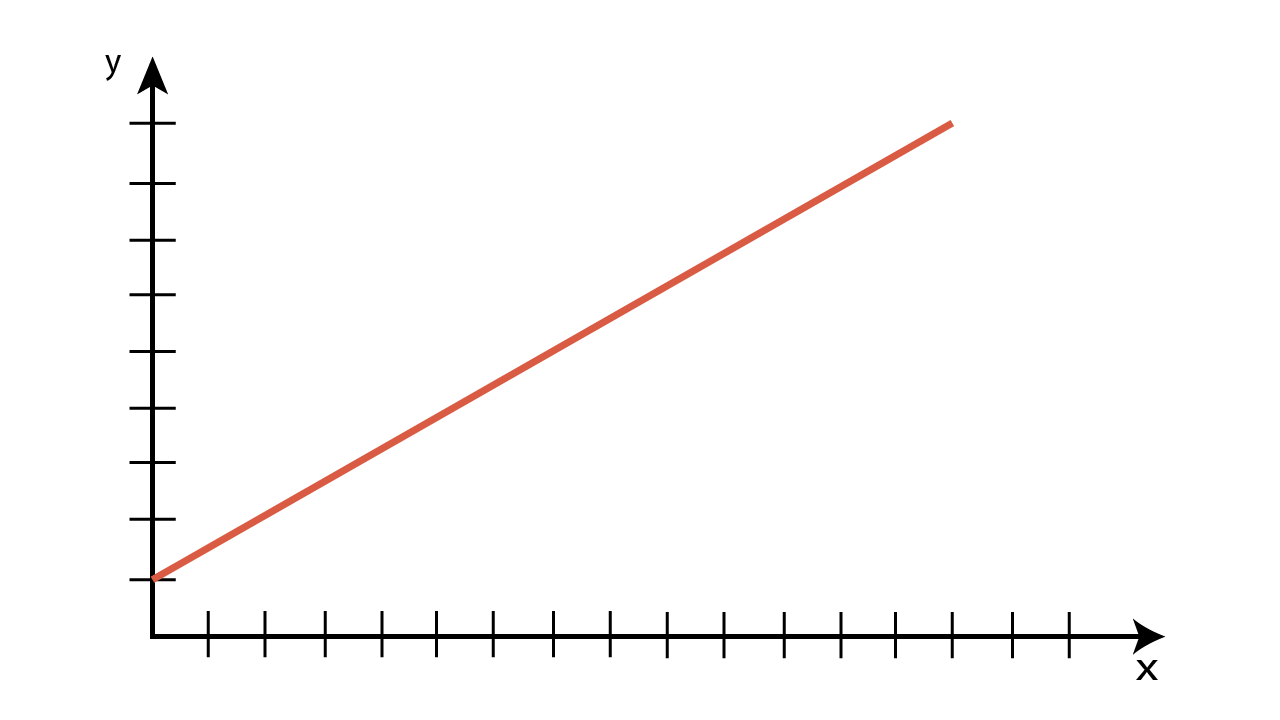
Ora proviamo a rappresentare questi dati sul piano cartesiano.

Nel 1° caso, se mettiamo la variabile indipendente (£$t$£) sull’asse delle ascisse, e lo spazio (£$s$£) sull’asse delle ordinate il risultato sarà una retta.

Quando tra due grandezze c’è proporzionalità diretta sul grafico cartesiano si forma una retta:

• passante per l’origine se lo spazio iniziale (£$S_i$£) è uguale a 0
• che interseca l’asse delle ordinate nel punto (0; £$S_i$£) se £$S_i$£ ≠ 0

Quando tra due grandezze c’è proporzionalità inversa (come nel 2° caso) il risultato è un ramo di iperbole equilatera.

Quando una grandezza è proporzionale al quadrato di un’altra (3° caso) si forma un ramo di parabola.

Il piano cartesiano, inoltre, può anche rappresentare il movimento di un punto materiale, mettendo sull’asse delle x le ascisse e sull’asse delle y le ordinate. La linea rappresentata su questo grafico spazio-spazio sarà la traiettoria del nostro punto materiale.