Il modello atomico di Bohr: definizione ed esempi

La nostra comprensione dell’atomo, la minuta unità fondamentale della materia, ha subito una serie di rivoluzioni nel corso della storia della scienza. Dalle prime teorie filosofiche dell’antichità, che ipotizzavano l’esistenza di particelle indivisibili che compongono la materia, fino alle complesse teorie quantistiche del XX secolo, la nostra visione dell’atomo ha subito cambiamenti radicali.

Tra questi cambiamenti, uno dei più significativi e influenti è stato senza dubbio il modello atomico proposto da Niels Bohr all’inizio del 20° secolo. Prima di Bohr, l’atomo era spesso immaginato come una sorta di “budino di prugne", con elettroni incastonati in una sfera di carica positiva. Tuttavia, questo modello non riusciva a spiegare una serie di fenomeni osservati, in particolare le linee spettrali degli atomi quando erano eccitati.

Fu Bohr a fornire una spiegazione coerente, introducendo concetti rivoluzionari che combinavano intuizioni della fisica classica con emergenti idee della quantizzazione. Il suo modello atomico non solo ha gettato le basi per la futura ricerca in fisica quantistica, ma ha anche rappresentato un momento chiave nella nostra crescente comprensione della natura fondamentale della realtà: scopriamo come!

• Il modello atomico planetario
• Le ipotesi di Bohr
• La condizione di quantizzazione di Bohr
• I raggi delle orbite e i livelli energetici nel modello di Bohr
• L’atomo legato secondo il modello di Bohr

Il modello atomico planetario

Il modello planetario prevedeva che gli elettroni orbitassero lungo una circonferenza attorno ad un nucleo di carica positiva con una certa accelerazione centripeta. Dall’elettromagnetismo(LINK) sappiamo, però, che una carica in moto emette sempre energia sottoforma di onde elettromagnetiche, come la luce. Queste emissioni avrebbero dovuto far perdere energia agli elettroni portandoli a “decelerare" e quindi a collassare verso il nucleo atomico in un tempo dell’ordine di £$10^{-7} \ s$£!

Ciò che si notava nella realtà è che gli atomi erano sistemi stabili e sicuramente non si distruggevano in un decimo di milionesimo di secondo. Perciò Bohr suppose che le leggi classiche della meccanica e dell’elettromagnetismo non valessero a livello atomico.

C’era bisogno di introdurre un nuovo modello della struttura atomica.

Le ipotesi di Bohr

Per risolvere le incongruenze del sistema atomico planetario, Bohr propose delle ipotesi che prevedessero la stabilità degli atomi per cui:

• il raggio dell’orbita di un elettrone attorno al nucleo può assumere solo un insieme di valori permessi
• se l’elettrone percorre un’orbita di raggio permesso, non irradia.

Si suppose che l’orbita di un elettrone attorno ad un nucleo, come la sua carica, fosse quantizzata. Queste ipotesi furono usate da Bohr come modello di studio per l’atomo di idrogeno anche se non erano ancora chiaramente dimostrabili.

Nel modello atomico di Bohr, il raggio, la velocità dell’elettrone e la sua energia totale potevano assumere solo un insieme di valori discreti e definiti, cioè erano quantizzate.

La condizione di quantizzazione di Bohr

Bohr concentrò i suoi studi sull’atomo di idrogeno, l’atomo più facile da analizzare perché ha solo un elettrone; inoltre, suppose che l’orbita percorsa dalla particella carica negativamente fosse circolare.

La condizione di quantizzazione che Bohr ottenne per l’atomo di idrogeno è espressa dalla formula: £$2 \pi \ r_n \ p_n=n \ h$£.

In cui £$n$£ è un qualsiasi numero intero positivo chiamato numero quantico principale, £$r_n$£ è il raggio dell’orbita £$n$£-esima dell’elettrone e £$p_n$£ è la corrispondente quantità di moto.

La condizione di quantizzazione determina le orbite quantizzate dell’elettrone permesse nell’atomo di idrogeno le loro caratteristiche principali, il raggio e la quantità di moto.

I raggi delle orbite e i livelli energetici nel modello di Bohr

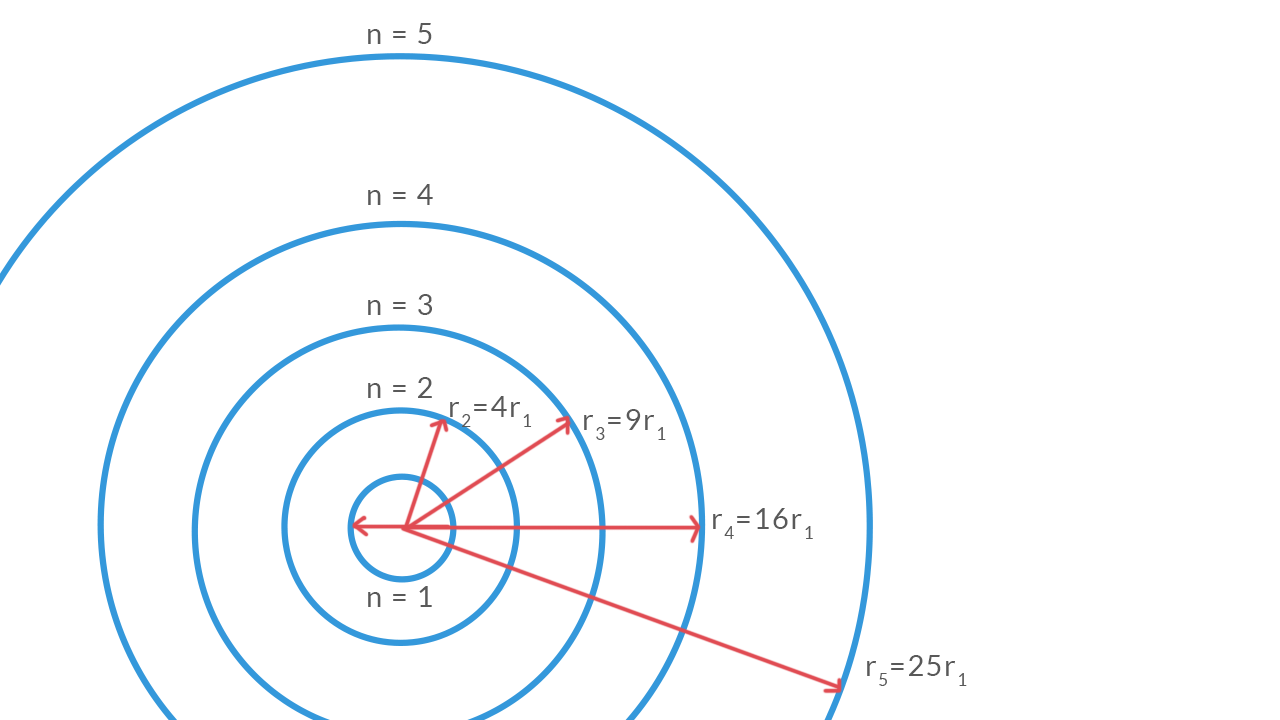
Dalla condizione di quantizzazione di Bohr possiamo ottenere l’equazione che fornisce i raggi delle orbite permesse nell’atomo di idrogeno:

£$r_n= \frac {\mathcal{E}_0 \ h^2}{\pi \ m_e \ e^2} \ n^2$£

Possiamo notare che il fattore £$\frac {\mathcal{E}_0 \ h^2}{\pi \ m_e \ e^2}$£ è un insieme di costanti, la costante dielettrica del vuoto, la costante di Planck, il pi greco, la massa dell’elettrone e la sua carica al quadrato, perciò ha un valore definito di £$5,29 \cdot 10^{-11} m$£. Dato che la formula assume questo valore per £$n=1$£, (£$5,29 \cdot 10^{-11} m$£) è anche il valore più piccolo che il raggio orbitale dell’elettrone dell’idrogeno può assumere ed è chiamato raggio di Bohr.

Per £$n$£ maggiori di 1 si ottengono i raggi delle orbite successive e più esterne.

Sappiamo dall’esperienza e dalle osservazioni di Bohr sulla stabilità del sistema nucleo-elettrone che l’atomo è un sistema legato, cioè non può scindersi spontaneamente, serve fare lavoro esterno per dividerlo.

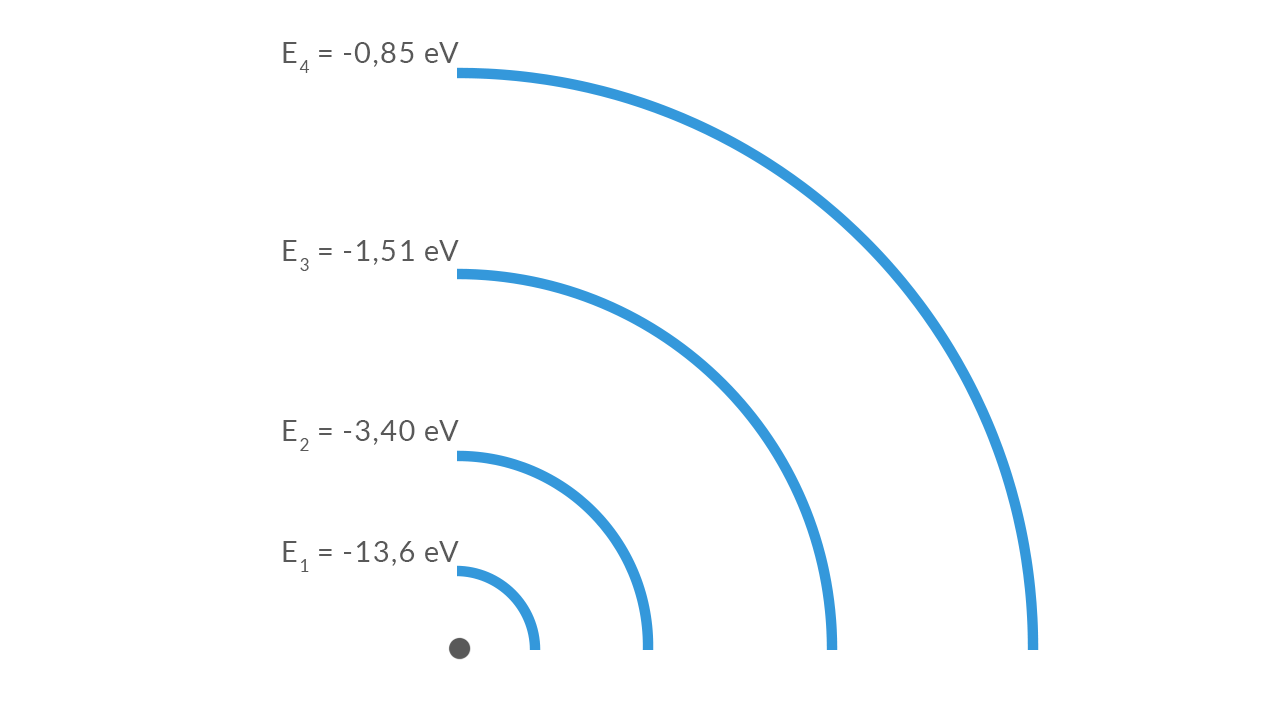
Si può dimostrare che l’energia totale del sistema nucleo-elettrone è: £$E_{tot}= – \frac {1}{8 \pi \mathcal{E}_0} \frac {e^2}{r}$£. Sostituendovi la formula del raggio quantizzato £$r_n$£, otteniamo i livelli energetici delle rispettive orbite £$n$£ : £$E_n=- \frac {m_e \ e^4}{8 \mathcal{E}_0^2 \ h^2}$£ che, riducendo le costanti presenti, diventa: £$E_n= -\frac {13,6 \ eV}{n^2}$£.

L’elettronvolt (£$eV$£) vale £$1,60 \cdot 10^{-19} \ J$£ e misura i livelli energetici degli atomi; per £$n=1$£ abbiamo il livello energetico fondamentale che vale £$-13,6 \ eV$£.

Possiamo dedurre dalla forma matematica di £$E_n$£ che i livelli energetici degli elettroni e quindi dell’atomo sono inversamente proporzionali a £$n^2$£ e quantizzati, infatti possono assumere solo valori interi e definiti.

L’atomo legato secondo il modello di Bohr

Diciamo che il sistema nucleo-elettrone è legato, ma cosa significa? Percé possiamo affermarlo?

Diciamo che il sistema nucleo-elettrone è legato perchè vediamo in natura che gli atomi non emettono elettroni all’impazzata, ma possono liberarli solo se sottoposti a lavoro, cioè energia.

Possiamo dire che l’energia di legame di un livello £$E_n$£ corrisponde al minimo lavoro necessario £$W_L$£ utile a estrarre un elettrone dalla sua orbita.

Il lavoro minimo che deve essere compiuto è uguale di modulo dell’energia di legame £$E_n$£, ma opposto di segno, cioè £$W_L=-E_n$£.

Considerato che il segno dell’energia di legame è sempre negativo (£$E_n= -\frac {13,6 \ eV}{n^2}$£), il lavoro per estrarre un elettrone dalla sua orbita è positivo, cioè diretto verso l’esterno del sistema e parallelo allo spostamento che viene imposto all’elettrone, mentre l’energia di legame ha segno opposto. Dato che le forze interne all’atomo sono positive e opposte al lavoro di estrazione, il sistema nucleo-elettrone deve essere legato.