L'ordine delle operazioni nelle espressioni matematiche
Le espressioni numeriche sono come frasi in un linguaggio: se non seguiamo le regole grammaticali, il significato può cambiare radicalmente. Uno degli aspetti cruciali per decifrare correttamente le espressioni matematiche è comprendere l’ordine in cui le operazioni devono essere eseguite. Allo stesso modo in cui la punteggiatura guida la nostra comprensione di una frase, l’ordine delle operazioni e delle parentesi ci indica come “leggere" e risolvere un’equazione o un’espressione.
Quante volte ci siamo chiesti: “Risolviamo prima la moltiplicazione o la somma? E quando dobbiamo calcolare ciò che sta all’interno delle parentesi?". Questi interrogativi non sono banali e, se affrontati senza una chiara comprensione delle regole, possono portare a risultati errati.
In questo articolo, faremo chiarezza su questi principi fondamentali. Potrai imparare insieme a noi qual è l’ordine delle operazioni ma anche qual è l’ordine delle parentesi che dovrai risolvere e, vedrai, le espressioni saranno un gioco da ragazzi!
Vuoi testare la tua preparazione? Prova il nostro quiz!
- Espressioni: catene di operazioni
- Le proprietà delle operazioni nelle espressioni
- L'ordine delle operazioni e delle parentesi nelle espressioni
- La regola PEMDAS per ricordare l'ordine delle operazioni
- La mappa mentale dell'ordine delle espressioni
Espressioni: catene di operazioni

Abbiamo imparato a calcolare addizioni, sottrazioni, moltiplicazioni e divisioni.
Ma nella vita di tutti i giorni siamo abituati ad affrontare problemi più complessi, in cui è necessario risolvere più operazioni, una dopo l’altra: sono le espressioni.
Le proprietà delle operazioni nelle espressioni
Ripassiamo insieme le proprietà delle 4 operazioni:
- addizione: proprietà commutativa e proprietà associativa;
- sottrazione: proprietà invariantiva;
- moltiplicazione: proprietà commutativa, proprietà associativa e proprietà distributiva rispetto alla somma;
- divisione: proprietà invariantiva.
Due numeri particolari: lo 0 e l’1, come si comportano in tutte le operazioni?
Ricordati di tutte queste proprietà per imparare a risolvere velocemente le espressioni. Infatti, le proprietà delle operazioni restano le stesse anche all’interno delle espressioni!
Come si comportano lo 0 e l’1 nelle quattro operazioni nelle espressioni
Lo 0 è l’elemento neutro per l’addizione: infatti £$ 5 + 0 = 0 + 5 = 5 $£. La sottrazione invece non ha elemento neutro perché “funziona solo da una parte" (infatti per la sottrazione non vale la proprietà commutativa): £$ 5 – 0 = 5 $£, ma £$ 0 – 5 = … $£? Lo scopriremo studiando i numeri relativi!
L’1 è l’elemento neutro per la moltiplicazione: infatti £$ 5 \cdot 1 = 1 \cdot 5 = 5 $£. La divisione non ha elemento neutro perché “funziona solo da una parte" (infatti per la divisione non vale la proprietà commutativa): £$ 5 : 1 = 5 $£, ma £$ 1 : 5 = … $£? Lo scopriremo studiando le frazioni!
L’ordine delle operazioni e delle parentesi nelle espressioni

Come procedere per risolvere un’espressione? Quali operazioni hanno la precedenza?
Quando scriviamo un’espressione, dobbiamo individuare le moltiplicazioni e le divisioni: sono le prime operazioni da risolvere, nell’ordine in cui si presentano.
Risolte tutte le moltiplicazioni e le divisioni, passiamo a addizioni e sottrazione, risolvendole sempre nell’ordine in cui compaiono.
Riassumendo, per risolvere un’espressione dobbiamo calcolare:
- prima moltiplicazioni e divisioni;
- poi addizioni e sottrazioni.
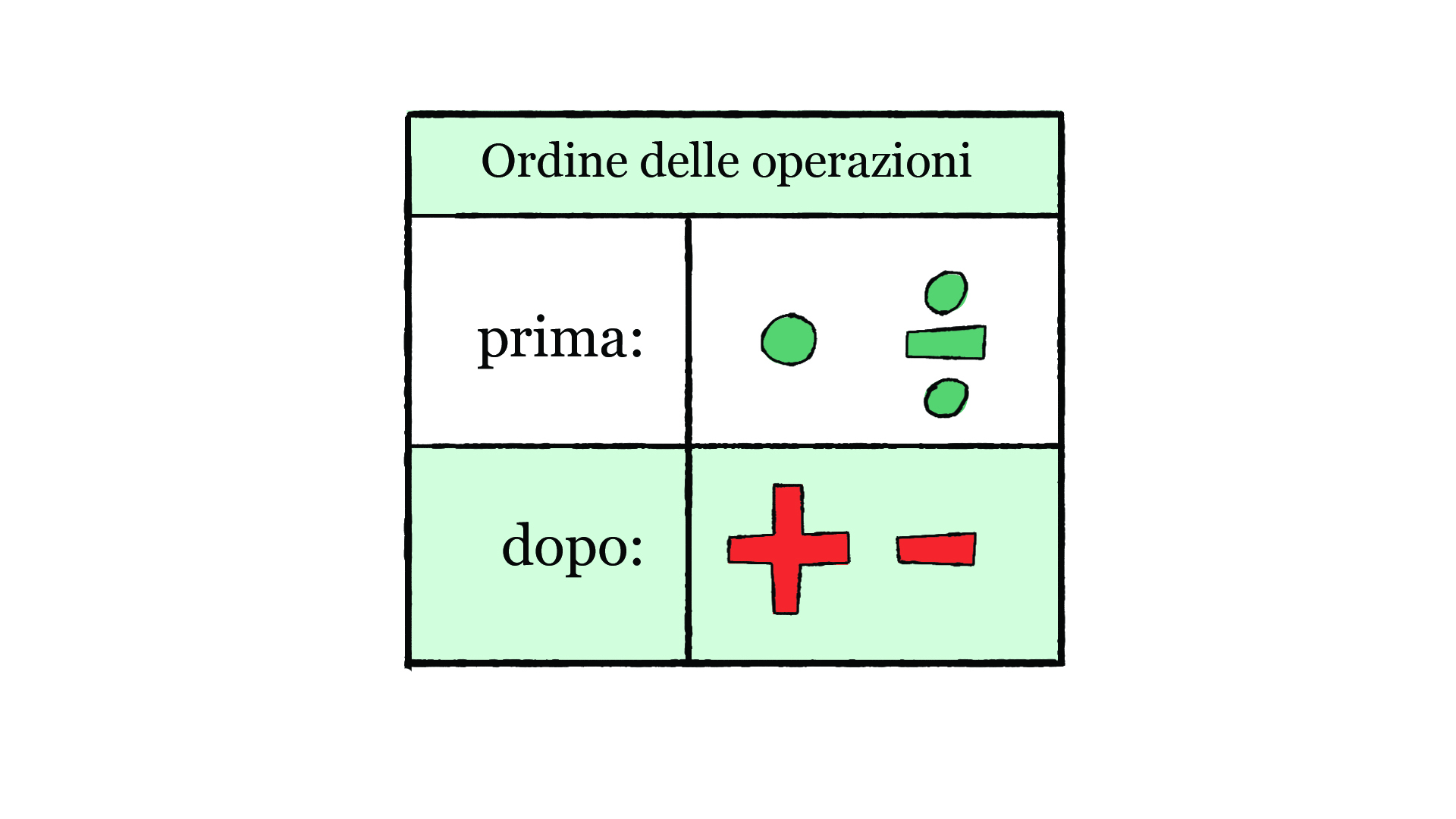
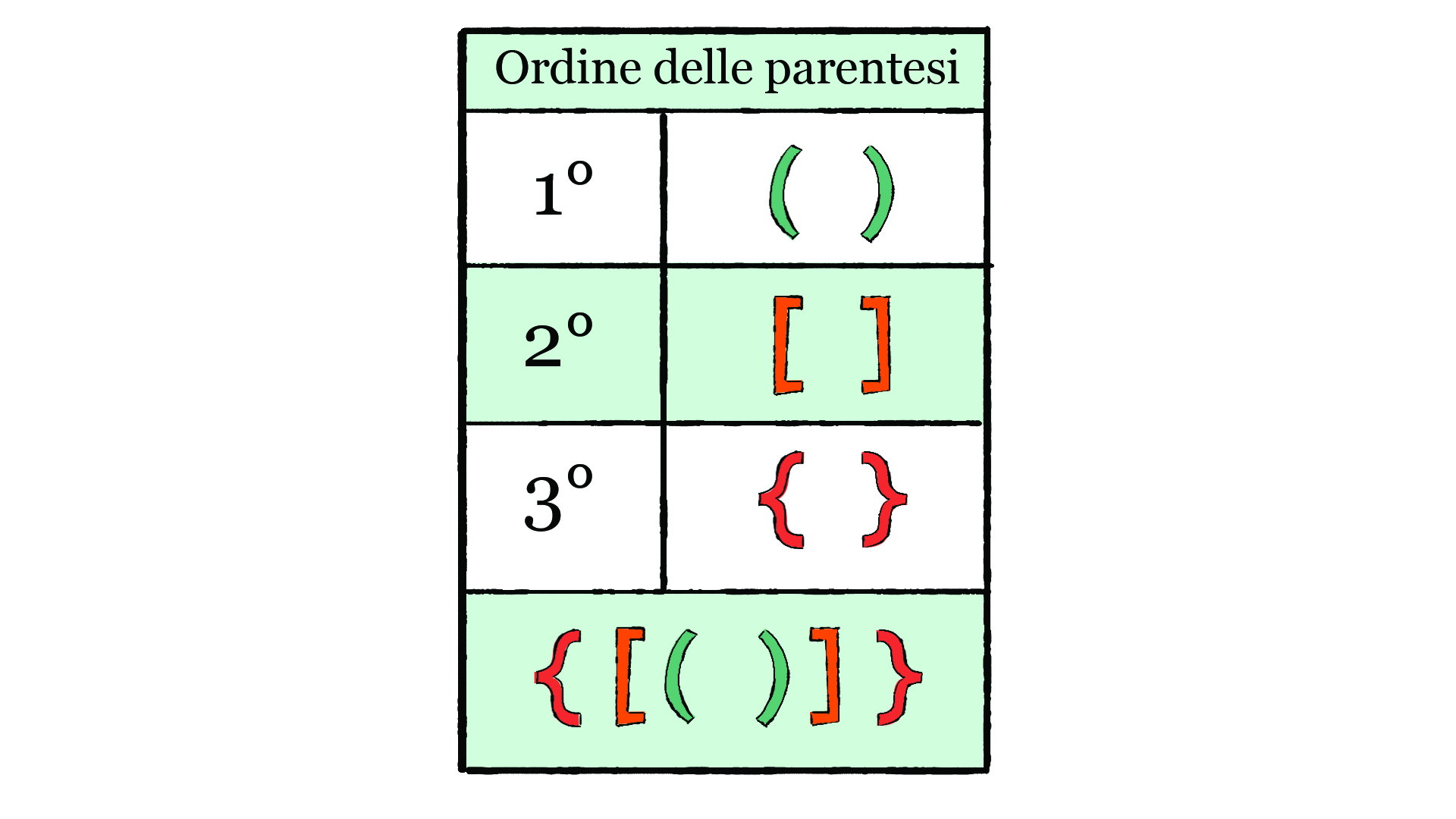
Per risolvere le espressioni, dobbiamo rispettare anche la priorità da dare alle parentesi. Se nell’espressione compaiono delle parentesi, seguiamo sempre lo stesso ordine delle operazioni, ma risolviamo prima tutte le operazioni nelle parentesi tonde, poi quelle nelle quadre e infine quelle nelle graffe.
Ricordati l’ordine delle operazioni: prima i puntini, poi i trattini!
Ricordati la priorità delle parentesi: tonde, quadre e graffe!
La regola PEMDAS per ricordare l’ordine delle operazioni
Quando ci troviamo davanti a una espressione matematica, è fondamentale svolgere le operazioni nell’ordine corretto per ottenere il risultato esatto. L’ordine delle operazioni può essere ricordato attraverso l’acronimo inglese “PEMDAS“, che sta per Parentesi, Esponenti, Moltiplicazione e Divisione (da svolgere da sinistra a destra) e, infine, Addizione e Sottrazione (anch’esse da svolgere da sinistra a destra).
- Parentesi: queste hanno la massima priorità. Qualsiasi operazione all’interno delle parentesi deve essere completata prima di procedere. E qui, c’è anche un ordine: le parentesi tonde “( )" vengono risolte per prime, seguite da parentesi quadre “[ ]" e poi da parentesi graffe “{ }".
- Esponenti: questi includono potenze e radici quadrate. Se nella tua espressione c’è un numero elevato a una potenza, questa operazione viene eseguita prima di moltiplicazioni, divisioni, addizioni o sottrazioni.
- Moltiplicazione e Divisione: una volta risolte parentesi ed esponenti, si passa alle moltiplicazioni e alle divisioni, svolgendole nell’ordine in cui appaiono da sinistra a destra.
- Addizione e Sottrazione: queste sono le ultime operazioni da eseguire, anche in questo caso nell’ordine in cui si presentano da sinistra a destra.
Ecco un esempio pratico:
4 x 3 + 12 : 2 – 7
Compaiono una moltiplicazione, un’addizione, una divisione e una sottrazione. Iniziamo a riscrivere l’espressione risolvendo la moltiplicazione e la divisione:
12 + 6 – 7
Ora è il momento di addizione e sottrazione! Risolviamole in ordine per trovare il risultato dell’espressione:
18 – 7 = 11
La mappa mentale dell’ordine delle espressioni
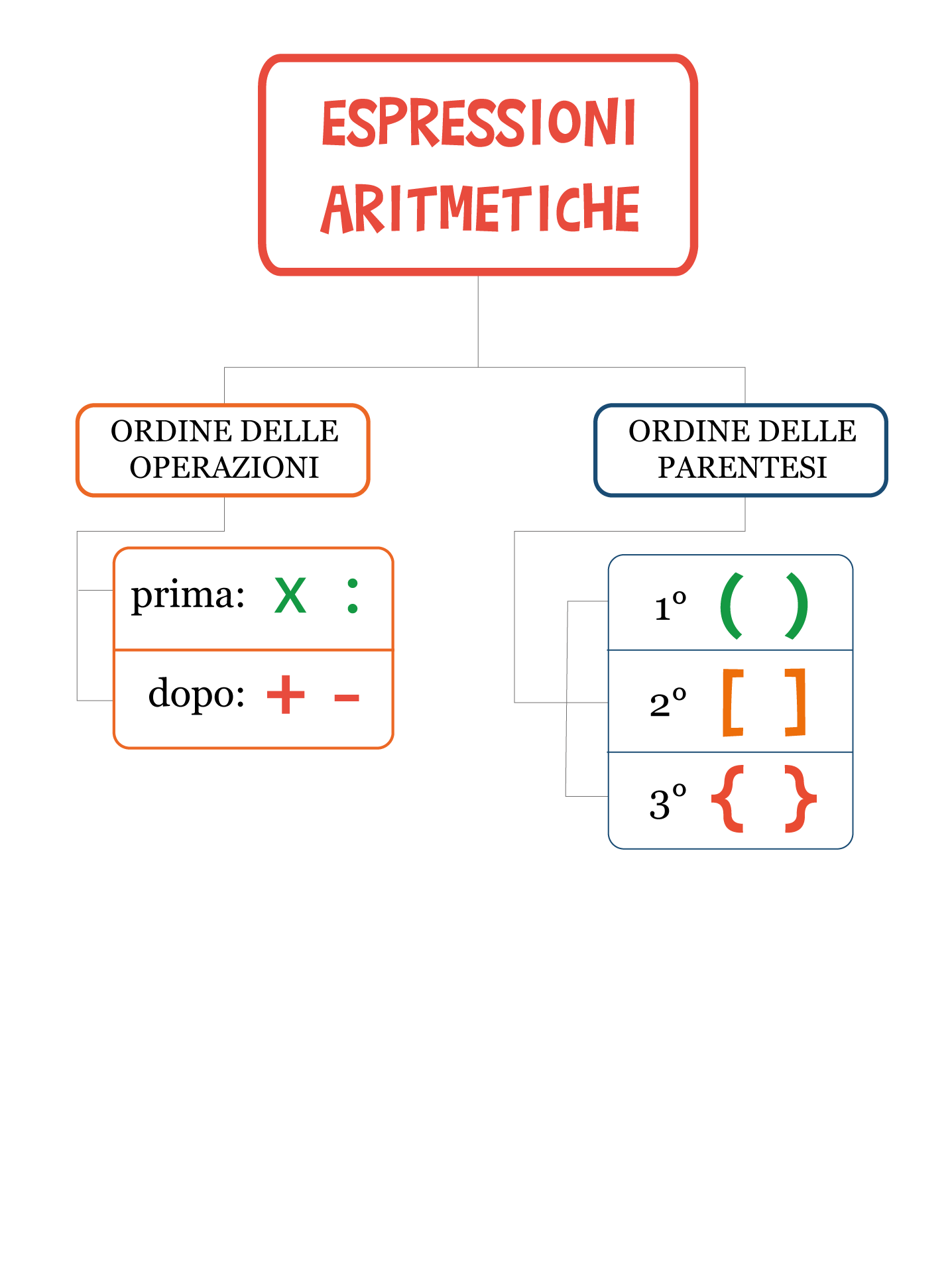
Come risolvere un’espressione?
Ripassa tutti gli argomenti sulle espressioni con l’aiuto della mappa mentale.
Scaricala e stampala per portarla sempre con te:
