L'esperimento di Millikan: la quantizzazione della carica

Tra gli esperimenti che hanno segnato la storia della fisica, pochi sono stati così importanti e illuminanti come l’esperimento di Millikan. Alla base di questo celebre esperimento, svoltosi nei primi anni del XX secolo, c’è la determinazione precisa di una delle costanti fondamentali della natura: la carica dell’elettrone. Ma, ancor più significativamente, i risultati di questo esperimento hanno rivelato una verità fondamentale sulla natura stessa della materia, ponendo le basi per la comprensione del concetto di quantizzazione.

In un periodo in cui la fisica stava vivendo una profonda rivoluzione, con teorie e idee che sfidavano la comprensione tradizionale del mondo, Robert Millikan si proponeva di sondare uno dei misteri più profondi dell’atomo: la natura e il valore della carica elettronica. Come poteva una particella così infinitamente piccola come l’elettrone avere una carica definita? E come poterla misurare con precisione?

L’esperimento di Millikan, noto anche come “esperimento della goccia d’olio“, non solo rispose a queste domande, ma rivelò anche un principio sorprendente: la carica non è un continuo, ma è “quantizzata", cioè può assumere solo certi valori discreti. Questa scoperta ha avuto implicazioni rivoluzionarie, suggerendo che il mondo microscopico obbedisce a leggi e principi radicalmente diversi da quelli del mondo macroscopico che percepiamo direttamente.

Scopriamo insieme di più sul suo esperimento!

• L'esperimento di Millikan
• L'analisi dell'esperimento di Millikan e la nascita della quantizzazione
• Le conclusioni di Millikan sulla quantizzazione

L’esperimento di Millikan

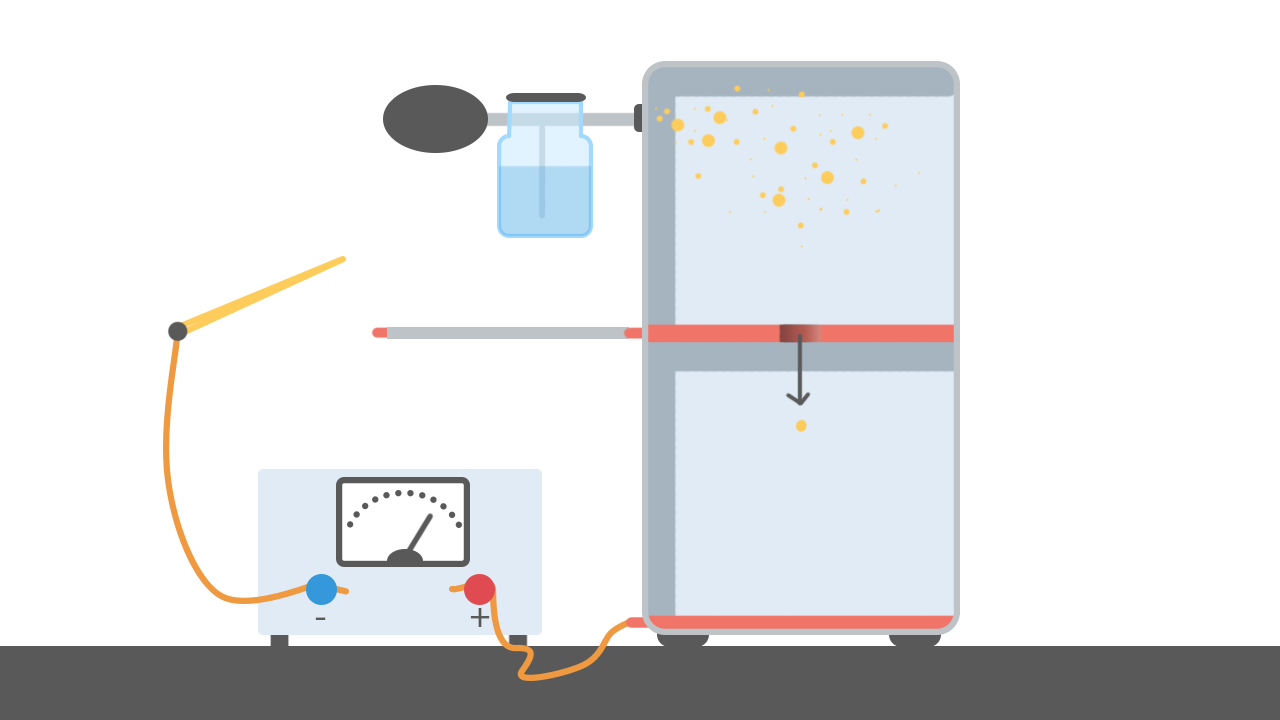
L’apparato sperimentale di Millikan era formato da:

• un nebulizzatore che spruzzava goccioline di olio in un comparto £$A$£; alcune di queste, per strofinio sul cannello, potevano acquisire una carica elettrica di qualsiasi segno
• alla base e a metà del contenitore erano posizionate due piastre collegate ad un circuito che fungevano da armature di un condensatore: sulla piastra superiore vi era un foro che permetteva il passaggio di piccole goccioline di olio dal comparto superiore £$A$£ al comparto inferiore £$C$£ compreso tra le armature del condensatore
• tra le armature si crea un campo elettrico uniforme di intensità £$E= \frac {\Delta V}{s}$£ dove, £$\Delta V$£ è la differenza di potenziale a cui sono sottoposte le armature e £$s$£ è la distanza tra di esse
• nel comparto £$C$£, compreso tra le armature del condensatore, abbiamo un microscopio che serve ad osservare le goccioline che si muovono nel campo elettrico creato nel comparto

Le goccioline uscite dal nebulizzatore cadevano nel comparto £$A$£ e, attraverso il foro nell’armatura superiore, entravano nel campo elettrico diretto verso l’alto generato dal condensatore nel comparto £$C$£. Finché il condensatore è scarico, si osserva al microscopio posizionato nel comparto £$C$£ che le goccioline si muovono verso il basso a velocità costante per via della forza peso e dell’attrito viscoso dell’aria.

Alla carica nel condensatore può accadere che:

• se la gocciolina è neutra, il suo moto resterà invariato
• se la gocciolina è carica positivamente, il suo moto tenderà a rallentare e a invertire il proprio verso sotto l’effetto della forza elettrica generata dal campo elettrico di verso opposto alla forza peso
• se la gocciolina è carica negativamente, il suo moto tenderà ad accelerare perché sottoposta ad una forza elettrica diretta nello stesso verso della forza peso

I casi in cui le goccioline sono cariche (il secondo e il terzo) si trattano nello stesso modo; noi, per comodità, esamineremo solo il secondo, con una gocciolina carica positivamente nel campo elettrico.

L’analisi dell’esperimento di Millikan e la nascita della quantizzazione

Millikan determinò i raggi delle goccioline grazie alle osservazioni al microscopio e, conoscendo la densità dell’olio, calcolò le loro masse.

Dopodiché si dedicò ad analizzare il moto di una gocciolina carica positivamente nel campo elettrico del comparto £$C$£ diretto verso l’alto.

La gocciolina in questione è sottoposta:

• alla forza peso £$F_p= m \cdot g$£
• alla forza d’attrito viscoso £$F_a= 6 \ \pi \ \eta \ r \ v$£
• alla forza elettrica £$F_e= q \cdot E= q \frac{\Delta V}{s}$£

Si osservò sperimentalmente che la gocciolina si muoveva di moto rettilineo uniforme che, tradotto secondo il primo principio della dinamica, significava che la somma vettoriale delle forze ad essa applicate doveva essere nulla.

Uguagliando le forze applicate sulla gocciolina si ha:

£$F_e=F_a+F_p$£ £$q \frac{\Delta V}{s}=6 \ \pi \ \eta \ r \ v + m \cdot g$£

da cui possiamo ricavare la formula per calcolare la carica della gocciolina: £$q=(6 \ \pi \ \eta \ r \ v + m \cdot g)\frac{s}{\Delta V}$£

Per calcolare la carica della gocciolina, Millikan doveva prima conoscere la sua velocità, per questo aveva dotato il microscopio di un reticolo che permetteva di calcolare lo spazio da essa percorso in un tempo £$t$£, da cui ricavare la sua £$v$£.

Il procedimento è analogo al caso in cui la carica sia negativa, fatto l’opportuno cambio di verso del vettore forza elettrica.

Le conclusioni di Millikan sulla quantizzazione

Dopo moltissime misurazioni e ripetizioni dell’esperimento fatte nell’arco di circa 4 anni, Millikan giunse ad una conclusione fondamentale: la carica elettrica è quantizzata, cioè assume solo valori interi e discreti, multipli di un valore fondamentale £$e=-1,6022 \cdot 10^{-19} C$£ che, in accordo con i modelli atomici proposti a inizio Novecento, non poteva che essere la carica di un elettrone. Infatti, in un atomo, solo gli elettroni possono spostarsi da un corpo ad un altro permettendo di determinarne la carica in base ad un loro eccesso o ad un loro difetto.

Si notava che il valore della carica era indipendente dal fatto che fosse positiva o negativa e che essa poteva assumere solo valori £$n$£ volte la carica fondamentale £$e$£.

Il risultato ottenuto da Millikan fu una conferma fondamentale per i fisici di inizio Novecento perché dimostrò che la meccanica quantistica era la strada giusta da seguire.