La pressione dei fluidi: cos'è e quali sono le tipologie

Fluidi di diversa natura avranno proprietà diverse, prima tra tutte la densità, fluidi diversi si disporranno in maniera diversa, compatibilmente con la loro differenza di densità. In particolare, in questo articolo cercheremo proprio di capire come può variare la pressione dei fluidi e quali sono le sue caratteristiche!

• Pressione idrostatica
• Calcolo della pressione di un fluido
• Pressione assoluta e pressione relativa
• Pressione totale
• L'andamento della pressione nei fluidi
• Il gradiente di pressione nei fluidi
• Andamento della pressione dei fluidi in geometrie diverse
• Superfici isobare e fluidi di diversa natura

Pressione idrostatica

La pressione può essere fisicamente spiegata come la forza esercitata da un fluido sull’unità di superficie con cui è a contatto. Se volessimo determinarla nella sua totalità dovremmo conoscere tutti i termini di pressione che vanno a definire lo stato finale del fluido in analisi. Esistono termini di pressione legati alla velocità di un fluido, altri legati alla sua posizione, presenti anche in stato di quiete.

Nel caso della statica dei fluidi si può assumere che non esistano termini di pressione legati alla velocità considerando che si analizzano solo stati di quiete, di conseguenza per ottenere il valore di pressione di un fluido sarà necessario sapere a che pressione esso si trova originariamente e infine aggiungere l’eventuale componente idrostatica dovuta al fatto che esiste una colonna di fluido a gravare su di esso.

Calcolo della pressione di un fluido

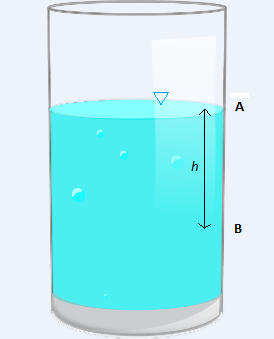
Osservando l’immagine possiamo capire come calcolare la pressione di una qualsiasi particella di fluido che si trova nel contenitore rappresentato. Il fluido che giace sulla superficie a contatto con l’aria nella parte alta, denominata “pelo libero", è in equilibrio con essa, il che significa che deve avere una pressione uguale a quest’ultima.

È possibile quindi assumere che nel punto A il fluido sia alla pressione atmosferica. Man mano che si procede in profondità la pressione delle particelle di fluido che si incontrano sarà sempre maggiore, compatibilmente con quanto enunciato dalla legge di Stevino. La componente di pressione idrostatica che cresce procedendo verso il fondo del contenitore andrà sommata al valore di pressione atmosferica a cui si trova il fluido già sul pelo libero.

Se volessimo quindi calcolare la pressione che ha una particella di fluido nel punto B dovremmo partire dal valore di pressione atmosferica che qualsiasi particella avrebbe se si trovasse nel punto A e, solo dopo, aggiungere la pressione idrostatica dovuta alla profondità tra il punto A e il punto B, calcolabile tramite la legge di Stevino.

Pressione assoluta e pressione relativa

Al fine di semplificare il modo in cui la pressione di un fluido viene espressa, si usa distinguere la componente di pressione atmosferica dal resto della pressione di un fluido. Con il termine pressione assoluta si indica la pressione che in generale un fluido ha, la pressione relativa è invece la componente di pressione che un fluido ha in più rispetto a quella atmosferica. Se ad esempio un fluido ha una pressione di £$10 Atm$£, si può indicare con £$10 Atm$£ la sua pressione assoluta, o in alternativa si può affermare che esso è a una pressione relativa di £$9 Atm$£. La pressione atmosferica equivale infatti ad £$1 Atm$£ dunque la sua pressione relativa di £$9 Atm$£, sommata a quella atmosferica di £$1 Atm$£, farebbe esattamente le £$10 Atm$£ di pressione a cui esso si trova. Per convenzione si usa aggiungere una “a" (dal termine inglese “absolute") all’unità di misura della pressione per specificare che ci si sta riferendo a una pressione assoluta e una “g" nel caso di pressione relativa (dall’inglese “gauge"). Per l’esempio appena considerato è quindi indifferente affermare che il fluido in questione sia a £$10 Atm_{a}$£ oppure a £$9Atm_{g}$£.

Pressione totale

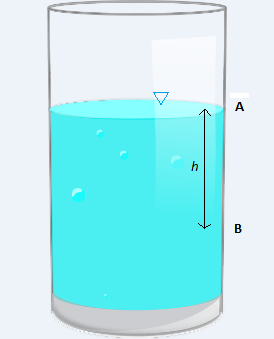
La pressione totale di un fluido sarà data dalla somma di tutte le componenti di pressione. La pressione totale del fluido che si trova alla profondità B sarà data dalla somma della pressione atmosferica e della pressione idrostatica data dalla profondità del punto B rispetto al pelo libero.

Nel punto A invece, dove la profondità a cui si trova il fluido è nulla, il valore di pressione totale sarà dato unicamente dal contributo della pressione atmosferica. La pressione idrostatica data dalla legge di Stevino nel punto A risulterebbe infatti nulla in quanto è pari a zero il termine h di profondità del punto A rispetto al pelo libero.

L’esperimento della bottiglietta di acqua forata

Ecco che siamo dunque in grado di spiegare perché nell’esperimento della bottiglia forata della lezione “La legge di Stevino" l’acqua non sarebbe in grado di uscire fino a che il tappo non viene rimosso: a bottiglietta chiusa la pressione atmosferica non insiste sull’acqua contenuta al suo interno mentre insiste dall’esterno sui fori che si sono creati sul lato della bottiglia. Come conseguenza di tutto ciò non c’è una forza a portare l’acqua a fuoriuscire, a meno che il tappo non venga rimosso e la pressione atmosferica torni a insistere anche sul pelo libero.

Cosa significa isobarico

Il termine isobarico significa “a pressione costante"; parlare di superfici isobare (o isobariche) significa dunque riferirsi a delle superfici che sono rappresentate dallo stesso valore di pressione in tutti i loro punti. Sapendo che la legge di Stevino afferma che l’andamento della pressione dei fluidi dipende dalla profondità, è intuitivo pensare che le superfici isobare siano caratterizzate da punti aventi in comune la medesima profondità rispetto al livello di fluido.

Nell’immagine possiamo dunque identificare più superfici isobariche caratterizzate dalla stessa profondità e di conseguenza dalla stessa pressione. La superficie isobarica C, trovandosi ad una maggiore profondità, avrà ovviamente una pressione maggiore della B, la quale a sua volta supererà il valore di pressione della superficie A.

L’andamento della pressione nei fluidi

La legge di Stevino può essere ben rappresentata graficamente utilizzando delle frecce. Ogni freccia ha una diversa lunghezza che indica il valore di pressione del fluido nel punto in cui essa è collocata. L’andamento crescente delle pressioni con la profondità risulterà quindi ben rappresentato da un triangolo in cui sono contenute delle frecce orizzontali di lunghezza maggiore man mano che si procede verso il basso.

Il gradiente di pressione nei fluidi

Per rappresentare l’andamento della pressione all’interno di un contenitore si usa solitamente disegnare un triangolo: esso racchiude delle frecce di lunghezza sempre maggiore indicando i valori di pressione che aumentano verso il basso.

Nella statica dei fluidi si usa quindi generalmente parlare di gradiente di pressione per indicare l’incremento graduale della pressione nel fluido man mano che si procede a profondità superiori.

Andamento della pressione dei fluidi in geometrie diverse

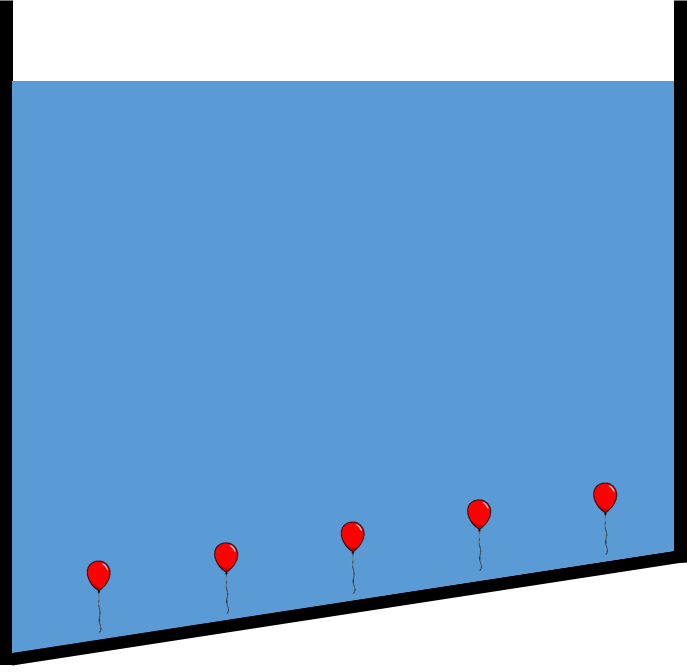
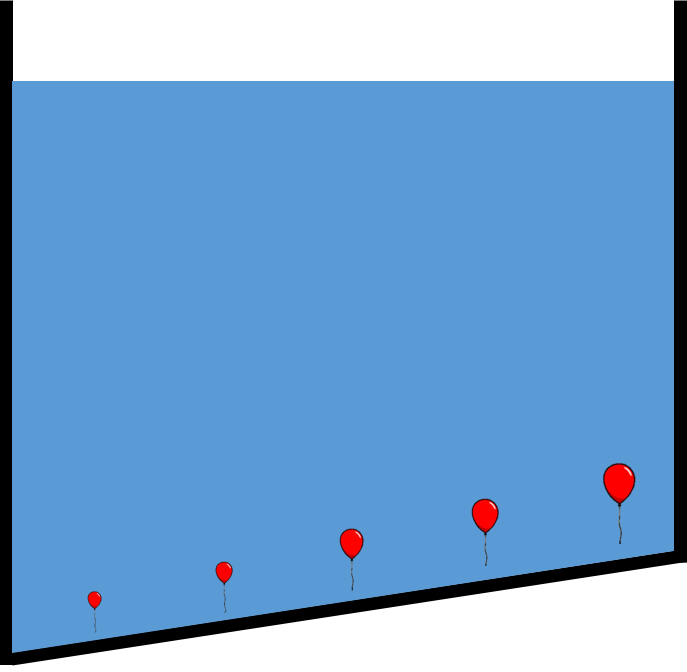
Proviamo a considerare il contenitore rappresentato in figura: se immaginassimo di disporre di nuovo dei palloncini sul fondo di quest’ultimo sarebbe corretto assumere che essi avranno tutti la stessa grandezza in quanto giacenti su di una superficie isobara?

La risposta è NO. Le superfici isobare si dispongono infatti sempre parallelamente al pelo libero del fluido, di conseguenza dei palloncini disposti lungo il fondo avrebbero idealmente dimensioni crescenti man mano che si procede da sinistra verso destra, ossia man mano che l’altezza h indicante la profondità a cui giace il palloncino si riduce.

Superfici isobare e fluidi di diversa natura

Immaginiamo ora di confrontare due recipienti contenenti fluidi di diversa natura. Ci aspettiamo che l’andamento delle pressioni con la profondità sia analogo? Assumere che a pari profondità h troveremo la stessa pressione p in entrambi i contenitori è corretto?
La risposta è NO. In entrambi i recipienti sarà rispettata la legge di Stevino e con essa l’andamento della pressione crescente con la profondità. Nonostante ciò però, dobbiamo ricordare che nell’espressione della legge di Stevino compare anche la densità del fluido. Se quindi confrontiamo due fluidi con diverse densità a profondità uguali non potremo incontrare gli stessi valori di pressione.
Ricordiamo brevemente la legge di Stevino:

£$p=\varrho gh$£

Essendo la pressione direttamente proporzionale alla densità, a pari profondità h otterremo in qualsiasi punto un valore di pressione £$p_{1}$£ maggiore di £$p_{2}$£ in quanto il fluido sulla sinistra ha densità £$\varrho_{1} $£ maggiore di £$\varrho_{2}$£. La forma del triangolo che descrive l’andamento della pressione in funzione della profondità risulterà quindi diversa a seconda della densità del fluido considerato.