Le onde luminose: definizione e caratteristiche della luce
La luce, al confine tra il tangibile e l’intangibile, ha ispirato poeti, artisti e scienziati, portandoli a indagare e riflettere sulla sua natura e sulle sue proprietà. Ma cosa sono realmente le onde luminose e come interagiscono con l’universo che ci circonda?
In fisica, la luce è descritta come un’onda elettromagnetica, una combinazione sincronizzata di campi elettrici e magnetici oscillanti, che si propagano attraverso lo spazio. Queste onde non necessitano di un mezzo materiale per viaggiare, permettendo alla luce di raggiungere anche i luoghi più remoti dell’universo. Dalle sfumature dell’arcobaleno alla tecnologia delle telecomunicazioni, le onde luminose sono alla base di una miriade di fenomeni e applicazioni.
Le caratteristiche delle onde luminose, come la lunghezza d’onda, la frequenza e l’intensità, determinano le diverse proprietà della luce che percepiamo e utilizziamo. Ad esempio, la diversa lunghezza d’onda delle onde luminose è ciò che ci permette di distinguere i vari colori. Inoltre, la velocità con cui queste onde viaggiano, costante nel vuoto, ha dato vita alla teoria della relatività di Einstein.
Non solo, la dualità onda-particella della luce, che suggerisce che essa possa comportarsi sia come un’onda che come una particella, ha rivoluzionato il nostro modo di vedere e comprendere l’universo a livello quantistico. Cerchiamo di scoprire meglio, oggi, quali sono le caratteristiche di queste onde e, di conseguenza, della luce!
- Cosa sono le onde luminose
- Le caratteristiche della luce
- Sovrapposizione e interferenza della luce e delle onde luminose
- L’esperimento di Young
- La diffrazione della luce
Cosa sono le onde luminose
Le onde luminose sono fluttuazioni nel campo elettromagnetico che si propagano attraverso lo spazio. Rappresentano una forma di energia radiante e sono responsabili di ciò che l’occhio umano percepisce come luce. Queste onde sono uniche e affascinanti in molti aspetti, e di seguito esploreremo le loro caratteristiche principali:
- Natura elettromagnetica: una delle proprietà fondamentali delle onde luminose è la loro natura elettromagnetica. Sono composte da campi elettrici e magnetici perpendicolari tra loro, oscillanti in modo sincronizzato mentre si muovono attraverso lo spazio, che interagiscono l’uno con l’altro. L’energia trasportata da queste oscillazioni è ciò che percepiamo come luce.
- Spettro elettromagnetico: le onde luminose coprono una vasta gamma di frequenze, formando ciò che è noto come lo spettro elettromagnetico. Anche se l’occhio umano può percepire solo una piccola parte di questo spettro, chiamata luce visibile, esistono molte altre forme di radiazione elettromagnetica, come i raggi X, i raggi gamma, le onde radio e i raggi ultravioletti, per citarne alcuni.
- Velocità: nel vuoto, tutte le onde luminose viaggiano alla stessa velocità costante, conosciuta come la velocità della luce, che è di circa 3×108 metri al secondo. Questa incredibile velocità è stata un punto chiave nella formulazione della teoria della relatività di Einstein.
- Dualità onda-particella: una delle scoperte più rivoluzionarie della fisica moderna è che la luce ha una natura duale. Può comportarsi sia come un’onda che come una particella (fotone). Questo concetto ha giocato un ruolo cruciale nello sviluppo della meccanica quantistica.
- Interazione con la materia: quando le onde luminose incontrano un mezzo diverso dal vuoto, possono essere rifratte, riflesse, diffuse o assorbite. Queste interazioni sono alla base di numerosi fenomeni ottici, come la formazione dell’arcobaleno o la dispersione della luce attraverso un prisma.
Le caratteristiche della luce

Isaac Newton fu uno dei primi scienziati ad interessarsi ai fenomeni luminosi. Egli sosteneva che la luce fosse un insieme di corpuscoli molto piccoli e veloci, dunque credeva che la luce avesse una natura corpuscolare. Questa interpretazione era la più accreditata fino agli inizi dell’Ottocento.
Christiaan Huygens, fisico olandese, al contrario, può essere annoverato tra coloro che sostenevano l’ipotesi diametralmente opposta e molto meno “di moda" della natura ondulatoria della luce; questa interpretazione prevedeva che la luce si comportasse come un’onda.
A sostegno di quest’ultima teoria si schierò il fisico inglese Thomas Young, il quale realizzò un esperimento in cui riuscì ad osservare l’interferenza tra due raggi luminosi, un fenomeno possibile solo nel mondo delle onde!
Il dibattito diede origine a due grandi rami dell’ottica: l’ottica geometrica, che si occupava di fenomeni in cui la luce sembrava comportarsi come un insieme di corpuscoli, e l’ottica fisica (o ondulatoria), che studiava le situazioni in cui la luce sembrava comportarsi da onda.
Chi aveva veramente ragione?
In certa misura TUTTI E DUE! Esistono dei casi in cui la luce è in grado di mostrare la sua natura corpuscolare interagendo con la materia (bisogna sottolineare, però, che con il termine “corpuscolo" si intendeva una particella massiva piccola e veloce, non ancora i “pacchetti di energia" della fisica quantistica); in altre situazioni, invece, la radiazione luminosa si comporta esattamente come onda, vale a dire, è in grado di interferire e diffrangere.
Sovrapposizione e interferenza della luce e delle onde luminose
Trattandosi di un’onda, anche la luce è in grado di interferire.
Le condizioni affinché sia creata una figura d’interferenza sono molto particolari:
- è necessario che i fasci di luce emessi dalle sorgenti siano monocromatici (devono essere costituiti da una sola lunghezza d’onda e quindi caratterizzati dalla stessa frequenza)
- le sorgenti devono mantenere una relazione di fase costante (due sorgenti si dicono in fase quando emettono luce in modo coerente, cioè quando diffondono contemporaneamente due creste o due ventri).
Ciò che non cambia è la condizione per cui si ottiene interferenza costruttiva o interferenza distruttiva.
Si ha un’interferenza costruttiva quando la differenza di cammino dalle sorgenti è un multiplo intero della lunghezza d’onda :
£$l_1 – l_2 = m \lambda$£
Dove £$l_1$£ e £$l_2$£ sono le distanze dal punto di incontro tra le onde e le sorgenti.
Si ha un’interferenza distruttiva quando la differenza di cammino dalle sorgenti è un multiplo intero dispari di mezza lunghezza d’onda:
£$l_1 – l_2 = \frac{m}{2}\lambda$£
Non ti ricordi le condizioni di interferenza per le onde? Vai alla lezione su Le onde!
L’esperimento di Young
L’apparato sperimentale di Young
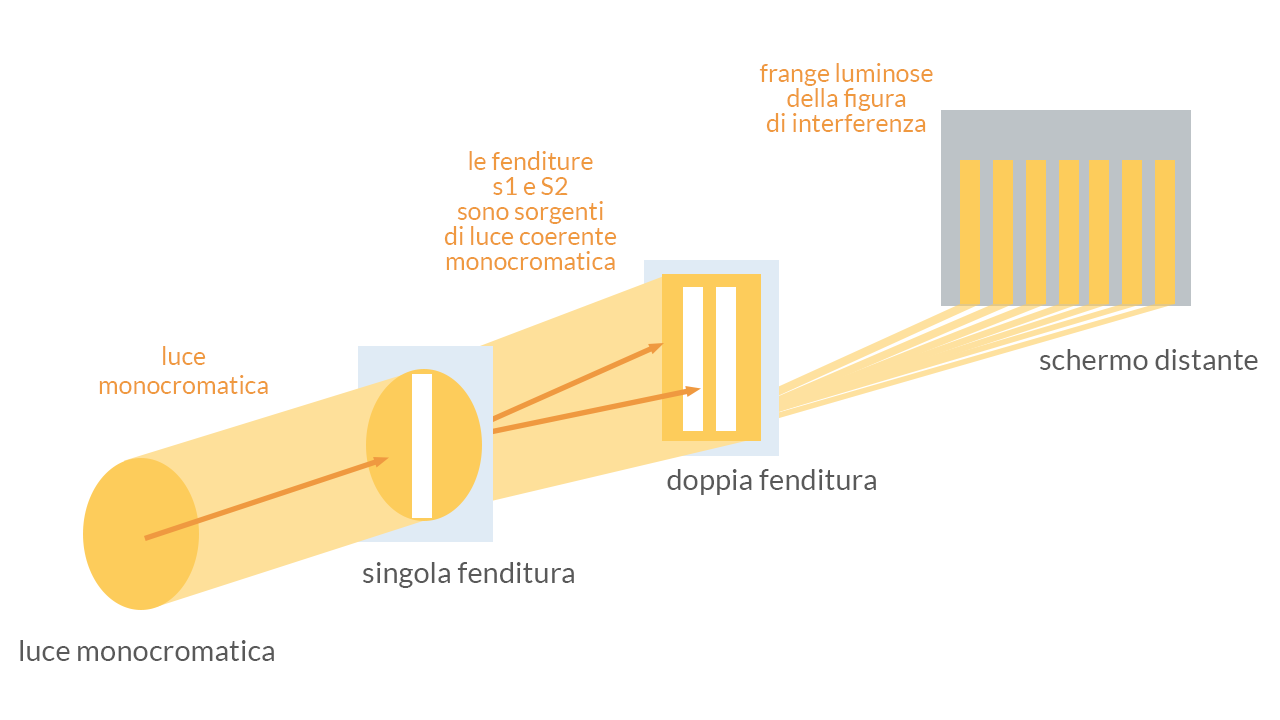
Le fenditure sono sorgenti puntiformi di onde

Intorno al 1801, il fisico inglese Thomas Young realizzò un esperimento che dimostrò la natura ondulatoria della luce.
Egli prese una sorgente di luce monocromatica e la puntò verso due schermi, posti l’uno dietro l’altro, il primo con una singola fenditura e il secondo con una doppia fenditura, come in figura 1.
Il raggio luminoso veniva proiettato sul primo schermo e, da lì, attraversa la fenditura, incideva sul secondo; infine, dalla doppia fenditura, la luce si propagava verso una parete sulla quale si presentò una figura di interferenza. Se la luce, come sosteneva Newton, fosse stata un insieme di corpuscoli, Young avrebbe dovuto vedere sulla parete solo due tratti illuminati in direzione della doppia fenditura ma questo non accadeva! L’unico modo possibile per spiegare i risultati ottenuti era interpretarli con la natura ondulatoria della luce!
Per realizzare questo esperimento il fisico inglese utilizzò uno dei principi proposti dal collega Christiaan Huygens : “ciascuna fenditura agisce come una sorgente di onde che si propagano verso l’esterno in tutte le direzioni" (le fenditure possono essere considerate come sorgenti puntiformi!).
Dunque, dato che le due fenditure poste sul secondo schermo si trovano alla stessa distanza rispetto alla prima, esse svolgono la funzione di sorgenti coerenti di luce.
Basandoci sugli studi di trigonometria e sulla figura collocata all’inizio del post, possiamo affermare che la differenza di cammino £$\Delta l$£ della luce proveniente dalle due fenditure è:
£$\Delta l = d \cdot sin \ \alpha$£
Di conseguenza, la frangia luminosa più vicina al punto centrale si verifica per un angolo £$\alpha$£ dato dalla condizione:
£$d \ sin \ \alpha = \lambda$£ £$sin \ \alpha = \frac{\lambda}{d}$£
La condizione affinché si crei una frangia luminosa (interferenza costruttiva) sulla parete è dunque:
£$d \ sin \ \alpha = m \lambda$£ (dove m=0,1,2 ecc.)
Mentre la condizione per le frange scure (interferenza distruttiva) risulta:
£$d \ sin \ \alpha = (m – \frac{1}{2}) \lambda$£
Se guardi attentamente la terza immagine, potrai capire anche quanto sia facile calcolare la distanza £$y$£ tra una frangia distante e quella centrale!
Usando la trigonometria, £$y$£ risulta:
£$y = L \ tg \ \alpha$£
La diffrazione della luce

Qualsiasi tipo di onda (onde del mare, onde sonore, onde luminose ecc.) sono in grado di diffrangere, ovvero possono cambiare disposizione dei fronti d’onda (le creste) quando incontrano un ostacolo.
Un esempio lampante consiste nella nostra possibilità di udire un suono nonostante non ci si trovi di fronte alla sorgente sonora che lo sta emettendo, come i giocatori di football americano sentono il quarterback chiamare gli schemi alle loro spalle.
Inoltre, secondo il principio di Huygens per cui ogni fenditura si comporta da sorgente puntiforme, quando le onde ne attraversano una, iniziano a diffondere in tutte le direzioni formando le cosiddette figure di diffrazione!
Analizziamo il caso più semplice, ovvero quello della diffrazione dovuta ad una singola fenditura.
La fenditura di larghezza £$W$£ svolge la funzione di sorgente puntiforme e crea, su una parete posta ad una distanza £$d$£ (molto maggiore di £$W$£), una figura di diffrazione. È importante sottolineare che la larghezza delle fenditure deve essere piccola perchè si possano avere figure di diffrazione, dell’ordine dei millimetri.
Come potete vedere dall’immagine, la frangia centrale, dove la differenza di cammino della luce dalle sorgenti (£$\frac{W}{2} sin \ \alpha $£) è 0, è sempre luminosa e la sua lunghezza risulta essere circa : £$2 \frac{\lambda}{W}$£.
Per la diffrazione, la condizione che permette di ottenere una frangia scura (interferenza distruttiva) è opposta a quella dell’interferenza:
£$W sin \ \alpha = m \lambda$£ (Dove m = 1,2,3 ecc.)
La formula appena descritta non vale per i reticoli di diffrazione, composti da una serie di fenditure poste l’una vicinissima all’altra (alcuni reticoli possono avere addirittura 40 000 fenditure per centimetro!), in grado far diffrangere il raggio luminoso che lo colpisce.
La figura d’interferenza che si crea è molto simile a quella che abbiamo visto in precedenza per l’esperimento di Young. Le frange luminose più evidenti, che rappresentano l’interferenza costruttiva, vengono chiamate massimi principali, intervallati da frange scure derivanti dall’interferenza distruttiva, e frange chiare molto più deboli, chiamate massimi secondari.
Ogni reticolo è caratterizzato dal numero di linee per unità di lunghezza £$N$£ che, solitamente, rappresenta il numero di fenditure del reticolo per centimetro.
La distanza £$d$£ tra le fenditure è semplicemente l’inverso di £$N$£.
Essendo simile a quanto già scritto nel post 3, possiamo dire che la condizione che deve essere soddisfatta per l’interferenza costruttiva è:
£$d \ sin \ \alpha = m \lambda$£ (Dove £$d$£ è la distanza tra una fenditura e quella successiva)
