Le operazioni tra i vettori: addizione e sottrazione

L’importanza dei vettori emerge in molte discipline scientifiche, dall’ingegneria all’aerodinamica, dalla fisica quantistica alla geometria. Mentre le semplici operazioni di addizione e sottrazione possono sembrare ovvie quando si tratta di numeri puri, nel contesto dei vettori esse acquisiscono una complessità diversa ed è necessario capire bene come affrontarle. Vediamo insieme come fare!

• Cosa sono i vettori
• Cosa sono la somma e la differenza tra vettori
• Come si eseguono analiticamente l’addizione e la sottrazione tra vettori
• Quali sono le proprietà dell’addizione e della sottrazione tra vettori
• Metodo del parallelogramma per l'addizione e la sottrazione con i vettori
• Metodo punta-coda per l'addizione tra vettori

Cosa sono i vettori

Un vettore è una quantità matematica caratterizzata da una grandezza e una direzione. Al contrario di uno scalare, che è definito solo dalla sua grandezza (come la temperatura o la massa), un vettore ha anche una direzione nello spazio. In termini grafici, un vettore è spesso rappresentato come una freccia, dove la lunghezza della freccia indica la grandezza del vettore e la direzione in cui punta la freccia rappresenta la direzione del vettore.

Ci sono alcuni concetti chiave da considerare quando si lavora con i vettori:

1. Punto di applicazione: è il punto in cui il vettore inizia.
2. Direzione: è l’orientamento dello spazio in cui il vettore agisce. Due vettori con la stessa grandezza ma direzioni opposte sono differenti.
3. Verso: indica la tendenza del vettore, che può essere positiva o negativa rispetto a un riferimento.
4. Modulo: è la grandezza o la lunghezza del vettore, spesso rappresentata dalla lunghezza della freccia in una rappresentazione grafica.

Quando si effettuano operazioni con vettori, come l’addizione e la sottrazione, è fondamentale tenere in considerazione tutti questi elementi. Ad esempio, l’addizione di due vettori richiede che si consideri sia la loro grandezza che la loro direzione e la somma risultante è un nuovo vettore che può avere una grandezza e una direzione completamente diverse dai vettori originali. Allo stesso modo, la sottrazione di vettori richiede un’attenzione particolare alla direzione e al modulo di ciascun vettore.

Cosa sono la somma e la differenza tra vettori

Se abbiamo due vettori £$\overrightarrow{v} = \overrightarrow{AB}$£ e £$\overrightarrow{w} = \overrightarrow{BC}$£, il vettore somma £$\overrightarrow{v} + \overrightarrow{w}$£ è dato dal segmento orientato che parte da £$A$£ e termina in £$C$£, oppure, equivalentemente, dalla diagonale £$\overrightarrow{AC}$£ del parallelogramma formato dai due vettori dati e dai due vettori ad essi equipollenti £$\overrightarrow{DC}$£ e £$\overrightarrow{AD}$£.

Il vettore differenza £$\overrightarrow{v} – \overrightarrow{w}$£ è invece dato dall’altra diagonale del parallelogramma, £$\overrightarrow{DB}$£.

Come si eseguono analiticamente l’addizione e la sottrazione tra vettori

Oltre all’interpretazione geometrica della somma e della differenza tra vettori, esiste anche una interpretazione analitica, che mette in relazione le componenti cartesiane del vettore somma e del vettore differenza con le componenti cartesiane dei vettori di partenza.

In un spazio cartesiano a N dimensioni, dati due vettori £$\overrightarrow{v} = (v_1, v_2, \dots, v_N)$£ e £$\overrightarrow{w} = (w_1, w_2, \dots, w_N)$£, il vettore somma è dato da da £$\overrightarrow{v} + \overrightarrow{w} = (v_1 + w_1, v_2 + w_2, \dots, v_N + w_N)$£. Analogamente, il vettore differenza è dato da £$\overrightarrow{v} – \overrightarrow{w} = (v_1 – w_1, v_2 – w_2, \dots, v_N – w_N)$£.

Quali sono le proprietà dell’addizione e della sottrazione tra vettori

L’addizione tra vettori gode delle seguenti proprietà:

• proprietà commutativa: £$\overrightarrow{u} + \overrightarrow{v} = \overrightarrow{v} + \overrightarrow{u}$£
• proprietà associativa: £$(\overrightarrow{u} + \overrightarrow{v}) + \overrightarrow{w} = \overrightarrow{u} + (\overrightarrow{v} + \overrightarrow{w})$£
• esistenza dell’elemento neutro: £$\overrightarrow{u} + \overrightarrow{0} = \overrightarrow{u}$£
• esistenza dell’elemento opposto: per ogni vettore £$\overrightarrow{v}$£ esiste il suo vettore opposto, che si indica con £$-\overrightarrow{v}$£, tale che £$\overrightarrow{v} +(-\overrightarrow{v}) = \overrightarrow{0}$£.

In particolare, il vettore nullo £$\overrightarrow{0}$£ è un vettore avente modulo uguale a zero.

Il vettore opposto è, come già visto, il vettore che ha uguale modulo, uguale direzione e verso opposto rispetto al vettore dato.

Una volta chiarito il concetto di vettore opposto, possiamo definire la differenza tra due vettori £$\overrightarrow{u}$£ e £$\overrightarrow{v}$£ come la somma tra il primo vettore £$\overrightarrow{u}$£ e l’opposto del secondo, £$– \overrightarrow{v}$£.

Metodo del parallelogramma per l’addizione e la sottrazione con i vettori

ADDIZIONE:

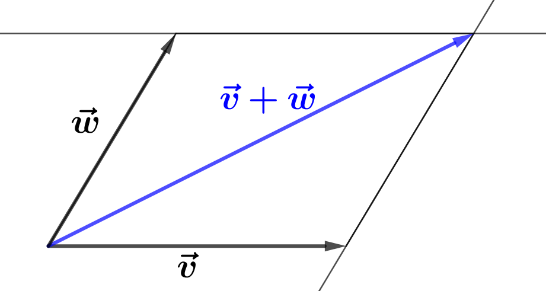
Si rappresentano i due vettori £$\overrightarrow{v}$£ e £$\overrightarrow{w}$£ in maniera tale che abbiano la coda coincidente. Si rappresenta il parallelogramma che ha come lati i due vettori, ovvero si traccia la parallela al vettore £$\overrightarrow{w}$£ passante per la punta di £$\overrightarrow{v}$£ e la parallela al vettore £$\overrightarrow{v}$£ passante per la punta di £$\overrightarrow{w}$£.

Si determina il punto di intersezione delle due parallele ai vettori e si traccia il vettore che ha la coda coincidente con la coda dei due vettori e la punta nel punto di intersezione appena determinato.

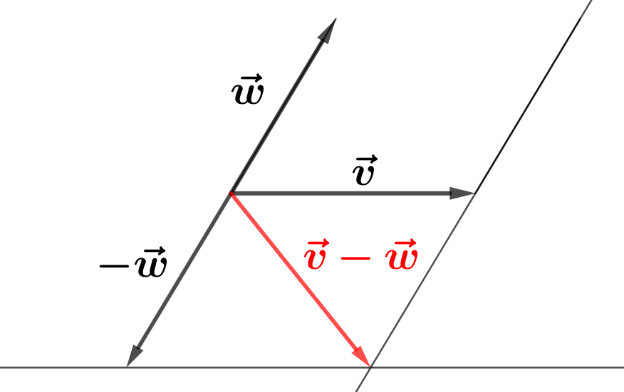
SOTTRAZIONE:

Si rappresentano i due vettori £$\overrightarrow{v}$£ e £$-\overrightarrow{w}$£, in maniera tale che abbiano la coda coincidente (il vettore £$-\overrightarrow{w}$£ ha lo stesso modulo e la stessa direzione del vettore £$\overrightarrow{w}$£, ma verso opposto). Si procede come nel caso dell’addizione.

Metodo punta-coda per l’addizione tra vettori

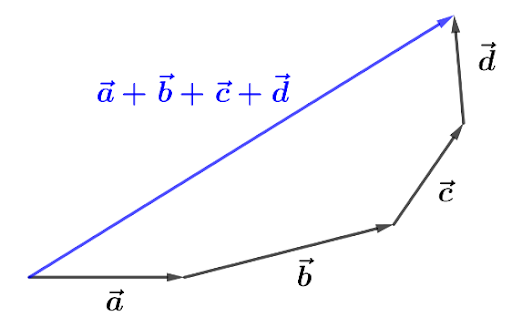
Si rappresentano i due vettori £$\overrightarrow{v}$£ e £$\overrightarrow{w}$£ in maniera tale che la punta del primo coincida con la coda del secondo. La somma £$\overrightarrow{v}$£ + £$\overrightarrow{w}$£ è data dal vettore che ha la coda in comune con il primo vettore e la punta in comune con il secondo vettore.

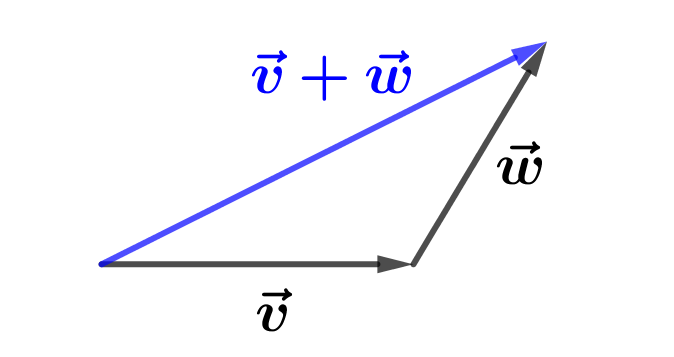
Questo metodo è utilizzato in particolare quando si deve eseguire la somma di più di due vettori.