Come disegnare il grafico di una funzione
La rappresentazione grafica di una funzione è una componente essenziale della matematica, fungendo da ponte tra l’astrazione numerica e la visualizzazione concreta. Questo processo trasforma le equazioni e le relazioni matematiche in immagini visive, permettendo una comprensione più immediata e intuitiva dei concetti matematici.
La rappresentazione grafica inizia identificando i valori chiave della funzione, come gli zeri (i punti dove la funzione interseca l’asse x), gli asintoti, i punti di massimo e minimo, e i punti di flesso. Questi elementi forniscono una “mappa" iniziale che guida la tracciatura del grafico. Nel caso di funzioni più complesse, l’analisi del comportamento asintotico e delle variazioni di concavità e convessità diventa fondamentale per una rappresentazione accurata.
In questo articolo, esploreremo in dettaglio il processo di rappresentazione grafica delle funzioni. Pronti? Cominciamo!
- Come scrivere una funzione
- I metodi per rappresentare graficamente una funzione
- Come riconoscere una funzione
Come scrivere una funzione
Abbiamo dato la definizione matematica di funzione, ma quali sono le funzioni che possiamo trovarci davanti?
Qualche esempio lo abbiamo già visto. Che cosa sono le equazioni del tipo £$ y = f(x) $£?
Le funzioni sono espresse da una formula che contiene le due variabili £$ x $£ e £$ y $£, una legge matematica che lega queste due variabili.
Esempio: £$ y = x + 1 $£ è una funzione che associa ad un numero £$ x $£ il suo successivo £$ x + 1 $£. Consideriamo come insieme di partenza £$ X $£ l’insieme dei numeri naturali £$ \mathbb{N} $£. Ovviamente l’insieme di arrivo £$ Y $£ è ancora uguale all’insieme dei numeri naturali £$ \mathbb{N} $£. Costruiamo la tabella in cui visualizzare i valori che la funzione mette in relazione:
| £$\ x \ $£ | £$ \ y \ $£ |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
Esempio: Possiamo rappresentare così la funzione che associa alla misura del lato di un quadrato la sua area: £$ y = x^2 $£. Rappresentiamo i valori che assume la funzione con una tabella:
| £$\ x \ $£ | £$\ y \ $£ |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
In verità abbiamo già visto delle funzioni. Ti ricordi le grandezze direttamente e inversamente proporzionali? Le abbiamo rappresentate attraverso delle funzioni (retta e iperbole), con variabile dipendente e variabile indipendente e disegnando il grafico sul piano cartesiano.
I metodi per rappresentare graficamente una funzione
Rappresentazione insiemistica
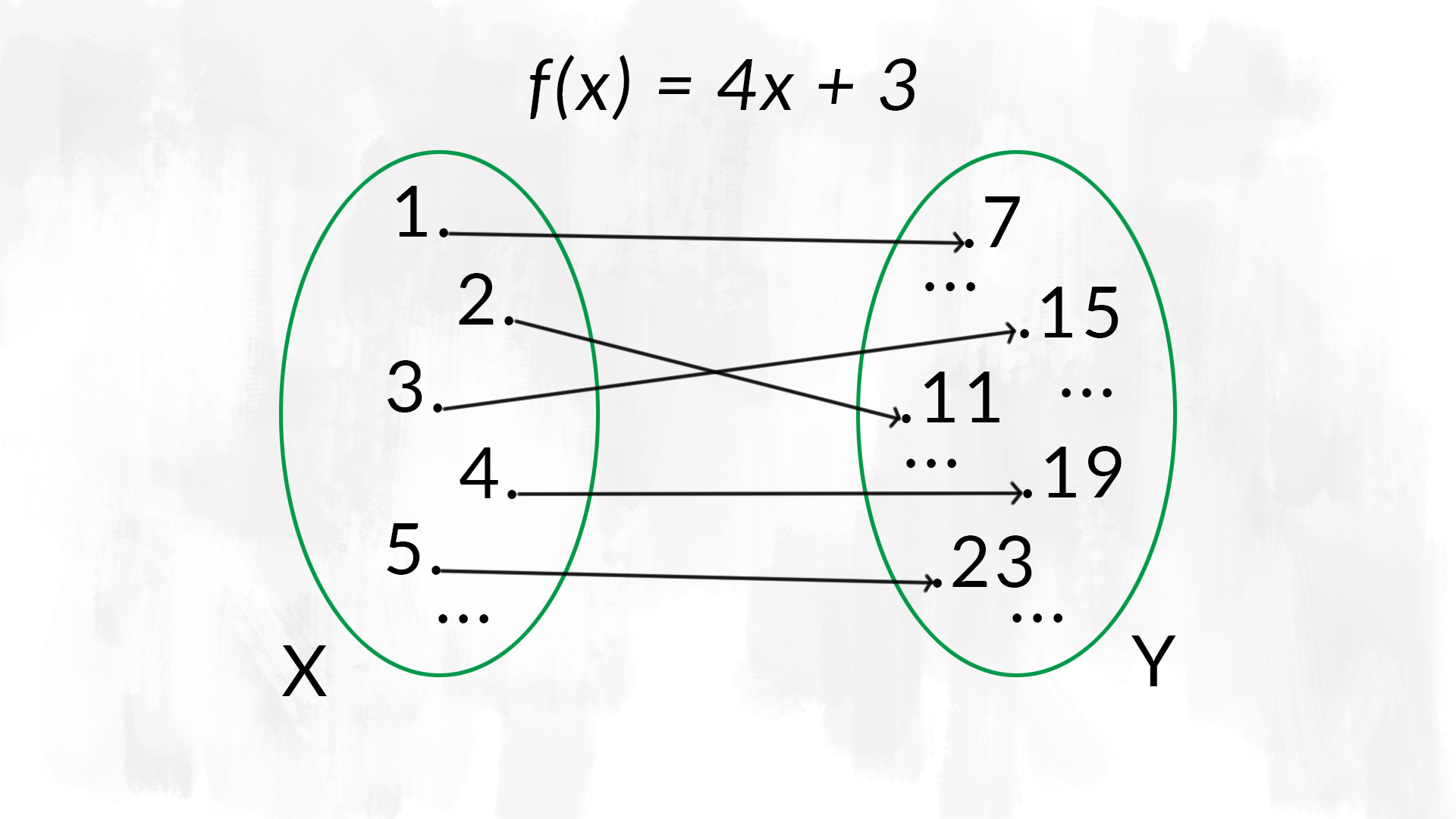
Grafico della funzione

Abbiamo detto che una funzione è una particolare relazione tra due insiemi. Il primo modo per rappresentarla è proprio quello insiemistico.
Una funzione tra due insiemi può essere rappresentata con delle frecce che collegano ciascun elemento dell’insieme di partenza con un unico elemento dell’insieme di arrivo.
Un altro modo per rappresentare una funzione è disegnango il suo grafico sul piano cartesiano. La funzione mette in relazione un elemento £$ x \in X $£ con un elemento £$ y \in Y $£. Gli elementi messi così in relazione formano delle coppie £$ (x;y) $£. Ciascuna di queste coppie indica le coordinate di un punto sul piano cartesiano. Quindi possiamo rappresentare il grafico di una funzione unendo tutti i punti sul piano cartesiano: a partire dalla legge matematica che definisce la funzione, riusciamo a ricavare tutte le coordinate. Stabiliamo una £$ x $£ e troviamo il valore della variabile dipendente £$ y $£. Individuati tutti i punti, ecco il grafico della funzione!
Esempio: nelle due immagini abbiamo rappresentato nei due modi diversi la stessa funzione, definita da £$ \mathbb{N} $£ in £$ \mathbb{N} $£:
£$ f(x) = 4x + 3 $£
Come riconoscere una funzione
Funzioni
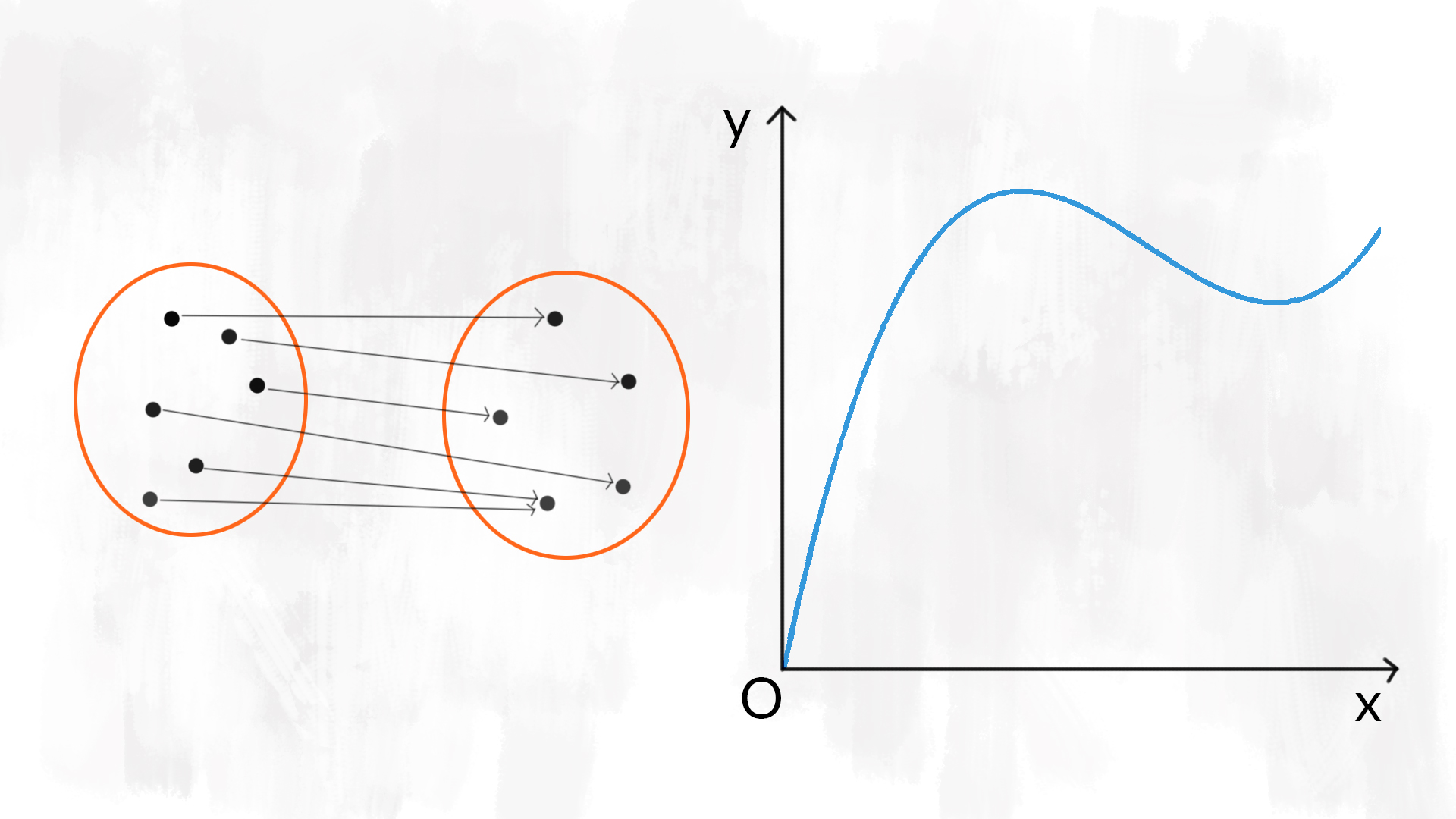
Relazioni che non sono funzioni

Non tutte le relazioni tra due insiemi sono delle funzioni. Bisogna imparare a riconoscerle! Il passaggio più importante per riconoscere una funzione è controllare che tutti gli elementi nell’insieme di partenza abbiano un unico corrispondente nell’insieme di arrivo. Quindi fai attenzione che non ci sia un elemento £$ x \in X $£ tale che £$ f(x) = y_1 $£ e £$ f(x) = y_2 $£ con £$ y_1 \ne y_2 $£.
Nella rappresentazione insiemistica riconosciamo che la relazione rappresentata è una funzione se da ciascun elemento dell’insieme di partenza £$ X $£ “esce un’unica freccia" che lo collega ad un unico elemento dell’insieme £$ Y $£.
Nella rappresentazione sul piano cartesiano, invece, possiamo utilizzare il metodo delle linee verticali: immaginiamo di tracciare delle linee verticali (cioè parallele all’asse £$ y $£) sul piano cartesiano. Se anche solo una di queste linee interseca il grafico in due punti, allora quello che abbiamo davanti non è il grafico di una funzione.
