I connettivi logici in matematica: cosa sono e a cosa servono
La matematica non è fatta solo di numeri e segni: molti elementi possono essere compresi soltanto attraverso la logica. Alcuni dei capisaldi della logica ci permettono di esprimere e collegare proposizioni: questi strumenti sono conosciuti come “connettivi logici“. Se la matematica fosse paragonata al linguaggio, i connettivi logici sarebbero gli equivalenti di congiunzioni come “e", “o", “non" e “ma".
Ma cosa sono esattamente i connettivi logici e qual è la loro funzione all’interno della matematica? Queste sono le risposte alle quali cercheremo di dare una risposta nel nostro articolo di oggi!
I connettivi logici sono operatori che combinano proposizioni singole per formare proposizioni composte. Ad esempio, prendendo due semplici affermazioni, “Piove" e “Ho l’ombrello", possiamo usarle insieme con un connettivo logico per formare “Piove E ho l’ombrello", esprimendo un concetto combinato. Queste combinazioni possono essere utilizzate per rappresentare, analizzare e ragionare su situazioni complesse, creando una struttura di pensiero razionale e sequenziale.
In matematica, i connettivi logici più comuni sono: “E" (congiunzione), “O" (disgiunzione), “SE… ALLORA…" (implicazione), “NON" (negazione). Ciascuno di questi ha un ruolo specifico e una definizione precisa che impareremo insieme.
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Le proposizioni composte in matematica
- Il connettivo logico più elementare: la negazione
- Come creare proposizioni composte con i connettivi logici
- I connettivi logici in matematica: la congiunzione, la disgiunzione e l'implicazione
- Connettivi logici e operazioni tra gli insiemi
Le proposizioni composte in matematica
Così come le parole possono essere composte per formare frasi, anche nel linguaggio della logica le proposizioni semplici possono essere composte per formare proposizioni più complesse per esprimere pensieri più elaborati.
La proposizione logica composta è una frase formata da più proposizioni logiche semplici che, in quanto proposizione, può essere o vera o falsa.
Ad esempio, prendiamo due proposizioni semplici:
- £$A$£: “il mio gelato è al cioccolato"
- £$B$£: “il mio gelato ha la panna"
Possiamo legarle tra loro nella proposizione composta:
£$C$£: “il mio gelato è al cioccolato ed ha la panna"
Le proposizioni composte sono formate da più predicati (cioè da più proposizioni semplici):
“Il mio gatto è bianco ed ha le macchie" è una proposizione composta formata da due predicati “è" e “ha" e dalle due proposizioni semplici “il mio gatto è bianco" e “il mio gatto ha le macchie".
Altri esempi di proposizioni composte sono:
- Le carte sono di seme rosso o sono di seme nero
- La lampadina rossa o è accesa o è spenta.
Anche le proposizioni logiche composte sono vere o false. Il loro valore di verità dipende da quello delle proposizioni semplici che le compongono.
Il connettivo logico più elementare: la negazione
Cominciamo con l’operatore più semplice, la negazione, che opera a partire da una singola proposizione.
La negazione è un operatore logico unario (cioè agisce su una sola proposizione) che rende falsa una frase vera e rende vera una frase falsa. Si esprime tramite la particella ‘non’.
Data la proposizione £$A$£, la sua negazione viene indicata con £$\overline{A}$£ (si legge “non £$A$£" oppure “£$A$£ barrato").
Data la proposizione semplice
- £$A$£: “La lampadina è accesa" { £$A$£ è vera }
La sua negata è:
- £$\overline{A}$£: “La lampadina non è accesa’’ { £$\overline{A}$£ è falsa }
Se £$A$£ è vera, allora £$\overline{A}$£ è falsa… e viceversa:
- £$A$£: “La lampadina non è accesa" { £$A$£ è falsa }
La sua negata è:
- £$\overline{A}$£: “La lampadina è accesa’’ { £$\overline{A}$£ è vera }
Un altro esempio è dato dalla proposizione:
- £$p$£: “Questo è un asso di picche" { £$p$£ è Falsa}
La sua negata è:
- £$\overline{p}$£: “Questo non è un asso di picche’’ {£$\overline{p}$£ è Vera}
Dunque il valore di verità di £$\overline{p}$£ dipende dal valore di verità di £$p$£, ed è il suo opposto.
La negazione scambia i valori di verità: ciò che è vero diventa falso e ciò che è falso diventa vero.
Posso applicare la negazione tutte le volte che voglio. Ad esempio:
£$A$£: “La lampadina è accesa."
£$\overline{A}$£ : “La lampadina non è accesa."
£$\overline{( \overline{A})}$£: “Non è che la lampadina non è accesa."
£$\overline{( \overline{(\overline{A})})}$£: “Non è che non è che la lampadina non è accesa."
Grazie alla tavola di verità conosco il valore di verità delle proposizioni composte. Dalle tavole di verità si può inoltre dedurre che due negazioni confermano il valore di verità.
Attenzione! La negazione della frase “tutti i gatti sono neri" è:
“Non è vero che tutti i gatti sono neri", oppure “Non tutti i gatti sono neri."
NON è: “Nessun gatto è nero"
Come creare proposizioni composte con i connettivi logici
Come comporre due proposizioni semplici? Ci sono diversi modi, vediamone alcuni.
Date due proposizioni semplici
- £$A$£: “Il mio gatto è bianco."
- £$B$£: “Il mio gatto porta la corona."
Posso comporle e formare molte proposizioni composte, ad esempio
- Il mio gatto è bianco e porta la corona.
- Il mio gatto non è bianco e non porta la corona.
- Se il mio gatto non è bianco allora non porta la corona.
- Il mio gatto o è bianco o porta la corona.
Le particelle ‘e’, ‘o’, ‘non’, ‘se…allora’ sono chiamati operatori logici e servono per formare proposizioni composte.
Le proposizioni composte possono essere formate utilizzando molti operatori logici e possono avere molti predicati.
I connettivi logici in matematica: la congiunzione, la disgiunzione e l’implicazione
I connettivi logici in matematica sono molto simili a quelli che incontriamo anche in italiano, ma hanno una funzione diversa a seconda del contesto nel quale li troviamo e possono tornarci particolarmente utili quando abbiamo a che fare con gli insiemi numerici. Vediamo insieme quali sono le tipologie di connettivi più diffuse e utilizzate.
La congiunzione
Formiamo una proposizione composta a partire da queste due proposizioni semplici usando il connettivo “e".
£$p$£: “Un quadrato è un rettangolo" (VERA)
£$q$£: “Un quadrato è un rombo’’ (VERA)
La proposizione composta “Un quadrato è un rettangolo ed è un rombo’’ è VERA. Il connettivo “e" si chiama congiunzione e la proposizione così composta si rappresenta con il simbolo £$p\wedge q$£.
Cosa succede quando le proposizioni sono false? Rappresentiamo la congiunzione con la sua tavola di verità.
$$\begin{array}{|c|c|c|} \hline p&q&p\wedge q\\\hline V&V&V\\\hline V&F&F\\\hline F&V&F\\\hline F&F&F\\\hline \end{array}$$
La congiunzione è vera soltanto quando le proposizioni che la compongono sono entrambe vere. In tutti gli altri casi è falsa!
Per esempio:
£$p$£: “£$8$£ è un multiplo di £$2$£" (VERA)
£$q$£: “£$8$£ è un multiplo di £$3$£’’ (FALSA)
La proposizione composta “£$8$£ è un multiplo di £$2$£ ed è un multiplo di £$3$£’’ è FALSA.
La disgiunzione
Un altro connettivo logico è “o", che si chiama disgiunzione.
Consideriamo le due proposizioni:
£$p$£: “£$9$£ è dispari" (VERA)
£$q$£: “£$9$£ è primo" (FALSA)
La proposizione composta con la disgiunzione “o" è “£$9$£ è dispari o £$9$£ è primo’’ e si indica con il simbolo £$p \vee q$£. Questa proposizione è VERA! Infatti una proposizione composta con la disgiunzione è vera se almeno una delle due proposizioni semplici lo è.
Rappresentiamo la disgiunzione con la sua tavola di verità.
$$\begin{array}{|c|c|c|} \hline p&q&p\vee q\\\hline V&V&V\\\hline V&F&V\\\hline F&V&V\\\hline F&F&F\\\hline \end{array}$$
La disgiunzione è falsa soltanto quando le proposizioni che la compongono sono entrambe false. In tutti gli altri casi è vera!
Per esempio:
£$p$£: “Un triangolo equilatero ha un angolo retto" (FALSA)
£$q$£: “Un quadrato ha un angolo acuto ’’ (FALSA)
La proposizione composta “Un triangolo equilatero ha un angolo retto o un quadrato ha una angolo acuto’’ è FALSA.
Fai attenzione! Nel linguaggio di tutti i giorni utilizziamo la disgiunzione “o" in due modi diversi:
“Prima di andare a dormire bevo una camomilla o guardo la televisione". Questa frase è vera anche se bevo la camomilla guardando la televisione. Questa è la disgiunzione che abbiamo già visto! Si chiama anche disgiunzione inclusiva.
“Stamattina metto una maglia blu o una maglia rossa". In questo caso non può accadere contemporaneamente di indossare una maglia blu e una maglia rossa. Questa disgiunzione si chiama esclusiva.
L’implicazione
Un altro modo per collegare due proposizioni semplici è l’implicazione. È una proposizione composta che collega due proposizioni semplici attraverso l’espressione “se… allora".
Possiamo indicare questa proposizione utilizzando il simbolo £$ \rightarrow $£ oppure anche il simbolo £$ \Rightarrow $£.
Consideriamo due proposizioni semplici £$ p $£ e £$ q $£. Possiamo leggere l’espressione £$ p \rightarrow q $£ come “£$p$£ implica £$q$£" oppure come “se £$p$£ allora £$q$£“. La prima proposizione, £$ p $£, è la premessa, la seconda proposizione, £$ q $£, è la conclusione.
Come facciamo a capire se una implicazione è vera o è falsa? Se la conclusione è vera tutte le volte che è vera la premessa, anche l’implicazione è vera.
Per esempio:
- l’implicazione £$ p \rightarrow q $£: “Se £$ n $£ è un numero primo allora è divisibile per 2" è FALSA. Infatti la conclusione £$ q $£: “£$ n $£ è divisibile per 2" è FALSA, se assumiamo che la premessa £$ p $£: “£$ n $£ è un numero primo" è VERA;
- l’implicazione £$ p \rightarrow q $£: “Se £$ n $£ è un numero primo allora è divisibile per 1 e per se stesso" è VERA. Infatti la conclusione £$ q $£: “£$ n $£ è divisibile per 1 e per se stesso" è VERA e anche la premessa £$ p $£: “£$ n $£ è un numero primo" è VERA.
Proviamo a capirlo meglio con la tavola di verità dell’implicazione:
$$\begin{array}{|c|c|c|} \hline p&q&p\rightarrow q\\\hline V&V&V\\\hline V&F&F\\\hline \end{array}$$
Connettivi logici e operazioni tra gli insiemi
Congiunzione e intersezione
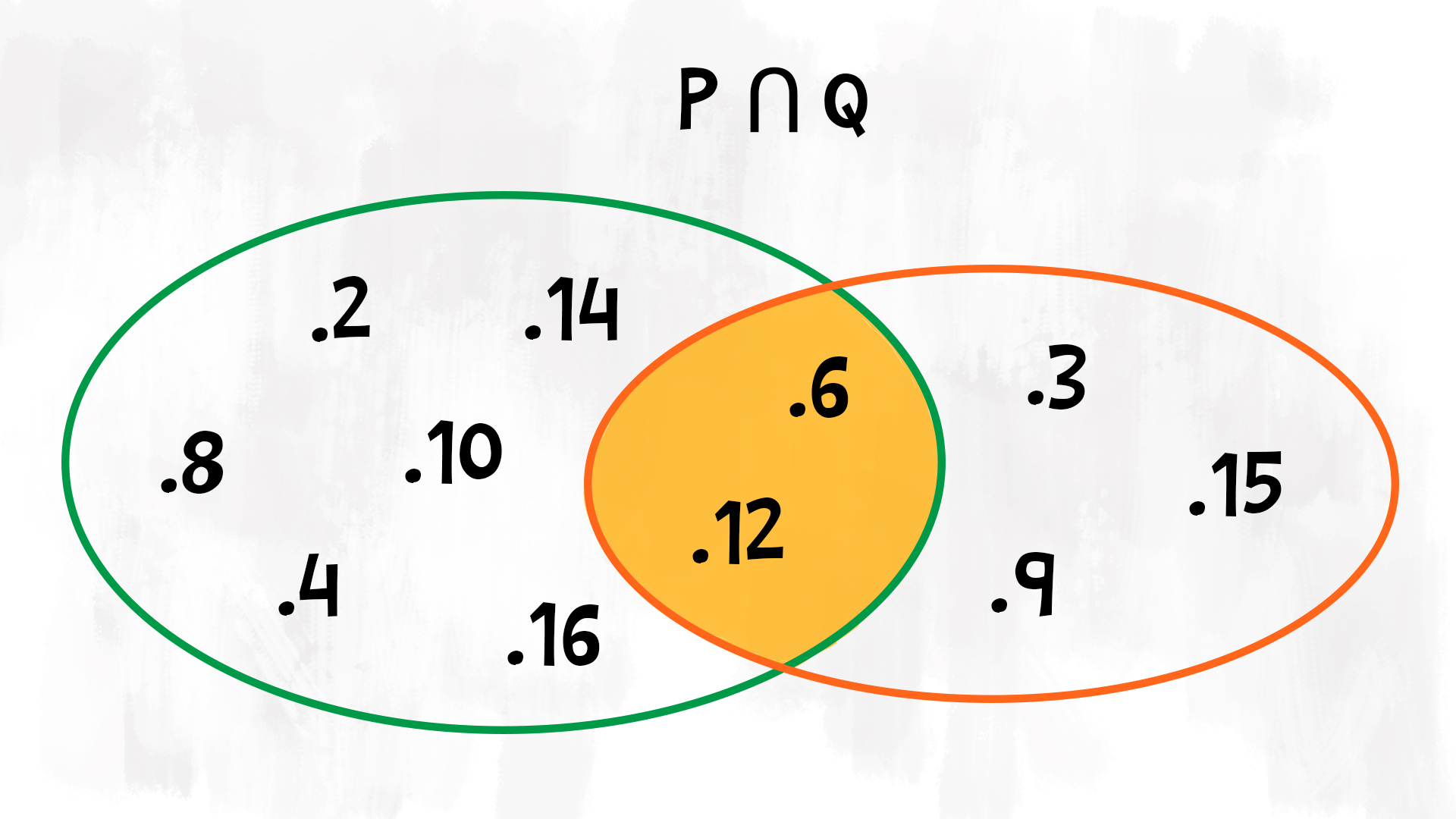
I connettivi logici di congiunzione e disgiunzione funzionano un po’ come le operazioni tra gli insiemi.
La congiunzione corrisponde all’intersezione. Infatti una congiunzione è vera solo se le due proposizioni che la compongono sono entrambe vere. Nello stesso modo, diciamo che degli elementi appartengono all’intersezione di due insiemi solo se appartengono sia al primo che al secondo insieme.
Esempio: £$ P \cap Q = \{6, 12 \} $£ perché £$ 6, 12 \in P \wedge 6, 12 \in Q $£.
La disgiunzione funziona come l’unione. Infatti perché una disgiunzione sia vera è sufficiente che almeno una delle proposizioni che la compongono sia vera. Nello stesso modo, diciamo che degli elementi appartengono all’unione di due insiemi se appartengono ad almeno uno dei due insiemi.
Esempio: £$ P \cup Q = \{2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16 \} $£ perché sono tutti gli elementi che appartengono all’insieme £$ P $£ o all’insieme £$ Q $£.
Disgiunzione e unione
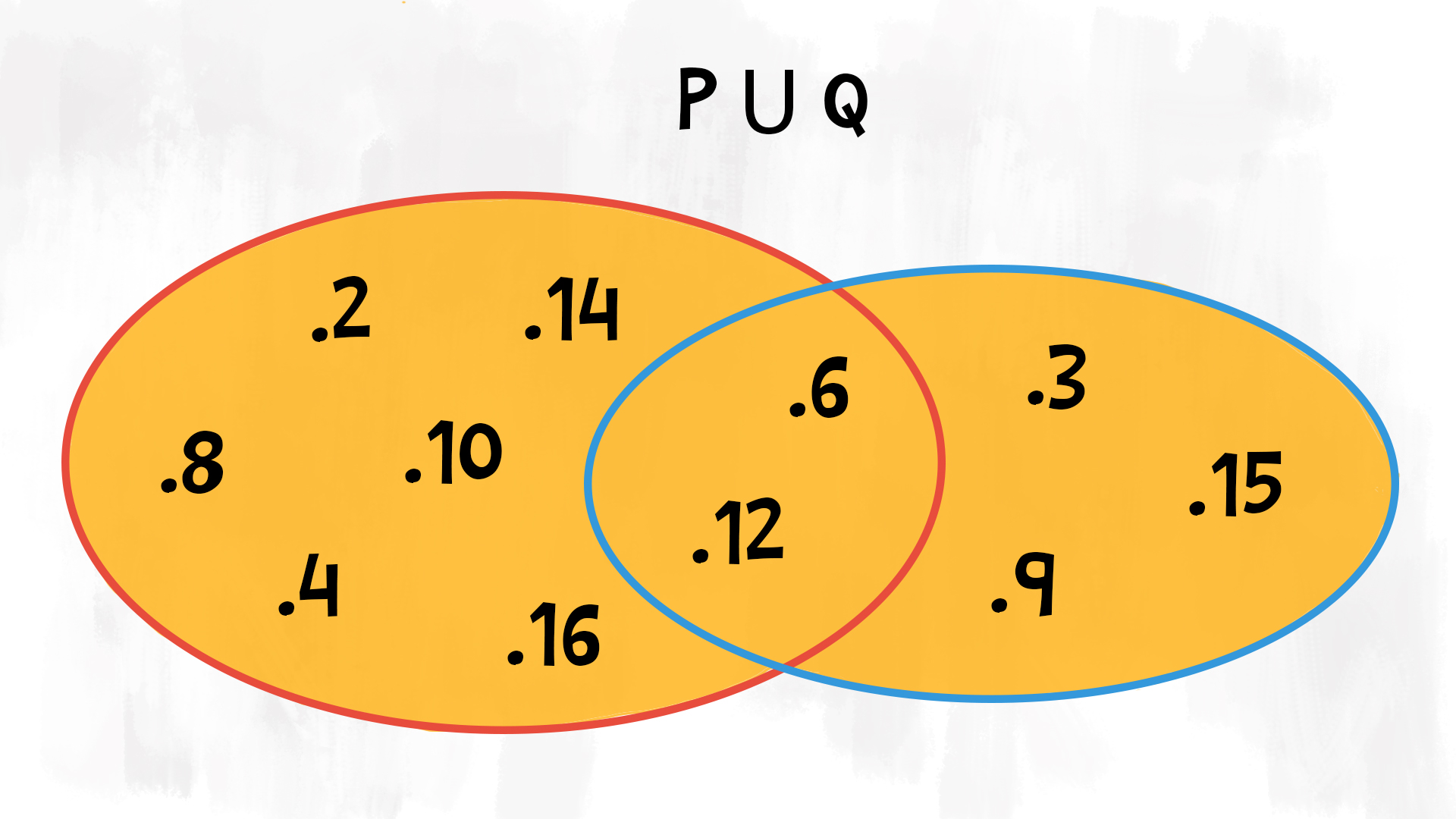
La disgiunzione funziona come l’unione. Infatti perché una disgiunzione sia vera è sufficiente che almeno una delle proposizioni che la compongono sia vera. Nello stesso modo, diciamo che degli elementi appartengono all’unione di due insiemi se appartengono ad almeno uno dei due insiemi.
Esempio: £$ P \cup Q = \{2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16 \} $£ perché sono tutti gli elementi che appartengono all’insieme £$ P $£ o all’insieme £$ Q $£.
