Moto circolare uniforme: definizione e formule
Il moto circolare uniforme è un moto nel quale un corpo si muove in rotazione mantenendo una traiettoria circolare e costante. In questa lezione affronteremo tutte le formule legate a questa tipologia di moto e affronteremo tutte le definizioni del caso!
Vuoi testare la tua preparazione? Prova il nostro quiz!
- Vettori del moto circolare uniforme
- Periodo e frequenza del moto circolare uniforme
- L'accelerazione del moto circolare uniforme
- Dimostrazione dell'accelerazione centripeta
- La velocità angolare nel moto circolare uniforme
Vettori del moto circolare uniforme
La punta della lancetta di un orologio si muove con la stessa velocità, e se potessimo unire tutti i punti da cui essa passa troveremmo una circonferenza. La punta della lancetta di un orologio, se si muove senza mai fermarsi, viaggia con un moto circolare uniforme.
Il moto circolare uniforme è un moto in cui il punto materiale viaggia con la stessa velocità istantanea tangenziale su una traiettoria circolare. Il modulo del vettore velocità istantanea resta costante.
Si dice tangenziale perché nel moto circolare uniforme il vettore velocità ha direzione tangente alla circonferenza e lo stesso verso dello spostamento, che segue il senso del moto (orario o antiorario).
Un punto materiale che si muove di moto circolare uniforme percorre archi di circonferenza direttamente proporzionali agli intervalli di tempo impiegati.
Periodo e frequenza del moto circolare uniforme
II periodo ( £$T$£ ) è il tempo impiegato dal punto materiale per compiere un giro completo e viene misurato in secondi (£$\text{s}$£).
Il numero di giri che il punto compie in un secondo, invece, si chiama frequenza ( £$f$£ ) e si misura in Hertz (£$\text{Hz}$£).
£$1 \ \text{Hz}$£ equivale a £$\frac{1}{\text{s}}$£, quindi la frequenza equivale a £$\frac{1}{T}$£.
La velocità tangenziale, nel moto circolare uniforme, ha modulo uguale al rapporto tra lo spazio percorso e il tempo compiuto (dato che essa rimane costante) quindi possiamo calcolare il modulo della velocità dividendo la lunghezza della circonferenza per il periodo.
£$v$£ = £$\frac{C}{T}$£ = £$\frac{2\pi \ r}{T}$£
L’accelerazione del moto circolare uniforme
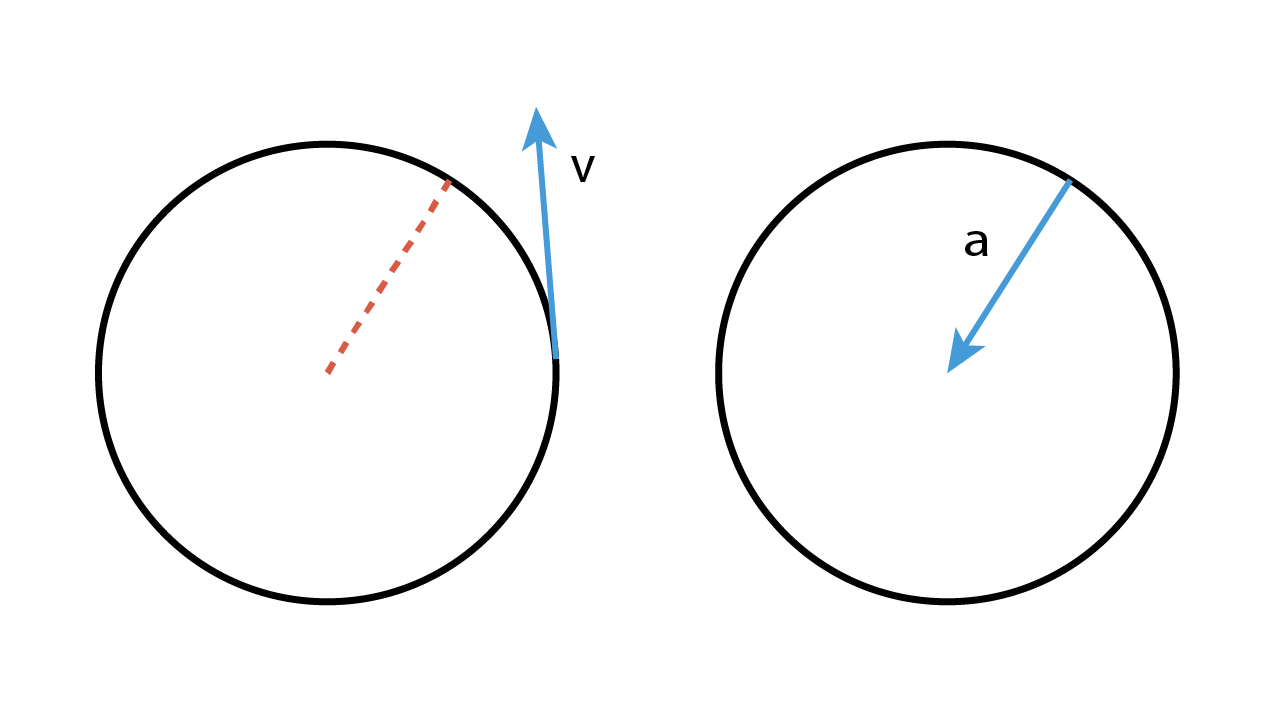
L’accelerazione è data dal rapporto tra la variazione della velocità e la variazione del tempo.
Anche se la velocità è costante, in ogni punto del moto l’accelerazione totale del moto circolare uniforme è diversa da 0. Questo perché l’unico elemento costante nei vettori velocità è il modulo! Gli altri due elementi (direzione e verso) non sono costanti, ma variano in ogni punto della circonferenza.
L’accelerazione è quindi il rapporto tra £$\Delta{v}$£ e £$\Delta{t}$£.
Il vettore variazione di velocità £$\Delta{v}$£, se consideriamo un piccolo intervallo di tempo £$\Delta{t}$£, è un vettore che ha come direzione una retta passante per il centro e verso rivolto verso il centro, per questo viene chiamata accelerazione centripeta (dal latino centrum = centro; petere = dirigersi).
Questo vettore avrà come modulo il rapporto tra il quadrato della velocità tangenziale e il raggio. £$a_c$£ = £$\frac{v^2}{r}$£
In altri moti circolari potrebbe essere presente anche un’accelerazione tangenziale (con direzione tangente alla circonferenza), nel moto rettilineo uniforme essa è uguale a 0.
Dimostrazione dell’accelerazione centripeta
Due vettori velocità (£$v_A$£ e £$v_B$£) agiscono in due punti diversi della circonferenza, molto vicini tra loro (£$A$£ e £$B$£), uniamo le loro code nel punto £$A$£. Osserviamo che si forma un triangolo isoscele formato dai due vettori e dal vettore variazione di velocità £$\Delta{v}$£, dato che i due vettori velocità hanno lo stesso modulo. Tra i due vettori velocità è compreso un angolo £$\theta$£.
Osserviamo ora il triangolo formato da due raggi £$OA$£ e £$OB$£ e dal vettore spostamento che unisce i punti £$A$£ e £$B$£ (£$\Delta{s}$£). Anche questo triangolo è isoscele poiché i due raggi sono uguali. L’angolo compreso tra i due raggi è, invece, congruente all’angolo £$\theta$£, dato che i due raggi £$OA$£ e £$OB$£ sono rispettivamente perpendicolari ai vettori £$v_A$£ e £$v_B$£, e l’angolo compreso tra due semirette è congruente all’angolo compreso tra due semirette perpendicolari a quelle date.
Quindi per il secondo criterio di similitudine i due triangoli sono simili, e quindi vale la proporzione £$\dfrac{r}{v} = \dfrac{\Delta{s}}{\Delta{v}}$£.
In questo caso i due punti £$A$£ e £$B$£ sono molto vicini, quindi possiamo approssimare l’arco £$AB$£ ad un segmento £$AB$£ congruente a £$\Delta{s}$£.
Quest’ultimo è dato dal prodotto £$v \ \cdot \ t$£, visto che la velocità tangenziale è costante.
Ora la proporzione si può scrivere cosi: £$\dfrac{r}{v} = \dfrac{v \ \cdot \ t}{\Delta{v}}$£
Quindi £$\Delta{v}$£ = £$\dfrac{v^2 \ \cdot \ t}{r}$£
Ma £$a_c$£ = £$\dfrac{\Delta{v}}{\Delta{t}}$£; quindi £$a_c$£ = £$\dfrac{v^2}{r}$£
La velocità angolare nel moto circolare uniforme
Nel moto circolare uniforme la velocità tangenziale varia a seconda della distanza dal centro (raggio).
Esempio.
Se una mosca dovesse trovarsi aggrappata alla punta di un elica di un elicottero andrà sicuramente più veloce di un’altra che si trova aggrappata a pochi centimetri dall’albero rotante.
Infatti abbiamo visto che £$v$£ = £$\frac{2\pi \ \cdot \ r}{T}$£; quindi la velocità tangenziale (o istantanea) è direttamente proporzionale al raggio.
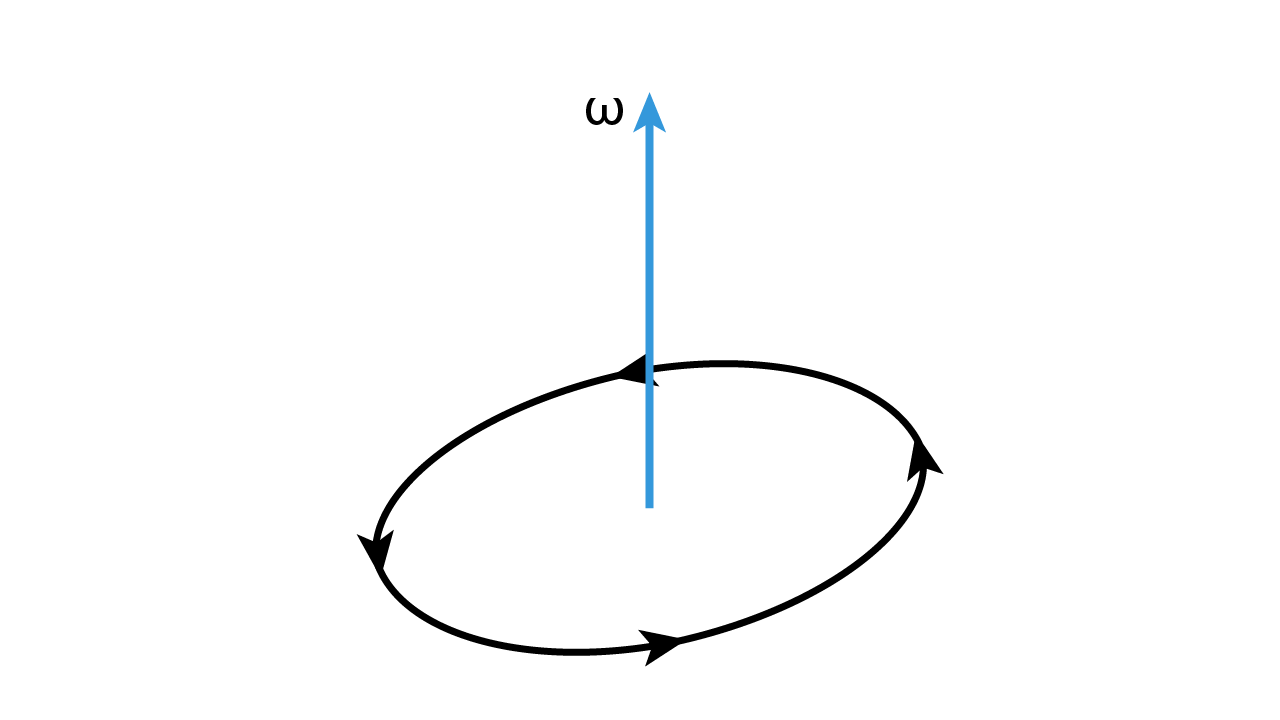
Ciò che non varia a seconda del raggio è invece la velocità angolare (£$\omega$£), definita come la variazione di un angolo nel tempo.
Questa grandezza è una grandezza vettoriale che ha come direzione l’asse di rotazione (perpendicolare al piano di rotazione), verso uscente dal piano se il giro è antiorario (entrante se viceversa) e modulo equivalente al rapporto tra l’angolo spazzato dal raggio in un intervallo di tempo in radianti e il tempo stesso.
La velocità angolare si misura in £$\frac{rad}{s}$£.
£$\omega$£ = £$\frac{\theta}{t}$£
Se non ricordi gli angoli in radianti, clicca qui!
La velocità angolare si può anche ricavare dal rapporto £$\frac{velocità \ tangenziale}{raggio}$£ → £$\omega$£ = £$\frac{v}{r}$£;
£$\omega$£ è infatti la costante di proporzionalità del rapporto £$\frac{v}{r}$£.
Esempio.
In un tempo equivalente al periodo il raggio spazza un angolo giro:
(£$360°= 2\pi$£), quindi basta conoscere il periodo per trovare la velocità angolare di un moto circolare uniforme: £$\omega$£ = £$\frac{2\pi}{T}$£
£$a_c$£ = £$\frac{v^2}{r}$£ quindi £$a_c$£ = £$\frac{\omega^{2}r^2}{r}$£ = £$\omega^{2}r$£
