Moto rettilineo uniforme: formule e definizione
Il moto rettilineo uniforme si caratterizza dal fatto che la velocità sia costante nel tempo: si tratta di un corpo che si muove secondo un moto rettilineo, quindi un percorso in linea retta, uniforme. Ciò significa che percorre spazi uguali in tempi uguali.
Il grafico di questo moto, rappresentato sul piano cartesiano, è infatti una retta. Ma scopriamo tutti gli elementi più nel dettaglio: in questo articolo studieremo la definizione del moto rettilineo uniforme, impareremo che cos’è e quali sono le formule che lo caratterizzano insieme ai nostri esempi.
- La legge oraria del moto rettilineo uniforme
- Grafico spazio-tempo del moto rettilineo uniforme
- Grafico velocità-tempo del moto rettilineo uniforme
- La nuotata rettilinea della balenottera
La legge oraria del moto rettilineo uniforme

Il moto rettilineo uniforme è un moto con:
- la traiettoria rappresentata da una linea retta;
- Il rapporto £$\frac{spazio}{tempo}$£ costante, quindi la velocità è costante.
La legge oraria è l’equazione che caratterizza l’andamento della posizione in funzione del tempo.
Quindi la legge oraria del moto rettilineo uniforme è £$\Delta{S}$£ = £$v \ \cdot \ \Delta{t}$£ che si può scrivere anche come £$\frac{\Delta{S}}{\Delta{t}}$£ = £$v$£
Nel moto rettilineo uniforme le distanze sono direttamente proporzionali agli intervalli di tempo impiegati a percorrerle.
Attenzione!
£$\Delta{S}$£ significa che solo lo spostamento che il punto materiale compie quando si muove di moto rettilineo uniforme è uguale al prodotto £$v \ \cdot \ \Delta{t}$£, con £$\Delta{S}= S – S_i$£
Con £$S$£ = posizione finale
Con £$S_i$£ = posizione iniziale
Grafico spazio-tempo del moto rettilineo uniforme
£$S_i = 0$£

£$S_i \neq 0$£
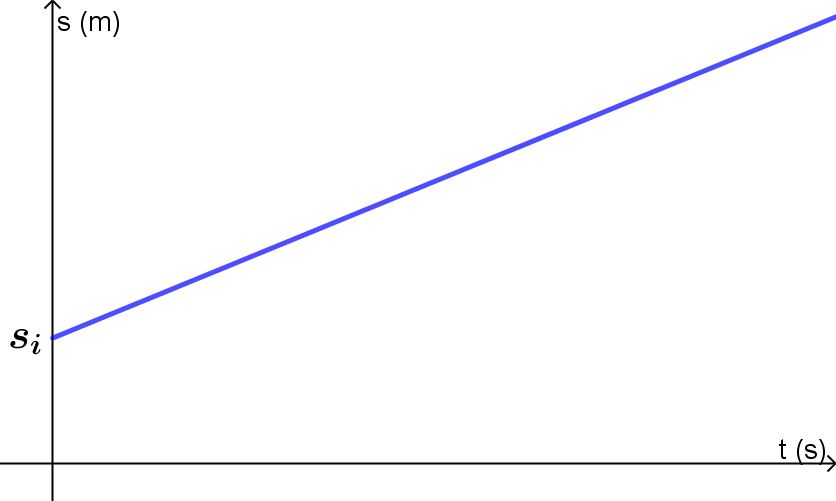
Se rappresentiamo il moto rettilineo uniforme su un grafico cartesiano spazio-tempo il risultato sarà una linea retta, visto che £$\Delta{s}$£ e £$\Delta{t}$£ sono direttamente proporzionali, essendo il loro rapporto, ovvero la velocità, costante in ogni punto.
Questa retta passa per l’origine se £$S_i$£ = 0.
Se, invece, £$S_i$£ ≠ 0, allora questa retta intersecherà l’asse delle y nel punto (0;£$S_i$£).
La retta avrà equazione: £$S$£ = £$v \ \cdot \ \Delta{t}$£ + £$S_i$£ quindi la velocità del punto materiale sarà il coefficiente angolare.
Più la retta è inclinata verso l’asse y, più il punto materiale andrà veloce (se si usa la stessa unità per le ascisse e per le ordinate).
Grafico velocità-tempo del moto rettilineo uniforme
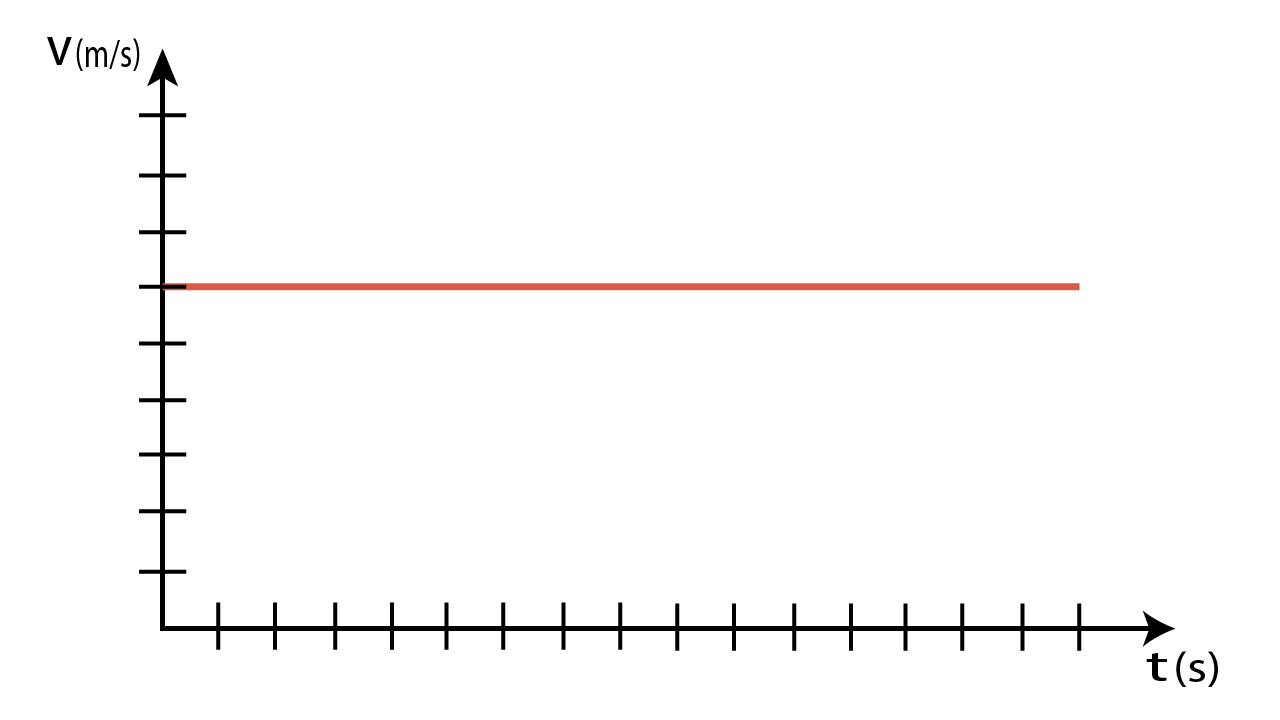
Se rappresentiamo il moto su un grafico cartesiano sostituendo le ordinate con la velocità (grafico cartesiano velocità-tempo) troviamo una retta parallela all’asse x.
Perché?
La velocità è costante ed è rappresentata da una retta di equazione y = £$v$£
Lo spazio è rappresentato dal prodotto £$v \ \cdot \ \Delta{t}$£, quindi questo grafico può essere ricavato calcolando l’area del rettangolo sottostante la funzione, compreso tra due intervalli di tempo.
In generale lo spazio può essere ricavato nel grafico velocità-tempo calcolando l’area sottostante la funzione.
La nuotata rettilinea della balenottera

Una tranquilla nuotata rettilinea della balenottera, con regolari colpi di pinna.
Due banchi di krill galleggiano tranquilli sulla superficie dell’Atlantico Settentrionale, non lontano dalla costa dell’Islanda. La nostra balenottera azzurra, dopo averci aiutato nella scoperta di scalari e vettori, procede in linea retta alla ricerca di cibo, mantenendo costante la propria velocità £$v$£ con colpi di pinna regolari.
Se indichiamo con £$x$£ la direzione lungo la quale la balenottera procede, e con £$x_1$£ e £$x_2$£ la posizione nella quale si trovano i due banchi di krill, possiamo affermare che la balenottera raggiunge il primo banco di krill al tempo £$t_1$£ e il secondo banco di krill al tempo £$t_2$£, percorrendo uno spazio £$\Delta{x}$£ in un tempo £$\Delta{t}$£.
Generalizzando, possiamo affermare che lo spazio percorso dalla balenottera alla ricerca di cibo sia £$x = x(t)$£, ossia lo spazio percorso è esclusivamente in funzione del tempo impiegato a percorrerlo. La funzione £$x(t)$£ mette in relazione lo spazio percorso £$x$£ (espresso in metri) con il tempo £$t$£ (espresso in secondi) in cui quello spazio viene percorso.
La funzione £$x = x(t)$£ è definita legge oraria del moto.
Spazio e tempo nel moto rettilineo della balenottera sono messi in funzione dalla velocità del cetaceo: £$v = \dfrac{(x_2 – x_1)}{(t_2 – t_1)}$£.
La balenottera, che ci ha visto tracciare l’espressione appena descritta, insorge: salta fuori dall’acqua e ci fa notare che l’espressione, che pure è corretta nel caso specifico, può essere scritta in modo più completo e generale in forma vettoriale: £$v = \dfrac{\Delta{x}}{\Delta{t}}$£, incorporando quindi la direzione e il verso del moto rettilineo della balenottera.
Il moto di una balenottera.
Tenendo conto del moto della balenottera istante per istante, e selezionando un istante iniziale £$t_0$£ e una posizione iniziale £$x_0$£ nella nostra valutazione del fenomeno, possiamo scrivere la legge oraria come segue:
£$x(t)$£= £$x(t_0)$£ + £$x(t-t_0)$£
che ci dice che, al tempo £$t$£, la posizione £$x$£ della balenottera è data dalla sua posizione all’istante iniziale £$t_0$£ più lo spazio percorso dalla sua posizione iniziale £$x_0$£ nell’istante £$t_0$£ fino al tempo £$t$£ in ragione della sua velocità £$v$£. Potremo quindi, armati di metro e cronometro (o meglio, armati di sonar, che ci indica le posizioni mantenendoci a una distanza sicura, e di cronometro), misurare le coppie (£$x_i,t_i$£), con £$i=1$£,… e ottenere la posizione della balenottera in ogni istante per l’intero fenomeno della predazione, fino al momento e alla posizione finali, £$t$£ e £$x$£.
È ora semplice mettere in un piano cartesiano il percorso rettilineo della balenottera:
- in ascissa indicheremo i tempi, da £$t_0$£ a £$t$£,
- in ordinata le posizioni, da £$x_0$£ a £$x$£
Otteniamo, come ci aspettavamo, una linea retta il cui coefficiente angolare è la velocità costante che la balenottera ha voluto tenere £$v$£.
Il Moto Rettilineo Uniforme di una balenottera.
La balenottera ci ha aiutato a verificare la relazione lineare esistente tra spazio percorso e tempo impiegato a percorrerlo: se questo spazio è percorso a velocità costante e lungo una linea retta, il moto si definisce rettilineo uniforme ed è descritto da una legge oraria lineare.
Per descrivere compiutamente il moto rettilineo uniforme, è sufficiente conoscere due tra le tre grandezze (velocità, tempo, spazio) e ricavare la terza; nel momento in cui osserviamo il fenomeno del pranzo della balenottera, abbiamo la possibilità di misurare due tra le tre grandezze e ricavare la terza.
La messa in grafico dei dati ci permette una prima verifica della correttezza della nostra misurazione: se il risultato è una retta abbiamo fiducia di aver misurato un moto rettilineo uniforme, la cui velocità ci è data dall’inclinazione della retta, dal suo coefficiente angolare.
