Funzioni concave e convesse: definizione
Qual è la differenza tra le funzioni concave e le funzioni convesse? Come capire se una funzione è concava o convessa? Scopri come usare le combinazioni lineari convesse per capire le proprietà della funzione che stai studiando!
Se parliamo di concavità e convessità, forse ti viene subito in mente la geometria. Anche nell’analisi matematica, quando si parla di funzioni, possiamo usare queste due parole.
Una funzione può essere, in un certo intervallo £$I$£, concava oppure convessa. Per capire di che tipo si tratta, dobbiamo fare ricorso al concetto di combinazione lineare.
Dal grafico di una funzione, possiamo subito vedere se una funzione è concava o convessa in un certo intervallo:
- la funzione è convessa se guarda verso l’alto
- la funzione è concava se invece guarda verso il basso
- Cos'è una combinazione lineare convessa
- Funzioni concave e convesse
- Esercizio svolto sulle funzioni convesse
Cos’è una combinazione lineare convessa
Prendiamo un insieme di elementi (tutti dello stesso tipo) £$x_{1},x_{2},\ldots,x_{n}$£ e un insieme di numeri reali £$\lambda_{1},\lambda_{2},\ldots,\lambda_{n}$£ tali che:
- £$ 0\le \lambda_{k} \le 1$£ per ogni £$k$£
- £$\lambda_{1}+\lambda_{2}+\ldots+\lambda_{n}=1$£
Allora, l’oggetto £$\lambda_{1}x_{1}+\lambda_{2}x_{2}+\ldots+\lambda_{n}x_{n}$£ è chiamato combinazione lineare convessa degli elementi £$x_{1},\ldots,x_{n}$£.
ESEMPIO: prendiamo due numeri reali [iol_placeholder type="formula" engine="katex" display="inline"]a Allora una combinazione lineare convessa di £$a$£ e £$b$£ è
£$\lambda_{a}a+(1-\lambda_{a})b$£
con £$\lambda_{a} \in [0,1]$£. Cosa rappresenta? Al variare di £$\lambda_{a} \in [0,1]$£ la combinazione lineare convessa £$\lambda_{a}a+(1-\lambda_{a})b$£ rappresenta tutti i valori compresi nell’intervallo £$[a,b]$£.
Funzioni concave e convesse
Usiamo il concetto di combinazione lineare complessa per definire le funzioni convesse.
Una funzione £$f$£ è convessa in un intervallo £$I$£ se £$\forall a,b \in I, \forall t \in [0,1]$£ vale la disuguaglianza £$f((1-t)a+tb)\le (1-t)f(a)+tf(b)$£
Cosa significa? Analizziamo la disuguaglianza: a sinistra abbiamo la funzione valutata nel punto £$(1-t)a+tb$£ che è sicuramente un punto compreso tra £$a$£ e £$b$£ perché, al variare di £$t \in [0,1]$£, è proprio la combinazione convessa di £$a$£ e £$b$£. A destra invece, abbiamo la combinazione convessa dei valori £$f(a)$£ e £$f(b)$£.
Quindi al variare di £$t$£ abbiamo tutti i punti compresi tra £$f(a)$£ e £$f(b)$£. Quindi una funzione è convessa in un intervallo £$I$£ se comunque presi due punti £$a,b$£ all’interno dell’intervallo, il grafico della funzione sta sotto il segmento che unisce i punti £$(a;f(a))$£ e £$(b;f(b))$£.
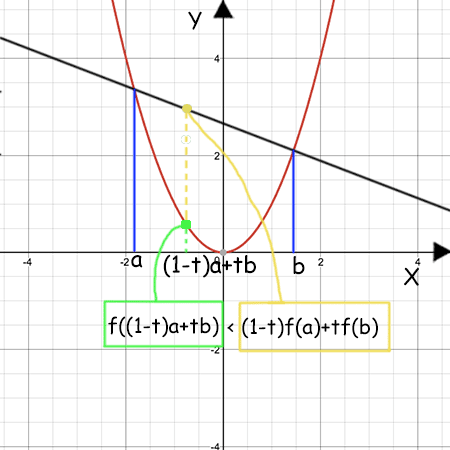
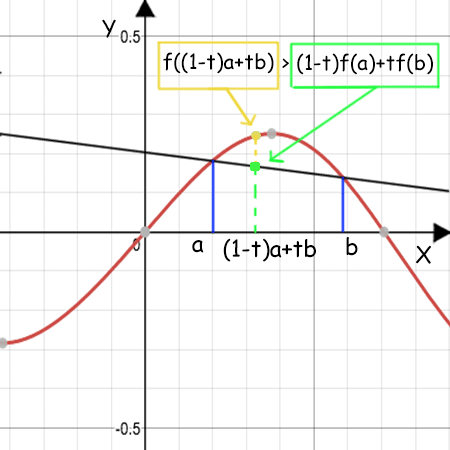
Una funzione £$f$£ è concava in un intervallo £$I$£ se £$\forall a,b \in I, \forall t \in [0,1]$£ vale la disuguaglianza £$f((1-t)a+tb)\ge (1-t)f(a)+tf(b)$£
Quindi una funzione è concava se il suo grafico sta sopra il segmento che unisce i punti £$(a;f(a))$£ e £$(b;f(b))$£.
Esercizio svolto sulle funzioni convesse
Consideriamo la funzione £$f(x)=x^2-1$£ nell’intervallo £$I=[0,2]$£. Questa funzione è concava o convessa nell’intervallo £$I$£?
Per rispondere, costruiamo la combinazione convessa di due punti [iol_placeholder type="formula" engine="katex" display="inline"]x,y \in [0,2], x
Sappiamo che la funzione è convessa se vale la disuguaglianza £$f((1-t)x+ty)\le (1-t)f(x)+tf(y)$£. Dobbiamo quindi calcolare le quantità a sinistra e a destra del segno di disuguaglianza e verificare se è vera oppure no.
- a sinistra abbiamo £$f((1-t)x+ty)=[(1-t)x+ty]^2-1=(1-t)^2x^2+t^2y^2+2t(1-t)xy-1$£
- a destra abbiamo £$(1-t)f(x)+tf(y)=(1-t)(x^2-1)+t(y^2-1)=(1-t)x^2+ty^2-1$£
Ora confrontiamole! Vediamo se vale la disuguaglianza per ogni £$x,y \in [0,2]$£ e per ogni £$t \in [0,1]$£:
£$(1-t)^2x^2+t^2y^2+2t(1-t)xy-1 \le (1-t)x^2+ty^2-1 \to$£ £$ x^2[(1-t)^2-(1-t)]+y^2(t^2-t)+2xy(t-t^2)\le 0 \to$£ £$x^2(t^2-t)+y^2(t^2-t)-2xy(t^2-t)\le 0 $£
dove abbiamo cambiato il segno nell’ultimo addendo per avere lo stesso fattore £$(t^2-t)=t(t-1)$£. Ora raccogliamo proprio questo fattore:
£$t(t-1)(x^2+y^2-2xy)\le 0 \to t(t-1)(x-y)^2 \le 0 $£
Vediamo che il prodotto £$t(t-1)$£ è minore o uguale di £$ per ogni [iol_placeholder type="formula" engine="katex" display="inline"]t \in [0,1]$£, mentre £$(x-y)^2 \ge 0$£ perché è un quadrato. Quindi la disuguaglianza è sempre verificata. Allora possiamo dire che la funzione £$f(x)=x^2-1$£ è convessa nell’intervallo £$[0,2]$£
