Il Pi Greco: lunghezza della circonferenza e area del cerchio
Ora che è chiara la differenza tra cerchio e circonferenza, impariamo come misurare la lunghezza della circonferenza e l’area del cerchio.
Esiste un numero speciale che si chiama Pi Greco (π): è molto importante perchè ci aiuta a fare tanti calcoli utili con i cerchi. Ad esempio, possiamo scoprire quanto è lunga la ruota della bicicletta o quanta pizza c’è in una pizza grande!
Se la circonferenza è il contorno del cerchio, ovvero il suo perimetro, possiamo misurare la sua lunghezza? Certo che sì! Per farlo dobbiamo servirci proprio del Pi Greco. Anche il cerchio è una figura piana: come facciamo a calcolare la sua area? Scopri la formula per calcolare l’area del cerchio. Non ti dimenticare del Pi greco!
Scopri a cosa serve questo Pi greco e impara la formula per trovare la lunghezza di una circonferenza e l’area del cerchio!
- Il contorno del cerchio
- Cos'è il Pi Greco
- Misurare la circonferenza
- Le formule inverse della circonferenza
- La superficie del cerchio
- Come calcolare l'area del cerchio
Il contorno del cerchio

Il cerchio non è un poligono: non è delimitato da una linea spezzata chiusa, ma da una circonferenza.
Sappiamo che la circonferenza è la linea formata da tutti i punti che si trovano alla stessa distanza da un punto chiamato centro della circonferenza.
Possiamo calcolare il perimetro di tutti i poligoni, possiamo fare lo stesso anche per il cerchio? Per misurare il perimetro di un cerchio, dobbiamo misurare la circonferenza.
Come misuriamo la lunghezza della circonferenza?
Cos’è il Pi Greco

Per misurare la lunghezza di una circonferenza, dobbiamo conoscere un numero particolare che si chiama Pi Greco.
Indichiamo il Pi Greco con il simbolo £$ \pi $£. Vale circa 3,14 e rappresenta il rapporto tra la lunghezza della circonferenza e il diametro di una circonferenza. Diciamo “circa 3,14" perchè in realtà continua con tanti altri numeri dopo la virgola. È un numero che non finisce mai e non ha un pattern che si ripete!
Prova a prendere qualcosa di rotondo: misura la lunghezza della circonferenza e la lunghezza del diametro. Poi calcola questa divisione:
lunghezza circonferenza : lunghezza diametro
Vedrai che il risultato di questa divisione sarà sempre un numero vicino a 3,14. Il risultato sarà tanto più preciso, quanto sarai preciso tu nel prendere le misure.
Pi greco è sempre lo stesso, non importa quali siano le dimensioni dell’oggetto che stiamo misurando.
Misurare la circonferenza
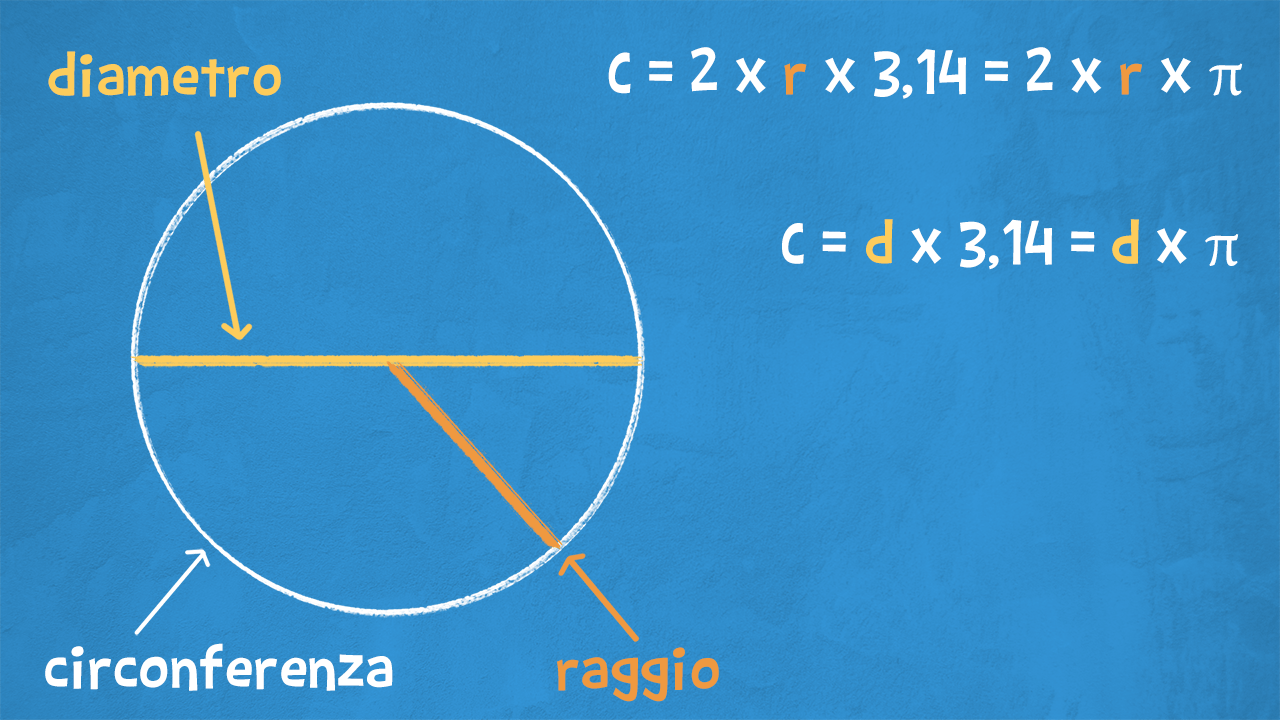
Come facciamo a calcolare la lunghezza di una circonferenza se conosciamo solo il suo raggio o il suo diametro?
Se conosciamo il diametro d, possiamo calcolare la lunghezza della circonferenza C in questo modo:
C = d x 3,14 = d x £$ \pi $£
Questo significa che servono 3,14 diametri per ricoprire una circonferenza.
Se conosciamo il raggio r, possiamo calcolare la lunghezza della circonferenza C così:
C = 2 x r x 3,14 = 2 x r x £$ \pi $£
Le formule inverse della circonferenza
È possibile ricavare la lunghezza del raggio o del diametro di una circonferenza conoscendo solo la sua lunghezza? Sì! Basta utilizzare le formule inverse, cioè “tornare indietro" a partire dalla misura della circonferenza.
Chiamiamo la circonferenza C, il raggio r e il diametro d. Allora:
C = 2 x r x £$ \pi $£
r = C : 2 : £$ \pi $£
d = C : £$ \pi $£
La superficie del cerchio
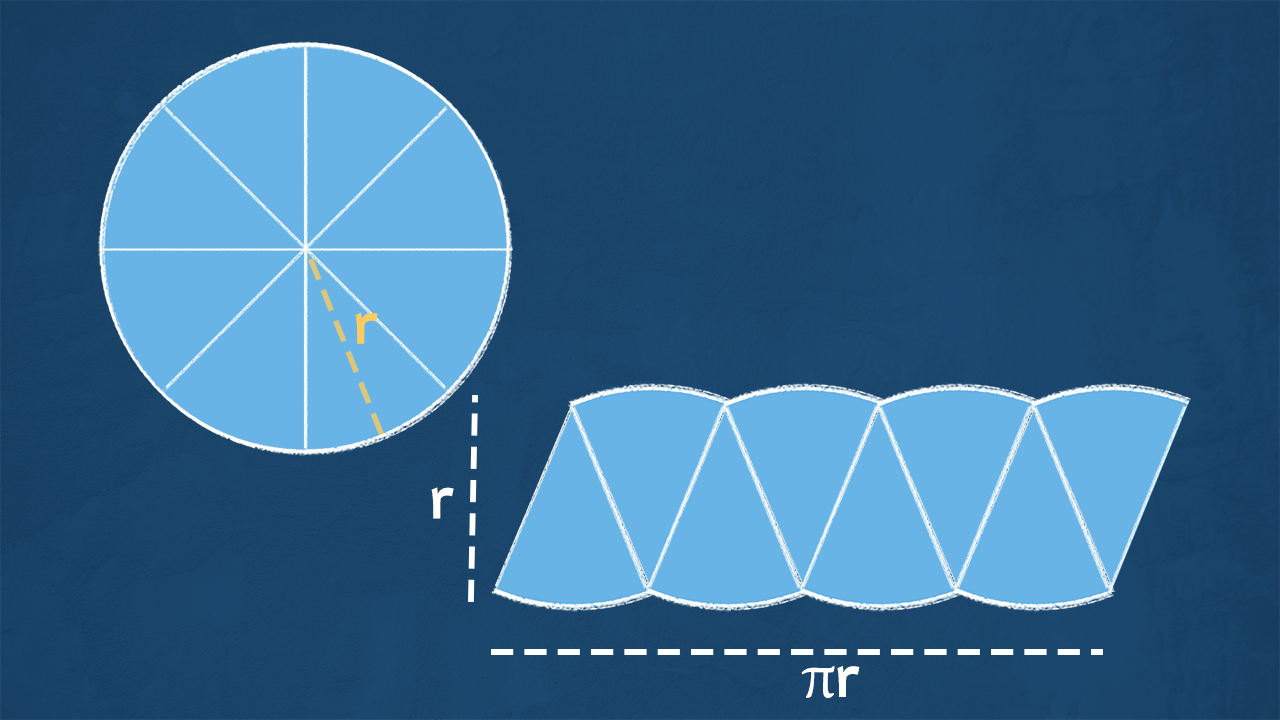
Anche il cerchio è una figura piana, pur non essendo un poligono.
Possiamo calcolare la sua area come abbiamo imparato a calcolare le aree dei poligoni.
Proviamo a ritrovare una figura che conosciamo già molto bene: affettiamo il cerchio in settori circolari tutti uguali. Se li mettiamo uno a fianco all’altro, riusciamo a formare una sorta di parallelogramma.
Ricordi come calcolare l’area di un parallelogramma? Basta moltiplicare la base e l’altezza. Proviamo a ritrovare la misura della base e dell’altezza di questo parallelogramma che abbiamo ricostruito: l’altezza è uguale al raggio del cerchio, la base invece corrisponde alla metà della circonferenza.
Allora possiamo calcolare l’area del cerchio così:
A = (C : 2) x r
Come calcolare l’area del cerchio

Abbiamo conosciuto un numero particolare, il Pi greco. Può esserci utile anche per calcolare l’area di un cerchio?
Il Pi greco comparirà ogni volta che avremo a che fare con cerchio e circonferenza, dovremo farci l’abitudine.
Per calcolare l’area di un cerchio possiamo usare la formula:
A = r£$^2$£ x £$ \pi $£
L’area di un cerchio è uguale a circa tre volte l’area di un quadrato con il lato uguale al raggio del cerchio.
