Rappresentare le isometrie: come si fa una traslazione
Oggi esploreremo alcuni concetti affascinanti della geometria: la traslazione, il vettore spostamento e le isometrie. Questi termini possono sembrare complicati, ma con un po’ di spiegazione e alcuni esempi, saranno molto facili da capire.
La traslazione indica uno spostamento nello spazio. Scopri cos’è il vettore traslazione: indica la direzione, il verso e la misura dello spostamento.
Capire la traslazione, il vettore spostamento e le isometrie ci aiuta a comprendere meglio come le figure si muovono e cambiano posizione nello spazio. Questi concetti sono fondamentali per risolvere problemi di geometria e per capire meglio il mondo intorno a noi.
Vediamo insieme come riconoscere e rappresentare una traslazione!
- Definizione di spostamento per spiegare la traslazione
- Traslazioni e isometrie: cosa sono
- Come fare una traslazione
Definizione di spostamento per spiegare la traslazione

Possiamo spostarci in tutte le direzioni: in avanti, all’indietro, andando dritto oppure muovendoci in obliquo. Questo spostamento è una trasformazione geometrica che si chiama traslazione.
Il vettore spostamento è uno strumento che ci aiuta a descrivere la traslazione. Un vettore è come una freccia che mostra la direzione e la distanza del movimento. Per esempio, se spostiamo una figura 3 passi a destra e 2 passi in alto, possiamo usare un vettore per mostrare questo spostamento.
Traslazioni e isometrie: cosa sono
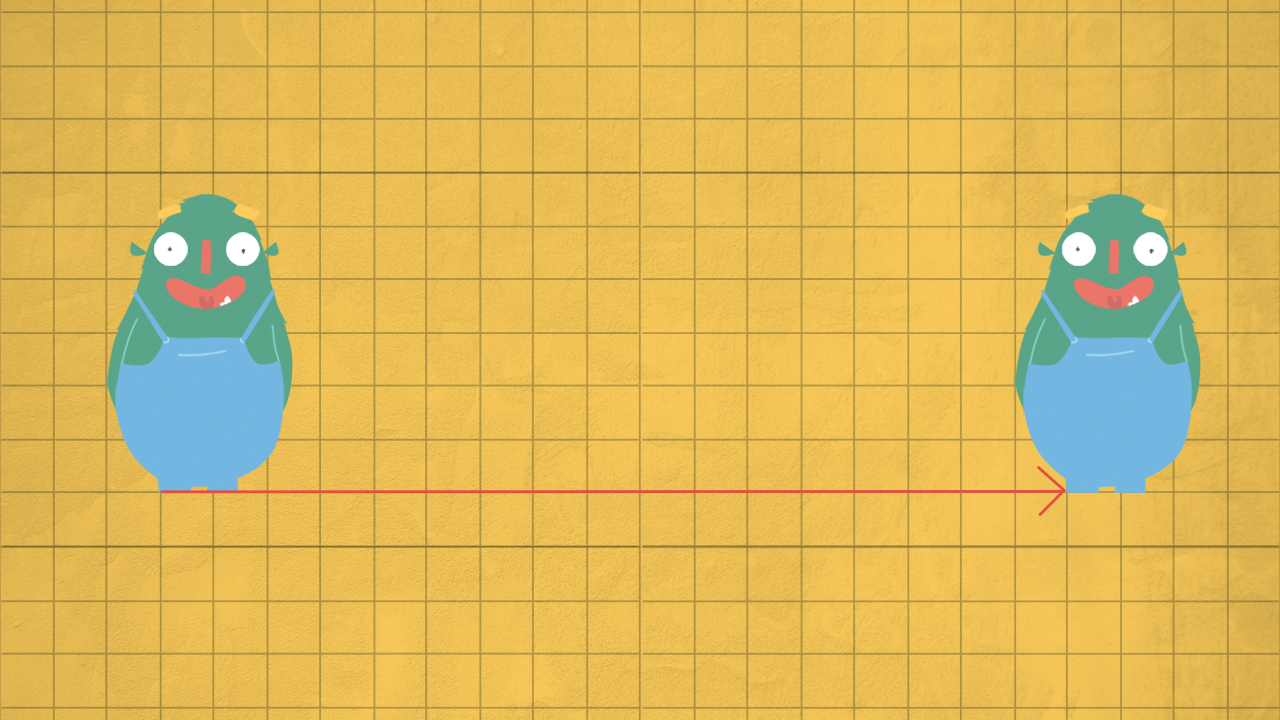
Anche le traslazioni, come le simmetrie e le rotazioni, sono trasformazioni geometriche che non cambiano la forma della figura, ma solo la sua posizione: sono isometrie.
Per individuare una traslazione occorre conoscere:
- la direzione dello spostamento
- il verso dello spostamento
- la misura dello spostamento
La freccia che individua una traslazione si chiama vettore.
Come fare una traslazione
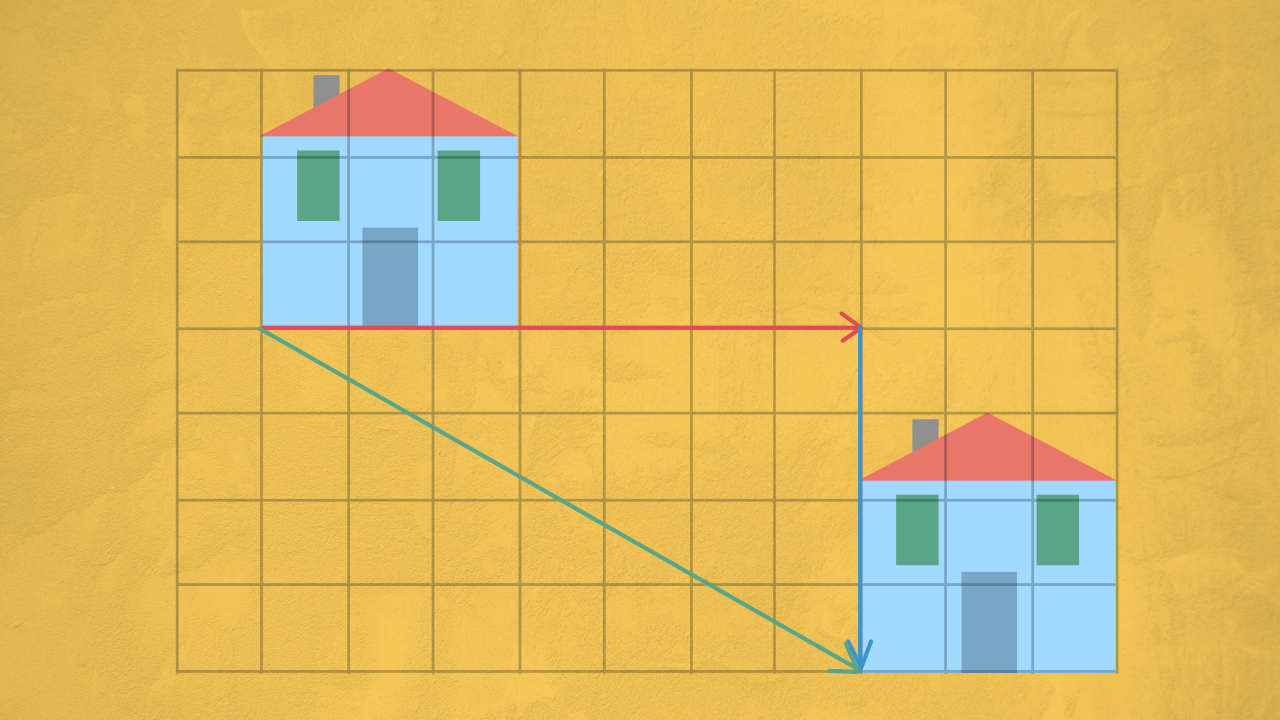
Il vettore che rappresenta la traslazione è una freccia che ci dà tutte le informazioni. È facile rappresentare una traslazione quando la freccia è orizzontale o verticale, ma come fare quando è obliqua?
Possiamo scomporre una traslazione rappresentata da un vettore obliquo in due traslazioni: la componente orizzontale e quella verticale, in modo da combinare due spostamenti per ottenere lo spostamento risultante.
Passo 1: Disegna la figura
Prima di tutto, disegniamo la figura che vogliamo traslare. Per esempio, possiamo disegnare un triangolo su un foglio di carta o su una griglia.
Passo 2: Scegli il vettore spostamento
Il vettore ha due componenti:
- Direzione orizzontale (x): quanti passi fare verso destra (se positivo) o verso sinistra (se negativo).
- Direzione verticale (y): quanti passi fare verso l’alto (se positivo) o verso il basso (se negativo).
Ad esempio, scegliamo un vettore spostamento (3, 2), il che significa spostare la figura 3 passi a destra e 2 passi in alto.
Passo 3: Applica il vettore spostamento
Ora applichiamo il vettore spostamento a ogni punto della figura.
- Prendiamo il primo punto del triangolo e spostiamolo 3 passi a destra e 2 passi in alto.
- Ripetiamo lo stesso per ogni punto del triangolo.
- Colleghiamo i nuovi punti per disegnare la figura traslata.
Passo 4: Verifica il risultato
Dopo aver applicato il vettore spostamento a tutti i punti e aver disegnato la nuova figura, confrontiamo la figura originale con quella traslata. Dovrebbero avere la stessa forma e dimensione, ma trovarsi in posizioni diverse.
E adesso tocca a te! Prova a spostare altre figure usando diversi vettori spostamento e vedrai come si muovono senza cambiare forma o dimensione. Buon divertimento con le traslazioni!
