Riduzioni e ingrandimenti in scala: come usarli
Quante volte ti sei chiesto come rappresentare una mappa? Basta fare una riduzione in scala! Al contrario, gli ingrandimenti in scala possono essere utili per riuscire a vedere i dettagli nelle figure più piccole. Scopri come funzionano!
Scala 1 : 5… cosa significa? 1 cm rappresentato sulla mappa corrisponde a 5 cm nella realtà. Dai un’occhiata alle cartine geografiche! Utilizza la riduzione in scala per provare a fare una piantina in scala della tua classe!
Come funzionano gli ingrandimenti? Usiamo la scala al contrario: scala 6 : 1 indica che 6 cm sull’ingrandimento corrispondono ad un solo cm nella realtà.
Scopri come cambiano aree e perimetri delle figure ingrandite o rimpicciolite in scala. Segui tutte le regole e prova a risolvere gli esercizi!
Le riduzioni in scala

Hai mai notato quella scritta nelle cartine geografiche? Scala 1 : 200. Cosa significa?
Per disegnare le mappe, le cartine geografiche, le piantine, le carte stradali, ecc… occorre ridurre le misure, cioè fare una riduzione in scala. Questo numero indica di quanto le abbiamo ridotte!
La scala 1 : 200 ci dice che un centimetro nella mappa corrisponde a 200 centimetri nella realtà. Se misuriamo 4 cm sulla mappa, sappiamo che nella realtà corrispondono a 4 x 200 = 800 cm, cioè 8 metri.
Il rapporto tra le misure reali e le misure rappresentate sulla mappa è costante ed è uguale a 200: infatti 800 cm : 4 cm = 200.
Per individuare la scala di riduzione di una figura, basta calcolare il rapporto tra i lati prima e dopo la riduzione.
Osserva l’immagine: quale scala di riduzione è stata applicata?
Gli ingrandimenti

L’ingrandimento in scala funziona all’opposto della riduzione: quello che non cambia è che resta ancora fisso il rapporto tra i lati della figura prima e dopo l’ingrandimento.
Per esempio, l’ingrandimento di scala 4 : 1 indica che un centimetro nella realtà corrisponde a 4 centimetri nell’ingrandimento. Se nell’ingrandimento il lato di una figura misura 28 cm, nella realtà era di 28 cm : 4 cm = 7 cm.
Osserva l’immagine: quale scala di ingrandimento è stata applicata?
Come variano perimetri e aree in scala
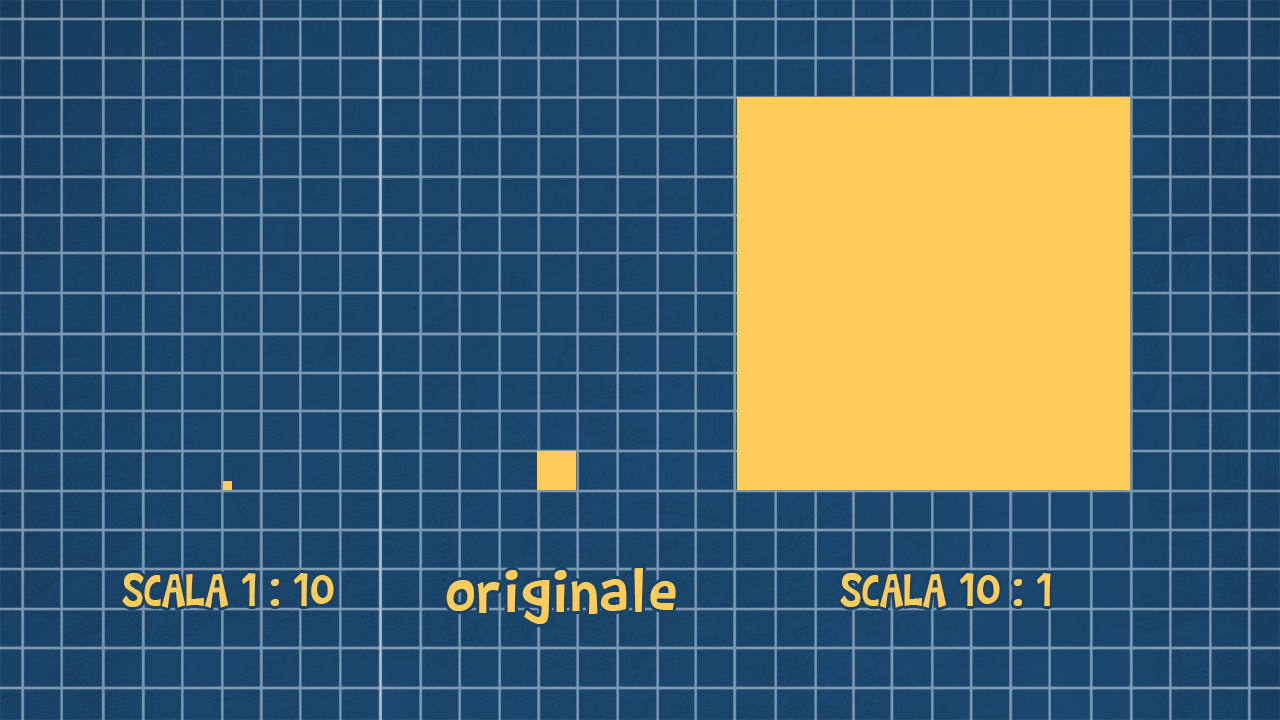
In caso di riduzione (o ingrandimento) ovviamente variano anche perimetri e aree dei poligoni.
Applicando una riduzione di scala 1 : 10, i lati della figura di partenza saranno 10 volte più piccoli. Di conseguenza anche il perimetro sarà 10 volte più piccolo!
Nel caso di un ingrandimento in scala 5 : 1, i lati della figura ingrandita sono 5 volte più grandi, quindi anche il perimetro è 5 volte più grande.
Per le aree funziona diversamente! Consideriamo la figura a cui è applicata una scala di riduzione 1 : 10: i lati sono 10 volte più piccoli, ma come è cambiata l’area? L’area di una figura ridotta in scala varia con una scala quadratica, sarà in scala 1 : (10 x 10), cioè in scala 1 : 100.
Analogamente funziona per gli ingrandimenti: se l’ingrandimento è in scala 5 : 1, l’area si ingrandirà in scala quadratica (5 x 5) : 1, cioè 25 : 1.
Osserva le immagini e misura le aree con i quadretti per verificarlo!
