Pi Greco: cos'è, definizione ed esercizi

Pi greco, spesso rappresentato con il simbolo greco π, è un numero che ha affascinato matematici, fisici e filosofi per millenni. È uno dei più noti numeri irrazionali, che significa che non può essere espresso come un rapporto esatto tra due numeri interi, e la sua sequenza di cifre decimali non termina né si ripete.

Ma cos’è esattamente il π? Come si calcola e perché occupa un posto così speciale nel mondo della matematica e della scienza? In questo articolo esploreremo la sua storia e scopriremo come viene utilizzato nei calcoli scientifici e nella vita quotidiana.

Dall’antichità ai giorni nostri, infatti, il π continua a giocare un ruolo cruciale in molte aree della matematica e delle scienze, dal calcolo del perimetro e dell’area di un cerchio alla descrizione del comportamento di onde fisiche. Scopriamolo insieme!

• La storia del Pi Greco
• Come si calcola il Pi Greco
• Come memorizzare le cifre del Pi Greco
• Esercizio con il Pi Greco

La storia del Pi Greco

Il Pi Greco era stato individuato già da Babilonesi e Egiziani. Ovviamente questi non trovarono il valore esatto di £$ \pi $£, ma riuscirono a trovare delle approssimazioni utili nella loro quotidianità.

I Babilonesi nel XX secolo a.C. trovarono per £$ \pi $£ il valore di £$ \dfrac{25}{8} = 3{,}125 $£. In questo modo scoprirono che la lunghezza della circonferenza è poco più di tre volte il suo diametro.

Più tardi, intorno al 1700 a.C., nel famoso papiro di Rhind, l’egiziano Ahmes affermò che l’area di un cerchio di diametro £$ d $£ si otteneva dalla formula £$ A = \left( d – \dfrac d9 \right)^2 $£. Se proviamo a svolgere il conto per un cerchio di raggio £$ 1 $£, troviamo il valore di £$ \pi $£ con una sola cifra decimale esatta, cioè £$ 3{,}1605 $£.

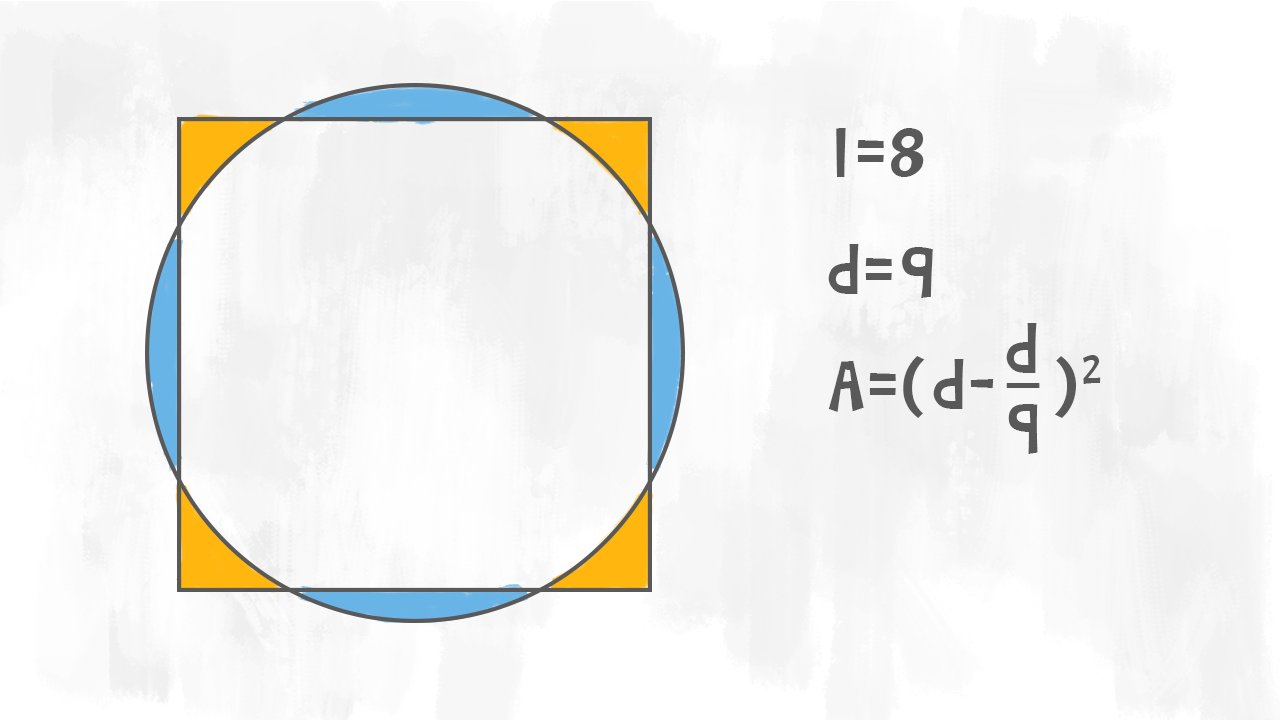
Nel quarto secolo a.C. molti pensatori greci si impegnarono nello studio della misura del cerchio. Il primo a tentare di trovare il rapporto tra un cerchio e un quadrato fu Anassagora. In seguito Archimede realizzò una vera e propria dimostrazione per calcolare un valore di £$ \pi $£ più corretto. Inscrivendo e circoscrivendo alla circonferenza unitaria lo stesso poligono regolare, riuscì a trovare le prime cifre decimali di £$ \pi $£. Più aumentava i lati dei poligoni regolari, più il valore delle loro aree si avvicinava a quello di £$ \pi $£. Archimede ingabbiò il valore di £$ \pi $£ tra due numeri, i numeri guardiani: £$ 3 + \dfrac{10}{71} costante di Archimede.

Nel 400 d.C. l’astronomo cinese Tsu Chung-Chi approssimò [iol_placeholder type="formula" engine="katex" display="inline"] \pi $£ con la frazione £$ \dfrac{355}{113} \simeq 3{,}14159292… $£, con sei cifre decimali esatte!

Isaac Newton nel 1665 arrivò a calcolare un’approssimazione di £$ \pi $£ fino alla sedicesima cifra decimale.

Nel diciottesimo secolo William Jones e Eulero introdussero il simbolo £$ \pi $£ per indicare questo numero. Finalmente nel 1761 Johann Lambert dimostrò che £$ \pi $£ è un numero irrazionale, quindi un numero che non può essere scritto come rapporto tra due numeri interi.

Con i moderni calcolatori siamo ormai arrivati a conoscere migliaia, milioni, miliardi di cifre decimali di £$ \pi $£.

Un giapponese è riuscito a recitare a memoria ben centomila cifre di £$ \pi $£. Chissà se con qualche trucchetto puoi riuscire a stabilire un nuovo record! 😉

Come si calcola il Pi Greco

Il valore di π è strettamente legato alla geometria del cerchio. Il pi greco è, per definizione, il rapporto tra la circonferenza di un cerchio e il suo diametro. Questa relazione sembra semplice, ma la realtà è che π è un numero irrazionale, il che significa che non può essere rappresentato in modo esatto da un numero decimale finito o da una frazione.

Quindi, come calcoliamo π? In verità, per la maggior parte delle applicazioni pratiche, conoscere π con una precisione di poche cifre decimali è più che sufficiente. Ad esempio, per la maggior parte dei calcoli scientifici, π è approssimato a 3,14.

Tuttavia, il calcolo di π con precisione è una sfida che ha affascinato gli umani per millenni. I matematici dell’antica Babilonia, ad esempio, avevano calcolato π come 3,125. Gli antichi Egizi lo avevano approssimato a 3,16. Più tardi, Archimede di Siracusa ha sviluppato un metodo per avvicinarsi sempre più al valore di π, concludendo che si trova tra 3 1/7 e 3 10/71.

Nell’era del computer, i matematici hanno calcolato π a trilioni di cifre decimali. Questo è fatto più per il gusto della sfida che per una necessità pratica, ma dimostra le sorprendenti profondità e complessità che si nascondono dietro questo apparentemente semplice numero.

Come memorizzare le cifre del Pi Greco

È più facile imparare a memoria una serie di numeri oppure una poesia, con rime ben disposte e un significato preciso?

Probabilmente, anche se sei un amante della matematica e dei numeri, preferisci la seconda soluzione. Le poesie, le parole in generale, possono aiutarci a memorizzare procedimenti, cifre, tabelline… Esiste un trucco anche per memorizzare le cifre di £$ \pi $£.

Molti si sono cimentati a scrivere semplici componimenti per memorizzare le prime cifre di £$ \pi $£. Come hanno fatto? Basta associare ad ogni parola un numero. Una parola di tre lettere indicherà il numero 3, una di quattro lettere indica il numero 4, una di una sola lettera indica il numero 1… E così via! Combinando le parole giuste, otteniamo delle semplici poesie che possono aiutarci a ricordare le cifre decimali di £$ \pi $£.

Vediamone qualcuna!

La scuola

3. £$ \ $£ 1 £$ \ $£ 4 £$ \ $£ 1 £$ \quad $£ 5 £$ \quad $£ 9 £$ \quad \quad $£ 2
Tra i muri e amata compagnia si

6 £$ \quad \quad $£ 5 £$ \quad $£ 3 £$ \quad $£ 5 £$ \quad $£ 8 £$ \quad \quad \ $£ 9 £$ \quad \quad \ $£ 7
impara molto con tanta allegria, simpatica maestra

9 £$ \quad \quad \ $£ 3 £$ \ \ $£ 2 £$ \ \ $£ 3 £$ \quad $£ 8
costringe con la sua severità.

Pi Greco

3. £$ \ $£ 1 £$ \quad $£ 4 £$ \ $£ 1 £$ \quad $£ 5 £$ \quad \quad $£ 9 £$ \quad $£ 2
Ave o Roma o Madre gagliarda di

6 £$ \quad \ $£ 5 £$ \quad $£ 3 £$ \quad $£ 5 £$ \quad $£ 8 £$ \quad \quad \ $£ 9
latine virtù che tanto luminoso splendore

£$ \quad $£ 7 £$ \quad \quad $£ 9 £$ \quad \ $£ 3 £$ \ \ $£ 2 £$ \ $£ 3 £$ \quad $£ 8
prodiga spargesti con la tua saggezza.

Queste poesie possono aiutarci a ricordare le prime 19 cifre di £$ \pi $£. Ci sono poi racconti che aiutano a ricordare fino a 400 cifre di £$ \pi $£. Prova anche tu a scrivere un racconto o una poesia per memorizzare più cifre possibili!

Esercizio con il Pi Greco

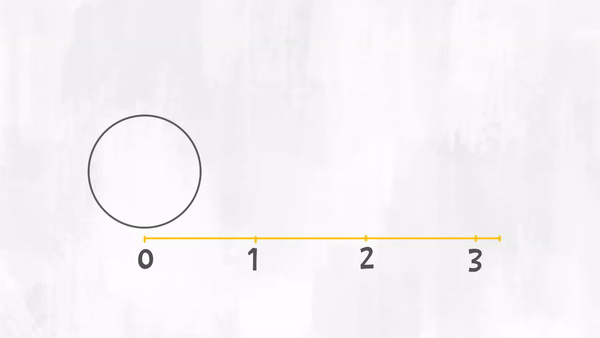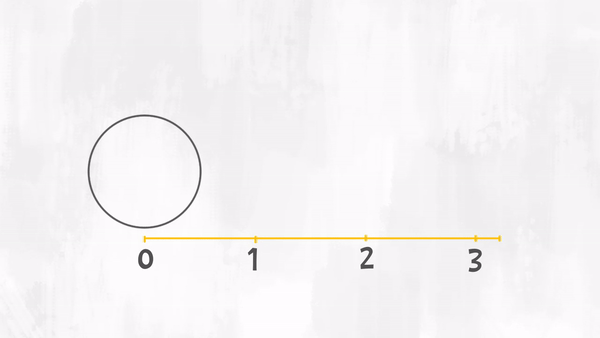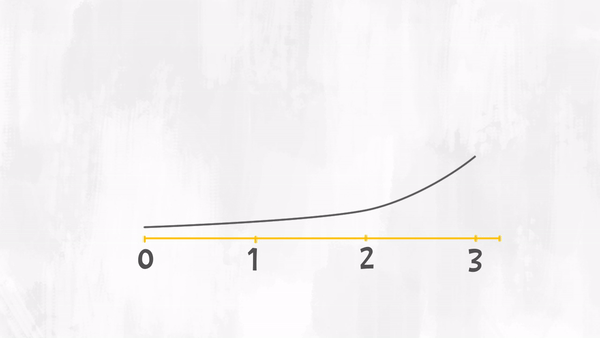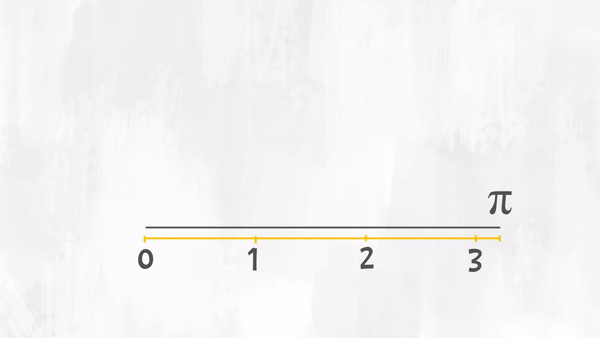
Per capire come interviene pi greco nel calcolo della misura di una circonferenza, possiamo misurare la circonferenza di una bottiglia (o di un bicchiere, o di qualsiasi cosa che abbiamo una sezione circolare) con l’aiuto di un filo. Con un altro filo, possono poi misurare la lunghezza del diametro e verificare quante volte il diametro “sta" nella lunghezza della circonferenza.
Un po’ come abbiamo fatto qui! Quale risultato otteniamo? Vediamo che la circonferenza misura più di 3 diametri, ma meno di quattro, cioè £$ \pi \text{ diametri} $£.

Sappiamo che il Pi Greco è un numero irrazionale, quindi un numero che non possiamo rappresentare come rapporto tra due numeri interi. Non è facile capire la differenza tra un numero razionale e un numero irrazionale. Allora proviamo a visualizzarla! Realizziamo un cartellone in cui rappresentiamo tutti i numeri con colonnine verticali su fogli a quadretti: il 3 corrisponde a 3 quadretti, il numero 1 corrisponde ad un quadretto, il 4 a 4 quadretti… E così via. Rappresentiamo ogni numero è rappresentato con una colonna di colore diverso. Poi mettiamo di fianco tutte le colonnine realizzate, nell’ordine giusto per formare le cifre decimali di £$ \pi $£ (qui trovi le prime 100 mila cifre). In questo modo vediamo come le cifre decimali di Pi Greco non presentino alcuna regolarità.

Visto che i numeri che formano £$ \pi $£ non sono per niente regolari, possiamo scoprire diverse curiosità. Esistono diversi siti in cui trovare la posizione della propria data di nascita all’interno delle cifre di Pi Greco (ad esempio questo sito permette di ricercare la propria data di nascita tra le prime 4 194 166 cifre del Pi Greco). Vediamo che riusciamo a trovare praticamente tutte le date di nascita espresse nel formato GG/MM/AA.

Altrimenti possiamo provare a cercare altri “numeri famosi", come quelli della successione di Fibonacci. Su questo sito possiamo ricercare tutte le stringhe di numeri che vogliamo, anche il nostro numero di telefono! Il programma ci dirà se è riuscito a trovare la stringa inserita tra le prime 200 000 000 cifre di Pi Greco.

A cosa serve tutto questo? Sempre a rimarcare il fatto che le cifre decimali di Pi Greco sono assolutamente casuali, senza uno schema preciso, in quanto pi greco è un numero irrazionale. Provate a creare delle sfide! Vedrete che i numeri fino a 6 cifre si trovano praticamente sempre, i numeri più lunghi invece sono più difficili da trovare tra le cifre di £$ \pi $£. Ci ricolleghiamo quindi alla probabilità: facendo diverse prove, realizziamo che c’è una probabilità del 100% di trovare stringhe di 5 numeri tra le prime 200 000 000 cifre decimali di pi, e vediamo che questa probabilità diminuisce man mano che sia aumenta la lunghezza delle stringhe di numeri.