I tipi di angolo: come si classificano
Gli angoli sono ovunque. Osserva qualsiasi struttura, oggetto o modello matematico, e vi troverai quasi sicuramente un angolo nascosto o più visibile. Ma cosa sono esattamente gli angoli? E come possiamo classificarli e sfruttare le loro proprietà in geometria?
Gli angoli, in termini basilari, sono una misura della rotazione o dell’inclinazione tra due raggi (o segmenti) che si incontrano in un punto chiamato vertice. Rappresentano una porzione dello spazio che li circonda e sono un concetto fondamentale nella matematica in generale e nella geometria in particolare. Possono essere acuti, retti, ottusi o piatti, a seconda della loro ampiezza. Ognuno di questi tipi di angoli ha caratteristiche e proprietà proprie che impareremo insieme in questo articolo. Oltre a queste classificazioni base, ci sono angoli complementari, supplementari ed esplementari.
Pronti? Scopriamo insieme le caratteristiche di questi fondamentali elementi geometrici!
- Che cos'è un angolo
- Come misurare gli angoli
- Gli angoli convessi e concavi
- Le tipologie di angoli particolari
- Confronto e somma tra angoli
- Angoli complementari, supplementari, esplementari
- Esercizi con gli angoli
Che cos’è un angolo
Vediamo gli angoli tutti i giorni leggendo l’ora sull’orologio: le lancette sono i lati dell’angolo e il centro dell’orologio è il vertice. Ma che cosa sono gli angoli?
Un angolo è ciascuna delle due parti di piano comprese tra due semirette che hanno la stessa origine. Le due semirette sono i lati dell’angolo, l’origine comune, invece, è il vertice dell’angolo.
Misuriamo gli angoli utilizzando i gradi e li indichiamo con le lettere dell’alfabeto greco, come £$ \alpha, \beta, \gamma … $£. Oppure possiamo anche utilizzare tre punti: uno per ciascuna delle due semirette e uno per il vertice. Per esempio scriviamo £$ A\widehat{O}B $£ l’angolo che ha vertice in £$ O $£: la lettera centrale in questa scrittura deve sempre essere il vertice.
Furono i babilonesi a suddividere per primi i cerchi in £$ 360 $£ parti, ciascuna delle quali era un angolo che misura un grado. I babilonesi utilizzarono questa suddivisione perché pensavano che i giorni dell’anno fossero £$ 360 $£. Più avanti si scoprì che i giorni dell’anno sono £$ 365 $£, ma la suddivisione del cerchio in £$ 360 $£ parti rimase e continuò ad essere utilizzata per misurare gli angoli. È quello che chiamiamo sistema sessagesimale: £$ 1 $£ grado è la £$ 360 –$£esima parte di un cerchio, in ogni grado ci sono £$ 60 $£ primi e in ogni primo ci sono £$ 60 $£ secondi.
Come misurare gli angoli
Per misurare gli angoli utilizziamo uno strumento: il goniometro. Può essere di forma circolare (quindi è suddiviso in £$ 360 $£ parti uguali, cioè £$ 360^\circ $£), oppure semicircolare (suddiviso in £$ 180 $£ parti uguali, cioè £$ 180^\circ $£). Posizioniamo il centro del goniometro in corrispondenza del vertice dell’angolo in modo che lo £$ 0 $£ corrisponda al primo lato dell’angolo: guardiamo dove arriva il secondo lato per trovare la misura dell’angolo.
Per misurare gli angoli utilizziamo il sistema sessagesimale: un grado è la £$360-$£esima parte di un cerchio. Anche il grado ha i suoi sottomultipli: i primi e i secondi. In un grado ci sono £$ 60 $£ primi, in un primo ci sono £$ 60 $£ secondi. Non ti sembra di avere a che fare tutti i giorni con queste misure? Funzionano esattamente come i minuti e i secondi nelle misure di tempo! In un’ora abbiamo £$ 60 $£ minuti e in ogni minuto abbiamo £$ 60 $£ secondi, nello stesso modo:
£$ 1^\circ $£ si suddivide in £$ 60’ $£
£$ \quad 1’ $£ si suddivide in £$ 60’’ $£
Esempio: £$ \alpha = 49^\circ \ 20’ \ 15’’ \\ \beta = 89^\circ \ 59’ \ 60’’ = 89^\circ \ 60’ \ 00’’ = 90^\circ \ 00’ \ 00’’ $£
Gli angoli convessi e concavi
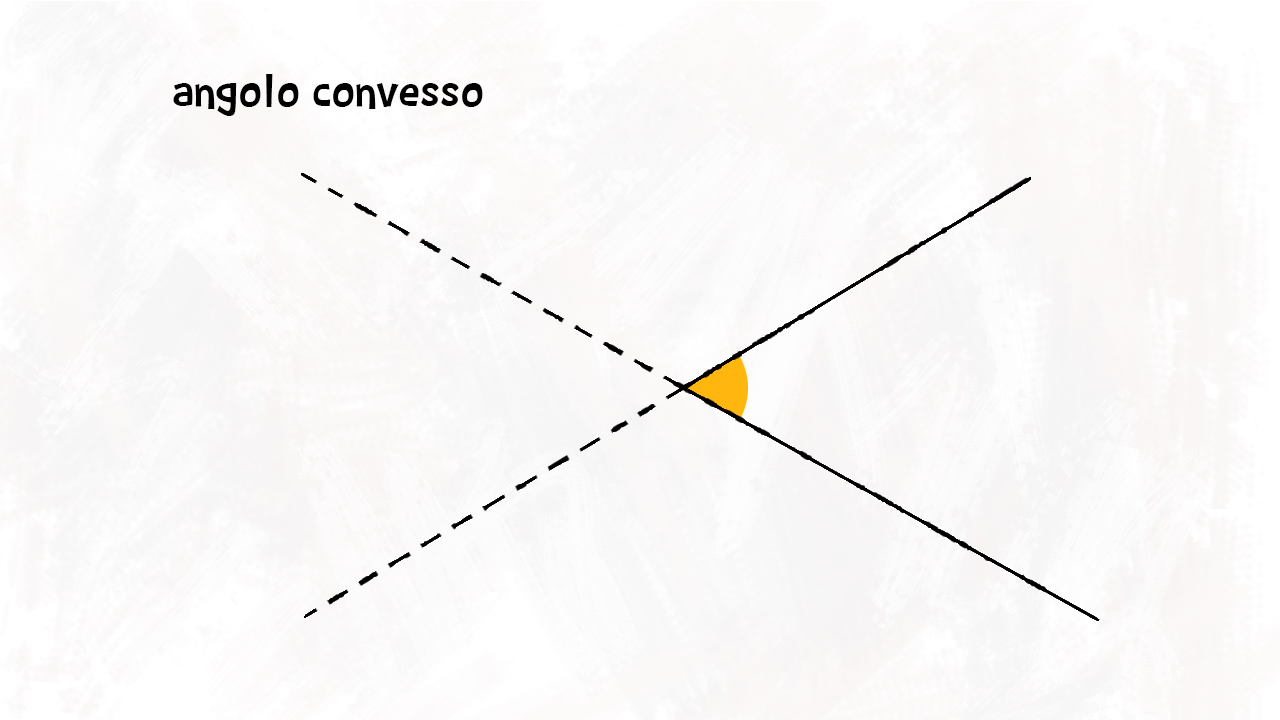
Angolo convesso £$ \alpha $£
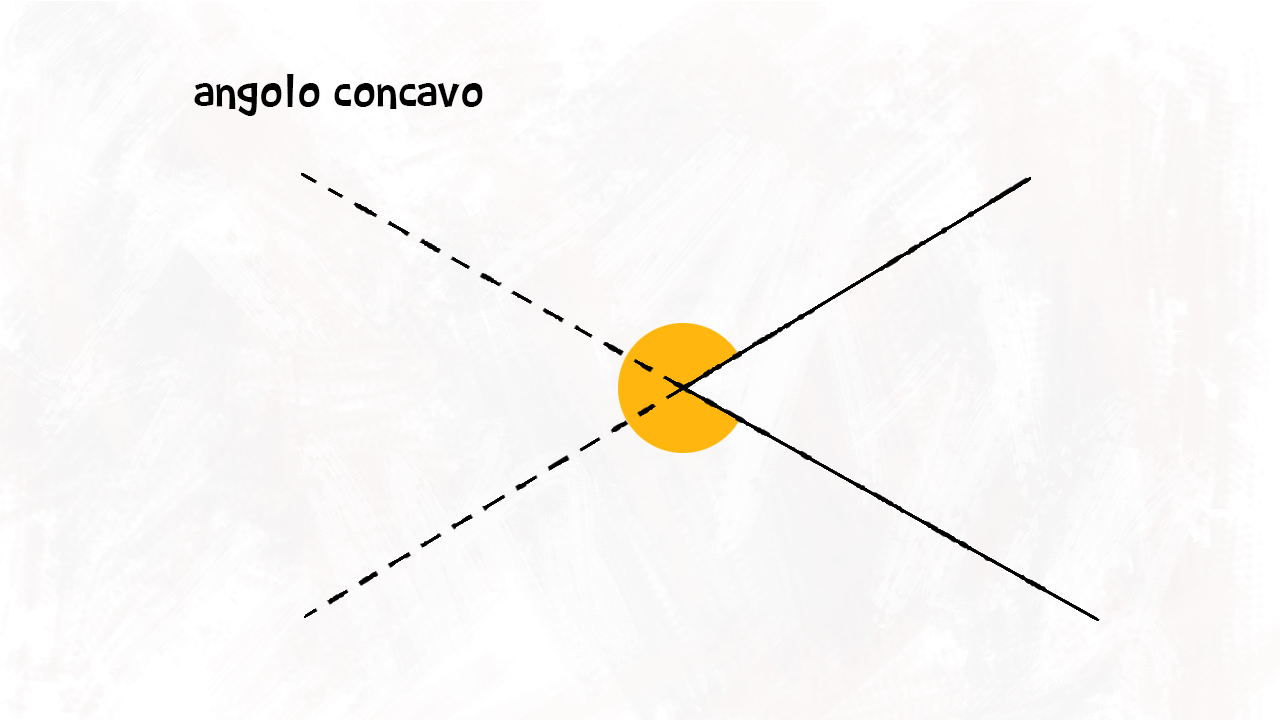
Angolo concavo £$ \beta $£
Abbiamo capito come si disegnano gli angoli. Ora possiamo iniziare a dare qualche altra definizione.
Un angolo è convesso se non contiene il prolungamento dei suoi lati. Per esempio l’angolo £$ \alpha $£ è un angolo convesso: se proviamo a prolungare i suoi lati, non sono all’interno dell’angolo.
L’angolo che contiene il prolungamento dei suoi lati, invece, è un angolo concavo. Per esempio l’angolo £$ \beta $£ è un angolo concavo: vediamo nell’immagine che il prolungamento dei suoi lati interseca l’angolo.
Solitamente sono convessi tutti gli angoli che misurano tra £$ 0^\circ $£ e £$ 180^\circ $£, sono concavi tutti gli angoli che misurano tra £$ 180^\circ $£ e £$ 360^\circ $£.
Le tipologie di angoli particolari
Identifichiamo gli angoli a partire da quanto misurano: ci sono però degli angoli che hanno un nome particolare perché hanno delle caratteristiche che li rendono unici.
L’angolo giro è l’angolo che misura £$ 360^\circ $£. Lo dividiamo a metà e troviamo l’angolo piatto che misura £$ 180^\circ $£. Se dividiamo l’angolo giro in quattro parti uguali, invece, troviamo l’angolo retto che misura £$ 90^\circ $£.
A partire dall’angolo retto possiamo riconoscere se un angolo è acuto o ottuso: un angolo ottuso è un angolo £$ \alpha $£ che ha misura £$$ 90^\circ angolo acuto, invece, è un angolo [iol_placeholder type="formula" engine="katex" display="inline"] \beta $$ che ha misura [iol_placeholder type="formula" engine="katex" display="inline"] 0 Gli angoli acuti e gli angoli ottusi sono tutti angoli convessi. In generali sono concavi gli angoli £$ \gamma $£ che hanno un’ampiezza [iol_placeholder type="formula" engine="katex" display="inline"] 180^\circ
Confronto e somma tra angoli
Possiamo confrontare due angoli per capire come variano le loro ampiezze. Ma come si fa? Come abbiamo già visto con i segmenti, per confrontare l’ampiezza di due angoli, dobbiamo sovrapporli facendo coincidere il vertice e un lato. Se anche l’altro lato coincide, i due angoli hanno la stessa ampiezza, quindi sono congruenti. Se il lato del secondo angolo cade all’interno del primo angolo, il secondo angolo sarà minore del primo; se invece il lato del secondo angolo cade all’esterno del primo angolo, il secondo angolo sarà maggiore del primo. Se due angoli hanno ampiezze diverse è maggiore l’angolo con ampiezza maggiore!
Dopo aver confrontato le ampiezze di due angoli, proviamo a sommarli. Per sommare due angoli, dobbiamo prima disegnarli in modo che siano consecutivi: hanno il vertice e un lato in comune; gli altri due lati sono da parti opposte rispetto al lato comune. L’ampiezza dell’angolo somma è uguale alla somma delle ampiezze dei due angoli.
Due angoli sono adiacenti se sono consecutivi e i due lati non comuni appartengono alla stessa retta.
Due angoli sono opposti al vertice quando i lati di uno sono il prolungamento dei lati dell’altro: i quattro angoli che si creano sono congruenti a due a due.
Angoli complementari, supplementari, esplementari
Quando la somma di due angoli dà un risultato particolare, questi due angoli possono essere:
- se la somma di due angoli è £$ 90^\circ $£, i due angoli sono complementari;
- se la somma è £$ 180^\circ $£, i due angoli sono supplementari;
- se la somma di due angoli è £$ 360^\circ $£, i due angoli sono esplementari.
Anche se non sappiamo la misura dei due angoli, il fatto che siano complementari, supplementari o esplementari, ci dà già un’informazione sulla loro somma. Questo può esserci utile per risolvere il problema!
Esercizi con gli angoli
Esercizio svolto: gli angoli supplementari
Esercizio svolto: i multipli e sottomultipli
Per sommare due angoli dobbiamo spostarli in modo che diventino consecutivi, cioè in modo che abbiano il vertice e un lato in comune. L’angolo che otteniamo in questo modo è la somma dei due angoli. Se la somma di due angoli consecutivi è £$ 180^\circ $£, allora i due angoli sono adiacenti.
Per sottrarre due angoli di ampiezza diversa, dobbiamo sovrapporli in modo che abbiano un vertice e un lato in comune. L’angolo che si ottiene è la differenza tra i due angoli. Se i due angoli invece sono congruenti, la loro differenza sarà un angolo nullo.
È possibile trovare il doppio di un angolo? O il triplo? Certo! Possiamo trovare tutti i multipli di un angolo: basta sommare a quell’angolo un altro uguale o due uguali! Otteniamo i multipli di un angolo addizionando ad un angolo la sua stessa ampiezza un numero fissato di volte. Ma esistono anche i sottomultipli di un angolo: si ottengono suddividendo l’angolo in angoli congruenti. In che modo? Per esempio con la bisettrice di un angolo: è quella semiretta che divide l’angolo in due parti congruenti, cioè esattamente a metà. Ciascuna di queste due parti, quindi è un sottomultiplo dell’angolo di partenza.






