Solidi e solidi di rotazione: come affrontare i problemi

Un solido è una figura geometrica che possiede lunghezza, larghezza e altezza, e rappresenta la massima espressione di ciò che è tridimensionale. Sono figure che esistono nello spazio, che lo occupano in modo sostanziale.

Nel corso di questo articolo, faremo luce su che cosa sono i solidi, su come possono essere classificati e su come possono essere compresi e studiati. Esistono diverse tipologie di solidi, e nel corso dell’articolo ne esploreremo le varie categorie, dalle più semplici e intuitive a quelle più complesse e astratte. Ogni tipologia ha le sue peculiarità, le sue regole, una sua identità precisa, definita da specifiche proprietà geometriche e matematiche.

Affronteremo tutti i solidi più complessi, così da poter imparare come calcolarne la superficie e il volume anche se si tratta di figure più complesse di quelle a cui siamo abituati!

• Cosa sono i solidi composti
• Cosa sono i solidi bucati
• Quali sono i solidi di rotazione particolari
• Rotazione di un trapezio
• Strani solidi di rotazione
• Cosa sono i solidi misti

Cosa sono i solidi composti

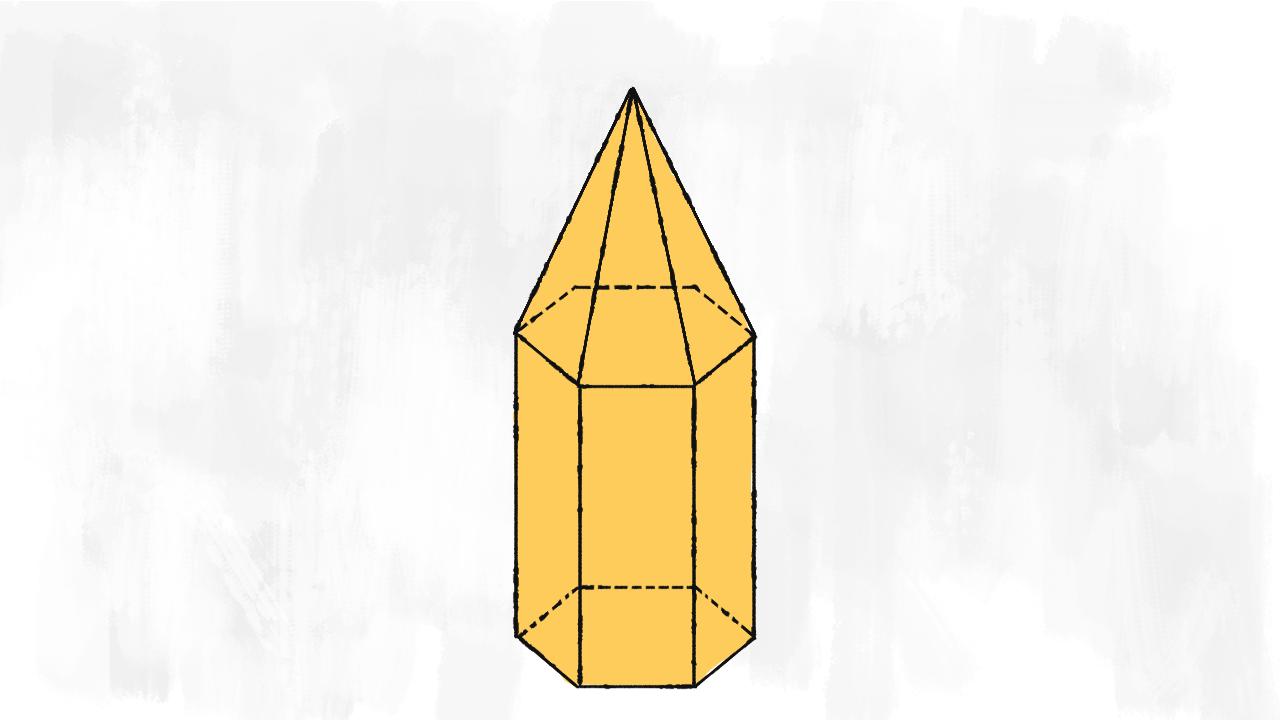
Ci sono problemi difficili con dei solidi più complessi. Cosa succede alla superficie e al volume di un solido formato da due parallelepipedi sovrapposti? O formato da un parallelepipedo sormontato da una piramide?

Per il volume non ci sono problemi: basta sommare il volume dei due solidi! Lo spazio occupato da questo solido composto è uguale alla somma degli spazi occupati dai due solidi singoli. Immaginiamo di riempire un contenitore della forma del solido in figura: la sua capacità totale è uguale alla somma delle capacità dei singoli solidi! Nel nostro caso, quindi, il volume totale è uguale alla somma del volume del prisma esagonale e del volume della piramide esagonale:

$$ V_{\text{solido}} = V_{\text{prisma}} + V_{\text{piramide}} $$

Cosa succede invece alla superficie? Se i due solidi sono sovrapposti su una delle due basi, come nel nostro caso, dobbiamo fare attenzione! La superficie totale del solido ottenuto non è uguale alla somma delle due superfici totali, ma dobbiamo escludere la base che hanno in comune. Immaginiamo di dover dipingere tutte le pareti del solido! La superficie totale è data dalla somma delle due superfici laterali più l’area di base del prisma:

$$ S_{\text{solido}} = S_{\ell\text{ prisma}} + S_{\ell\text{ piramide}} + A_{b\text{ prisma}} $$

Questo è solo un esempio! Fai attenzione a tutte le parti che si sovrappongono per poter calcolare correttamente la superficie del solido composto!

Cosa sono i solidi bucati

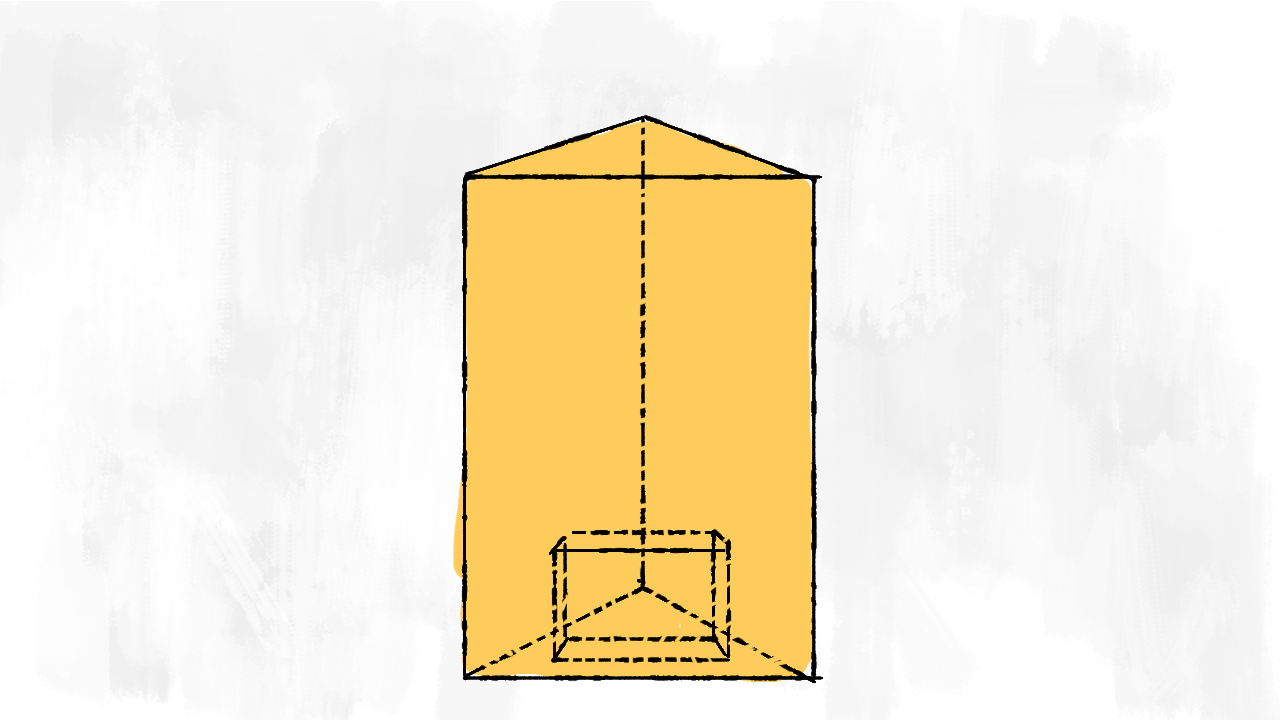
Qual è il volume di un prisma bucato? E sei il buco è a forma di piramide?

Dobbiamo sottrarre il volume del buco al volume del prisma. Prima di tutto dobbiamo individuare la forma del solido buco, poi, una volta calcolato il volume di entrambi i solidi, con una sottrazione riusciamo a trovare il volume totale del solido. Nel nostro esempio abbiamo un prisma triangolare bucato da un prisma rettangolare. Calcoliamo i due volumi! Il volume del solido finale è uguale alla differenza tra i volumi dei due solidi:

$$ V_{\text{solido}} = V_{\text{prisma triangolare}} – V_{\text{prisma rettangolare}} $$

Cosa succede invece per la superficie totale? Non è certo uguale alla differenza tra le superfici totali dei due solidi. E non è nemmeno uguale alla superficie totale del solido più grande. Basta contare le facce! Dobbiamo sommare le aree di tutte le facce del solido finale che abbiamo davanti. Nel nostro caso, quindi, dovremo sommare alla superficie totale del prisma triangolare, anche quattro facce del cubo, cioè la sua superficie laterale:

$$ S_{\text{solido}} = S_{tot\text{ prisma triangolare}} + S_{\ell\text{ prisma rettangolare}} $$

Quali sono i solidi di rotazione particolari

Rotazione di un triangolo ottusangolo

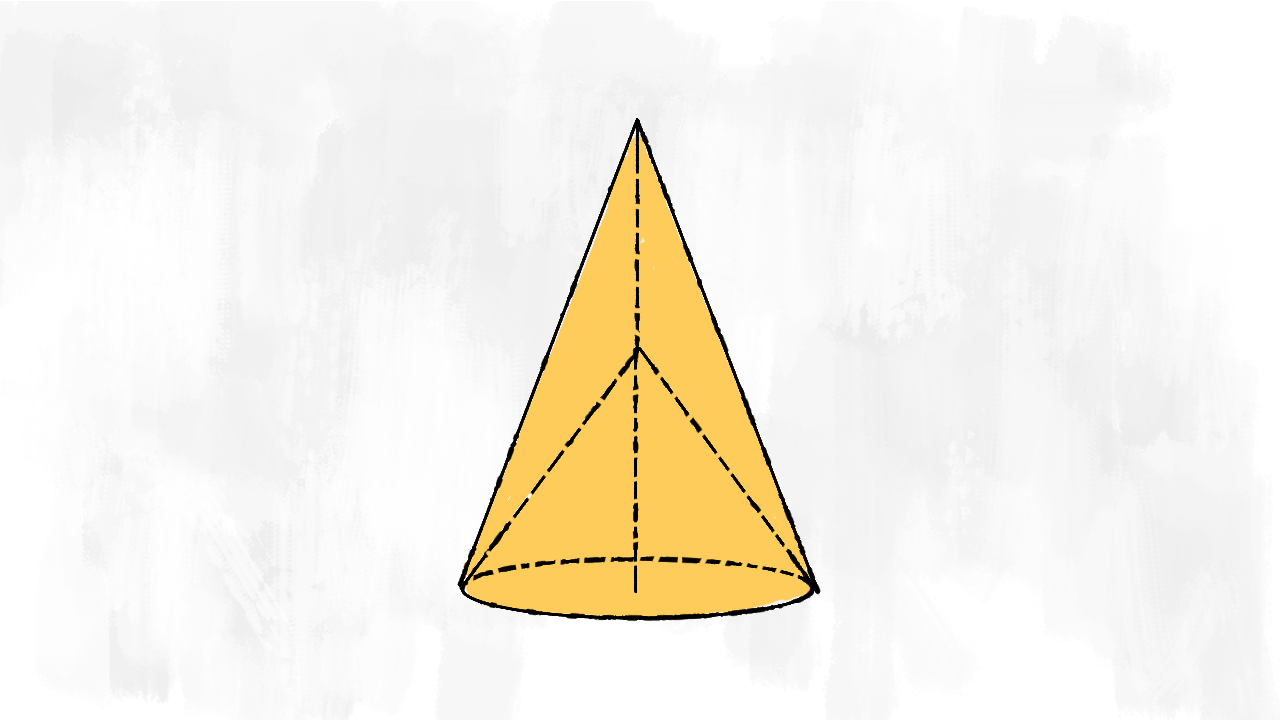
Rotazione di un triangolo acutangolo

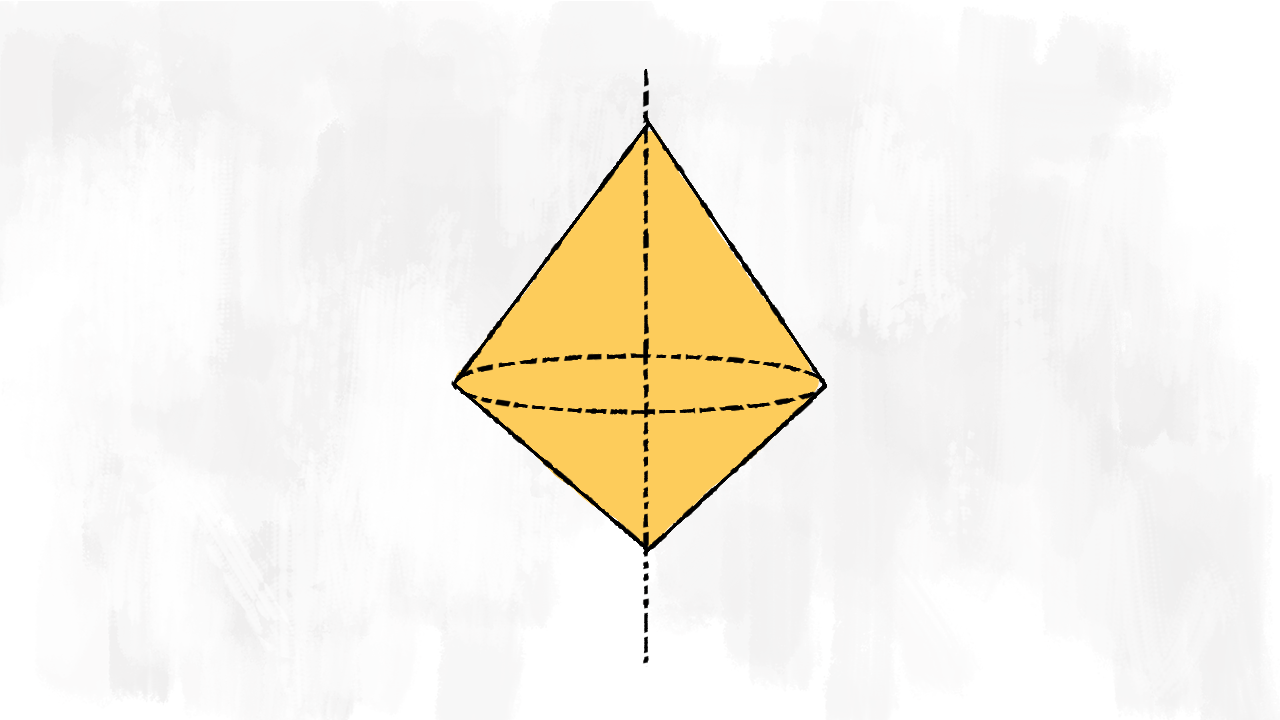
Proviamo a far ruotare un triangolo ottusangolo con asse su uno dei lati corti. Riesci a vedere che solido otteniamo?

È un cono a cui togliamo un cono più piccolo. Per calcolare il volume, quindi, non abbiamo problemi:

$$V_{\text{solido}}=V_{\text{cono grande}}-V_{\text{cono piccolo}}$$

I due coni hanno la stessa base!

Ma da cosa è formata la superficie totale? Immaginiamo di dipingere il solido: allora dipingiamo soltanto la superficie laterale del cono grande e quella del cono piccolo. Attenzione! Non dipingiamo la superficie di base! Sommiamo le due superfici laterali:

$$S_{\text{solido}}=S_{\ell\text{ cono grande}}+S_{\ell\text{ cono piccolo}}$$

Il secondo solido è composto da due parti: un cono grande e un cono piccolo, che formano le due punte. Anche in questo caso non abbiamo problemi per il volume, basta sommare:

$$V_{\text{solido}}=V_{\text{cono grande}}+V_{\text{cono piccolo}}$$

I due coni hanno la stessa base!

Ma da cosa è formata la superficie totale? Immaginiamo anche questa volta di dipingere il solido: come prima, dipingiamo soltanto la superficie laterale del cono grande e quella del cono piccolo. Attenzione! Non dipingiamo la superficie di base! Quindi ci basta sommare le due superfici laterali:

$$S_{\text{solido}}=S_{\ell\text{ cono grande}}+S_{\ell\text{ cono piccolo}}$$

Rotazione di un trapezio

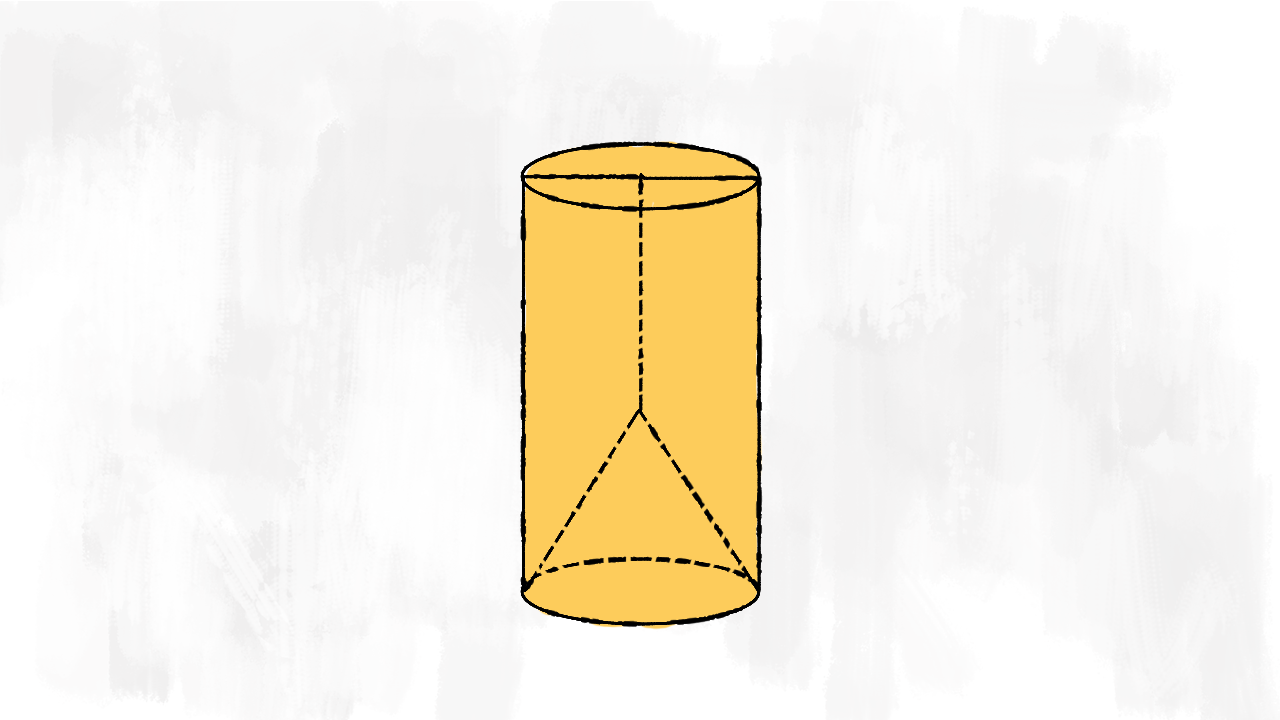
Rotazione trapezio rettangolo sulla base minore

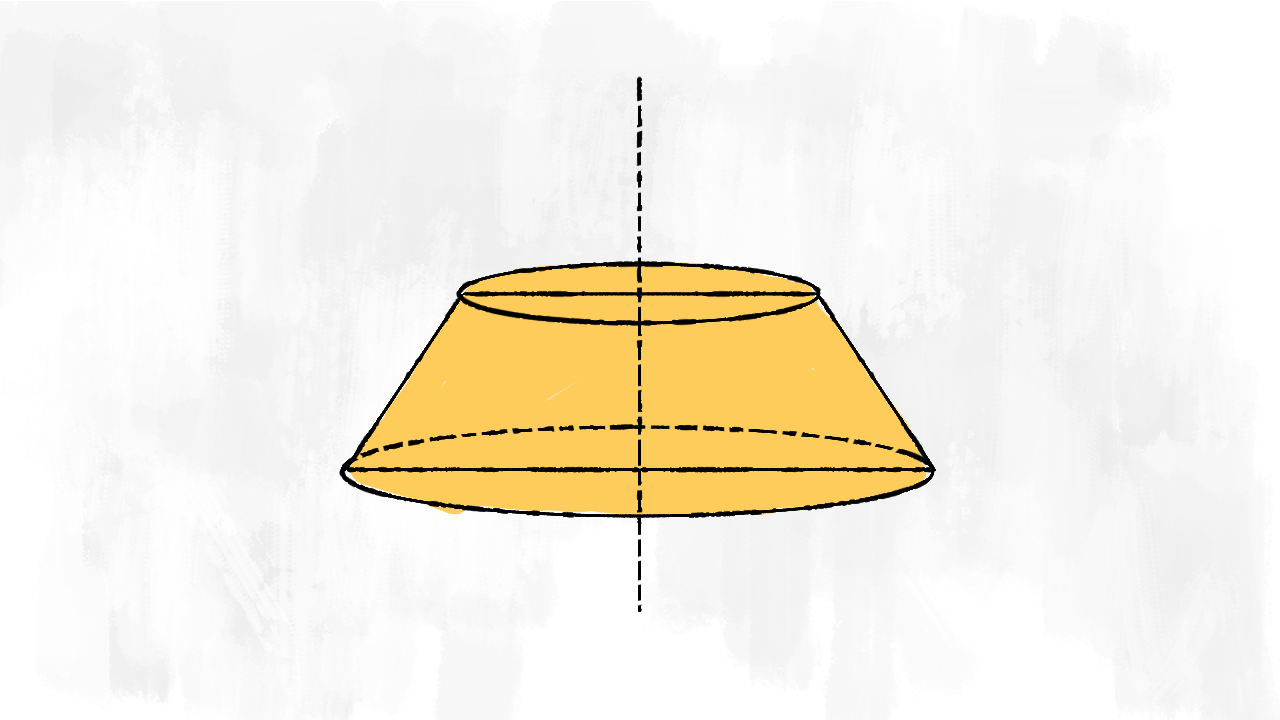
Rotazione trapezio scaleno sulla base maggiore

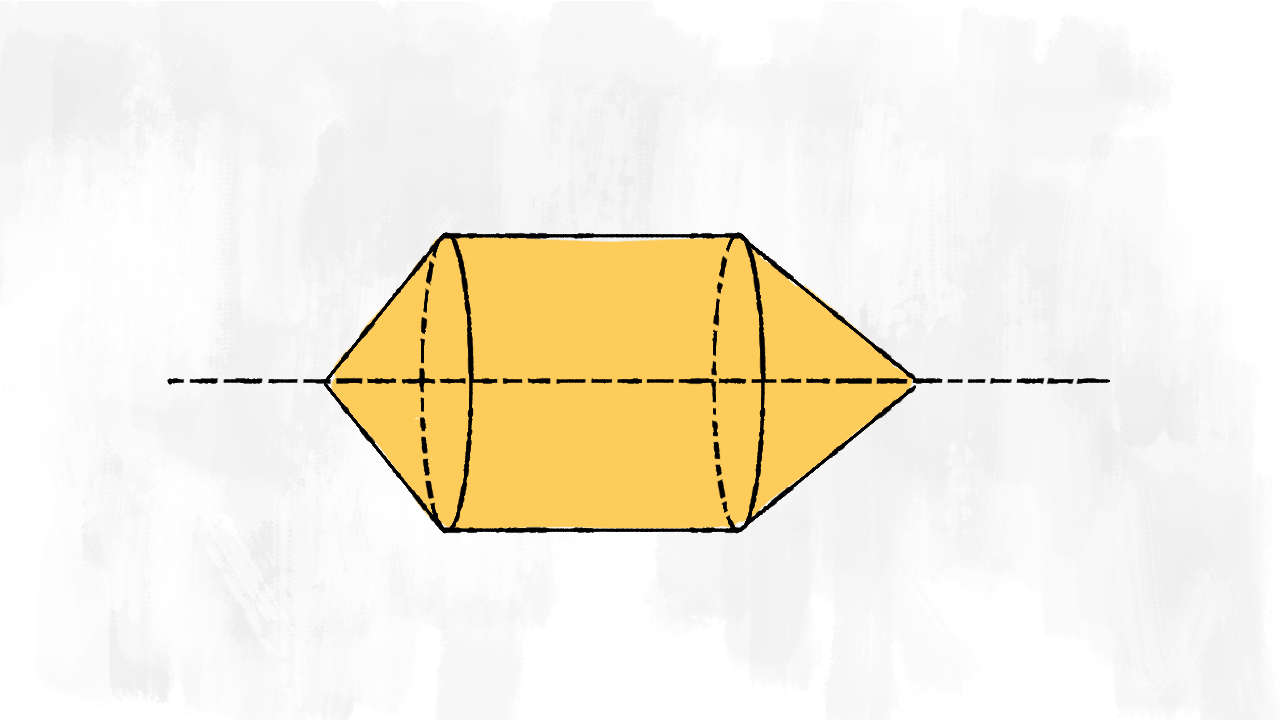
Rotazione trapezio rettangolo sull’altezza

Facendo ruotare un trapezio rettangolo sulla sua base minore, otteniamo un solido cavo: è un cilindro a cui togliamo un cono. Il volume è dato dalla differenza tra i due volumi:

$$V_{\text{solido}}=V_{\text{cilindro}}-V_{\text{cono}}$$

Osserva bene: i due solidi hanno la stessa base! Per vedere come è composta la superficie del solido, immaginiamo ancora di dipingerlo, coloriamo:

• la superficie laterale del cilindro
• la superficie laterale del cono
• l’area di una delle due basi del cilindro. Attenzione! Dipingiamo solo una delle due basi!

Sommiamo le due superfici laterali e una superficie di base per trovare la superficie totale di questo solido:

$$S_{\text{solido}}=S_{\ell\text{ cilindro}}+S_{\ell\text{ cono}}+A_{b\text{ cilindro}}$$

Il secondo solido è composto da tre parti: un cono grande e un cono piccolo, che formano le due punte, e un cilindro che forma la parte centrale. Per trovare il volume, ci basta sommare i volumi dei tre solidi:

$$V_{\text{solido}}=V_{\text{cono grande}}+V_{\text{cono piccolo}}+ V_{\text{cilindro}}$$

I due coni e il cilindro hanno la stessa base! Ma da cosa è formata la superficie totale? Immaginiamo anche questa volta di dipingere il solido: allora dipingiamo:

• la superficie laterale del cono grande
• la superficie laterale del cono piccolo
• la superficie laterale del cilindro. Attenzione! Non dipingiamo le superfici di base!

Sommiamo le tre superfici laterali per trovare la superficie totale del solido:

$$S_{\text{solido}}=S_{\ell\text{ cono grande}}+S_{\ell\text{ cono piccolo}}+S_{\ell\text{ cilindro}}$$

Il terzo solido possiamo immaginarlo così: un cono grande a cui tagliamo la punta. La punta non è altro che un cono più piccolo! Quindi, per trovare il volume del solido, facciamo la differenza tra i due volumi:

$$V_{\text{solido}}=V_{\text{cono grande}}-V_{\text{cono piccolo}}$$

Questo tipo di solido è un tronco di cono! C’è anche una formula per calcolare il volume di un solido fatto in questo modo! Chiamiamo £$ R $£ il raggio di base del cono grande, £$ r $£ il raggio di base del cono piccolo, £$ h $£ l’altezza del trapezio scaleno di partenza (che coincide poi con l’altezza del solido):

$$ V_{\text{tronco di cono}} = \frac 13 \pi h \cdot (R^2 + R\cdot r + r^2) $$

Questa volta i due solidi hanno basi diverse! Per capire com’è fatta la superficie totale immaginiamo sempre di dipingere il solido. Coloriamo:

• l’area di base del cono grande
• l’area di base del cono piccolo
• una parte della superficie laterale del cono grande. Attenzione! La parte di superficie laterale del cono grande è proprio la superficie laterale del cono grande a cui togliamo quella del cono piccolo!

Sommiamo le tre partie troviamo la superficie totale del solido:

$$S_{\text{solido}}=A_{b\text{ cono grande}}+A_{b\text{ cono piccolo}}+(S_{\ell\text{ cono grande}}-S_{\ell\text{ cono piccolo}})$$

Strani solidi di rotazione

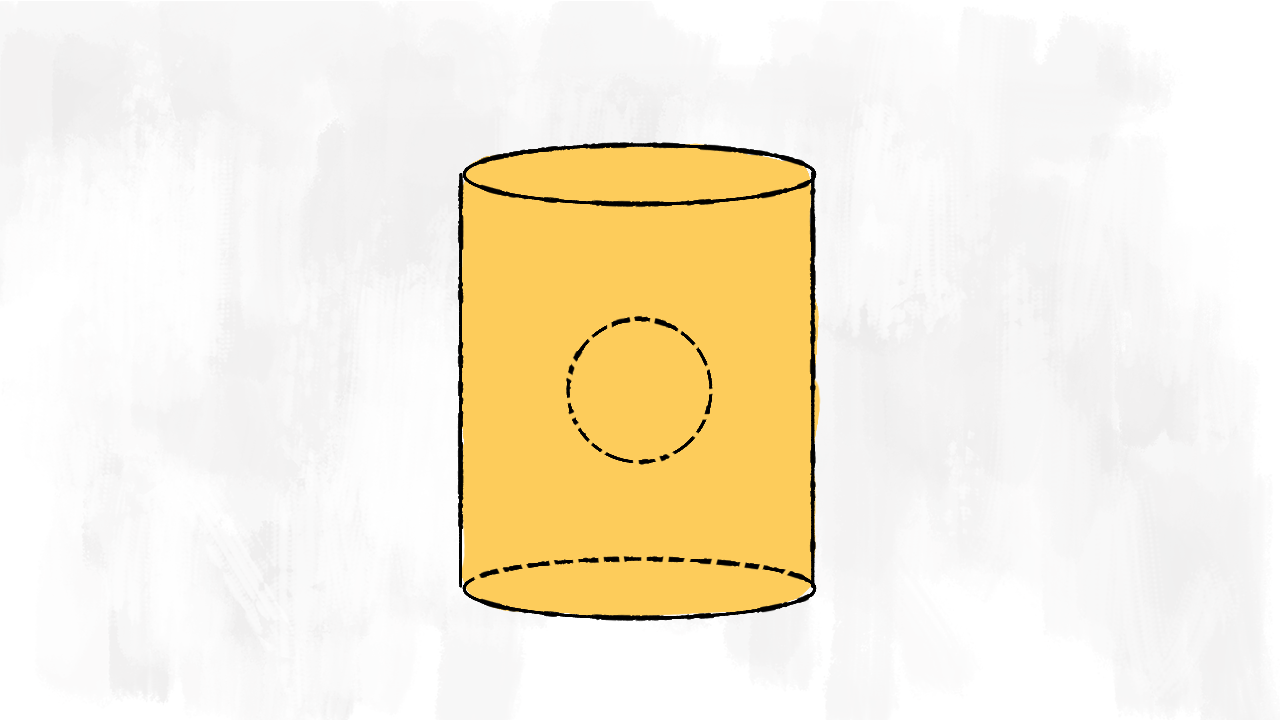
Cilindro con un buco a forma di sfera

Cilindro bucato

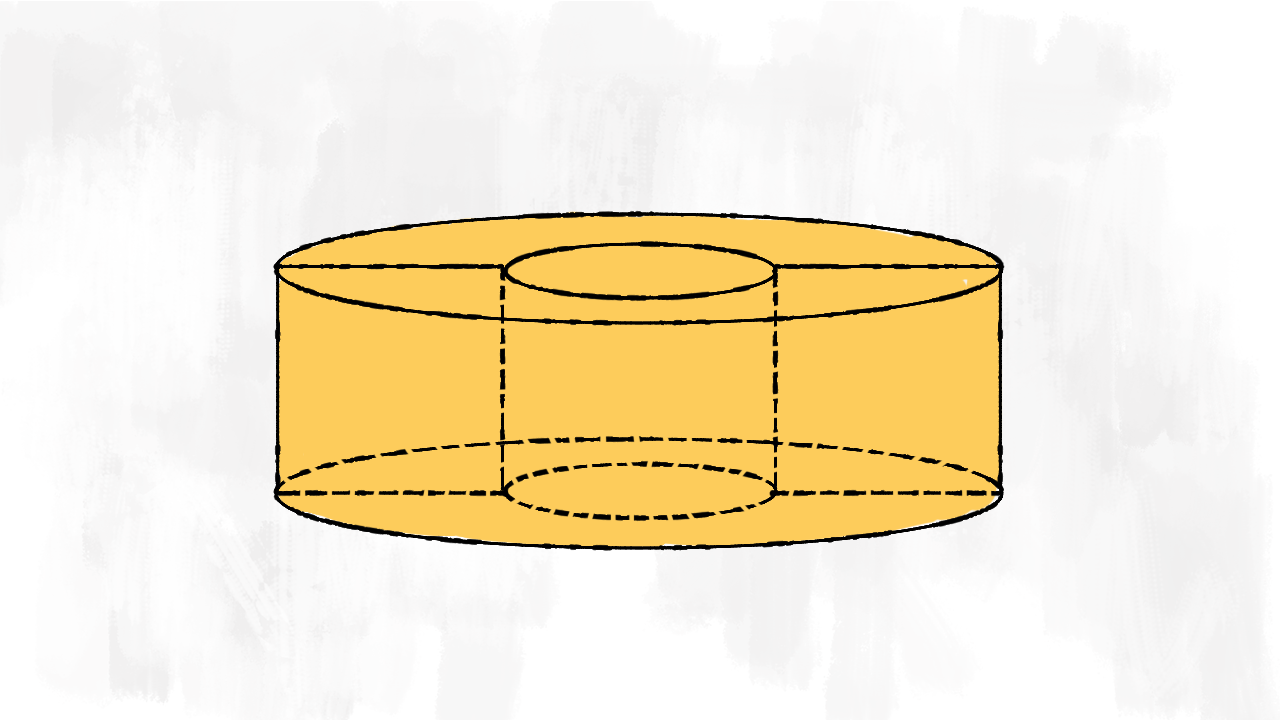
Il primo solido è un po’ strano… Ha un buco interno a forma di sfera: è un cilindro a cui togliamo una sfera. Il volume è uguale alla differenza tra i due volumi:

$$V_{\text{solido}}=V_{\text{cilindro}}-V_{\text{sfera}}$$

La superficie del solido è formata dalla superficie totale del cilindro (parte esterna) e da quella della sfera (parte interna)! Anche se non la vediamo, dobbiamo considerarla come superficie esterna del solido! Sommiamo le due superfici:

$$S_{\text{solido}}=S_{tot\text{ cilindro}}+S_{\text{sfera}}$$

Il secondo solido possiamo immaginarlo così: un cilindro bucato, che ha per base una corona circolare!

$$V_{\text{solido}}=V_{\text{cilindro grande}}-V_{\text{cilindro piccolo}}$$

Per capire com’è fatta la superficie totale immaginiamo sempre di dipingere il solido. Coloriamo:

• la superficie laterale del cilindro grande (parte esterna)
• la superficie di base del cilindro piccolo (parte interna)
• una parte delle superfici di base del cilindro grande. Attenzione! La parte di superficie di base del cilindro grande è proprio la superficie di base del cilindro grande grande a cui togliamo quella del cilindro piccolo. E non dimenticare che le basi sono due!

Sommiamo le tre parti per trovare la superficie totale del solido:

$$S_{\text{solido}}=S_{\ell\text{ cilindro grande}}+S_{\ell\text{ cilindro piccolo}}+2\cdot(A_{b\text{ cilindro grande}}-A_{b\text{ cilindro piccolo}})$$

Cosa sono i solidi misti

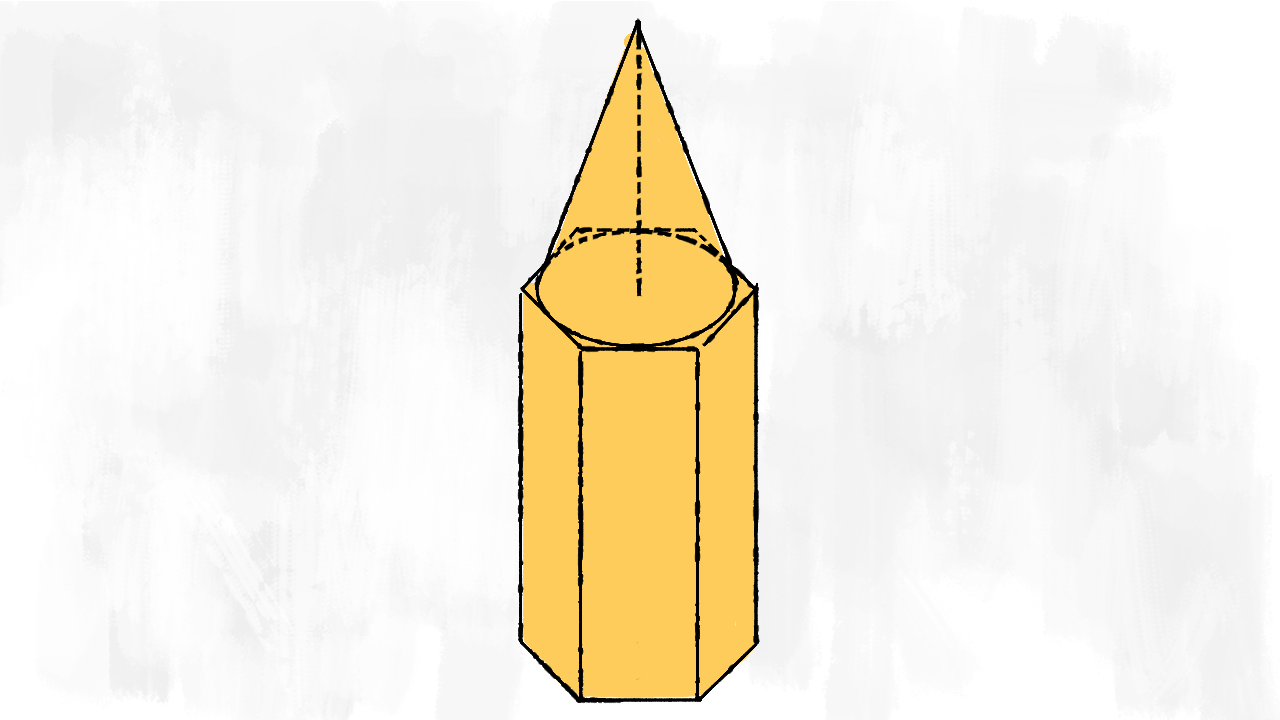
Prisma sormontato da un cono

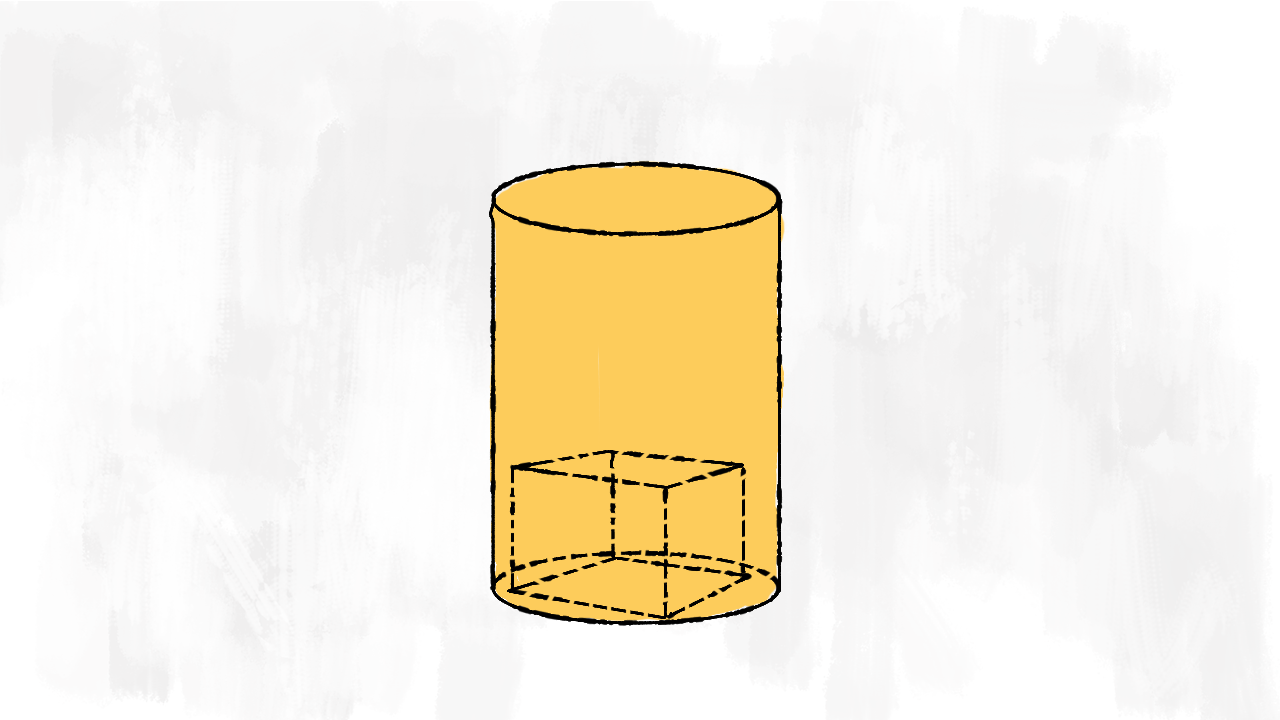
Cilindro bucato da un cubo

Come ci dobbiamo comportare se troviamo un cono sopra ad un prisma? Oppure un cilindro bucato da un altro solido? Per il volume possiao fare riferimento agli altri esempi che abbiamo già visto per i solidi composti o i solidi bucati. Come facciamo invece a trovare la superficie totale di questi solidi?

La prima immagine rappresenta un prisma regolare con sovrapposto un cono la cui base è inscritta nella base del prisma. Immaginiamo di dover dipingere questo solido: che cosa dobbiamo colorare?

• l’area di base del prisma
• la superficie laterale di prisma
• la superficie laterale del cono

Però avanza anche un pezzetto! Questa volta, infatti, le basi dei due solidi non sono uguali, quindi dobbiamo dipingere anche la differenza tra le due basi (che nell’immagine è evidenziata in… ). Per trovare la superficie totale del solido, quindi, sommiamo tutti i pezzi:

$$ S_{\text{solido}} = S_{\text{tot prisma}} + S_{\ell \text{ cono}} – A_{b \text{ cono}} $$

Prova a capire quale sarebbe invece la superficie totale dello stesso prisma, ma con un buco a forma di cono! Il risultato è molto simile a quello che abbiamo appena trovato. 😉

Nel secondo esempio, invece, vediamo un solido formato da un cilindro bucato con un cubo la cui base è all’interno della base del cilindro. Come facciamo a trovare il volume? Si tratta di un solido bucato, quindi dobbiamo fare semplicemente la differenza tra i due volumi. E per calcolare la superficie totale, invece? Vediamo quali parti dobbiamo dipingere per colorare tutto il solido:

• l’area di base del cilindro
• la superficie laterale del cilindro
• la superficie laterale del cubo

Osserviamo però la base che i due solidi hanno in comune: non sono congruenti! Quindi dobbiamo dipingere anche quel pezzettino che è equivalente alla differenza tra le due aree di base. In conclusione, la superficie totale del solido è:

$$ S_{\text{solido}} = S_{\text{tot cilindro}} + S_{\ell \text{ cubo}} $$