Figure coniche: eccentricità e direttrici
L’eccentricità e le direttrici sono concetti chiave nell’ambito delle coniche, figure geometriche che emergono dall’intersezione di un cono con un piano.
Questi concetti non solo offrono una profonda comprensione delle proprietà geometriche e delle relazioni tra diverse coniche, come ellissi, parabole e iperboli, ma aprono anche la porta a un’ampia gamma di applicazioni in fisica, astronomia, ingegneria e oltre.
In questa lezione vedrai come riconoscere una conica dal valore dell’eccentricità, cioè dal valore del rapporto tra la distanza dal fuoco e la distanza tra la direttrice. Scoprirai anche che l’ellisse e l’iperbole hanno due direttrici!
- Definizione di conica
- Che cos'è l'eccentricità
- Direttrici di ellisse e iperbole
- Cosa potrebbero chiederti nell'interrogazione sulle coniche
- Sfida sull'eccentricità
Definizione di conica
Una conica è una figura geometrica ottenuta come intersezione di un piano con un cono doppio infinito. La natura specifica della conica – che può essere un’ellisse, una parabola o un’iperbole – dipende dall’angolazione del piano rispetto all’asse del cono.
- Se il piano taglia il cono in modo parallelo all’asse, otteniamo una parabola.
- Se l’angolazione è tale che il piano interseca entrambe le nappe del cono ma non è parallelo all’asse, la figura risultante è un’iperbole.
- Se il piano taglia il cono in un angolo meno inclinato rispetto all’asse, senza attraversare la base, emerge un’ellisse.
Questa definizione geometrica fornisce una base per esplorare le notevoli proprietà delle coniche, inclusa la loro rappresentazione algebrica attraverso equazioni di secondo grado, la loro simmetria, e le loro applicazioni pratiche in vari campi scientifici e tecnologici.
Che cos’è l’eccentricità
Una conica è il luogo geometrico dei punti £$P$£ del piano per i quali è costante il rapporto tra la distanza dal fuoco e la distanza dalla direttrice. Chiamiamo questo rapporto £$e$£ (eccentricità) e lo usiamo per caratterizzare la conica:
- £$e=0$£ circonferenza;
- [iol_placeholder type="formula" engine="katex" display="inline"]0
- £$e=1$£ parabola;
- £$e > 1 $£ iperbole.
Direttrici di ellisse e iperbole
Quando abbiamo studiato l’ellisse e l’iperbole, abbiamo visto che i fuochi giocano un ruolo importante nella loro definizione. Ora ci aspettiamo che queste due curve abbiano anche due direttrici. Ma quali sono le equazione delle direttrici?
Per l’ellisse e l’iperbole con i fuochi sull’asse £$x$£ abbiamo £$x=\pm\frac{a^2}{c}$£ mentre se i fuochi sono sull’asse £$y$£ otteniamo £$x=\pm\frac{b^2}{c}$£.
Cosa potrebbero chiederti nell’interrogazione sulle coniche
Testo degli esercizi:

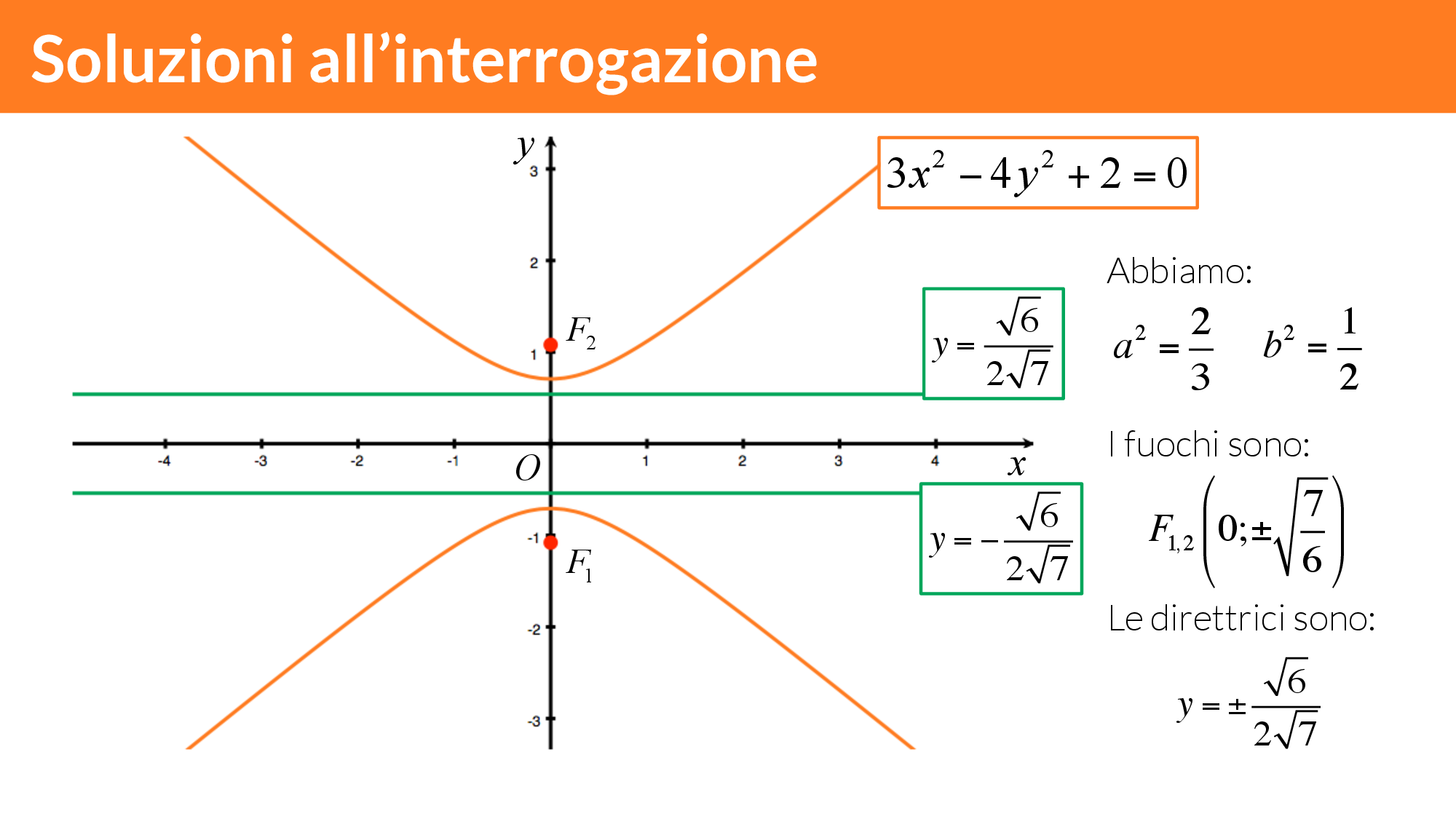
Soluzione degli esercizi:
Metti alla prova la tua preparazione sulle coniche: sai che cos’è e cosa significa il valore dell’eccentricità? Sai trovare le direttrici di una conica? Prova a rispondere a queste e a altre domande che trovi qui sopra!
Sfida sull’eccentricità
Sfida:
Soluzione:
Dopo aver tracciato l’itinerario sulla cartina di Roma ti accorgi che, ruotandola opportunamente, tutti i punti del percorso hanno distanza dalla stazione Termini pari al doppio della distanza che li separa dalla retta che congiunge il Vaticano con il Colle Aventino. Che tipo di percorso hai disegnato sulla cartina?