Il campo elettrico: qual è la sua definizione

Il campo elettrico è uno dei pilastri su cui si fonda la fisica moderna, un’entità invisibile che occupa lo spazio intorno alle cariche elettriche, esercitando forze su altre cariche presenti in quel campo. È un concetto chiave per comprendere non solo teorie fisiche più avanzate, ma anche per applicazioni pratiche quotidiane, come il funzionamento degli elettrodomestici o la trasmissione dei segnali di comunicazione.

La generazione di un campo elettrico avviene attorno a cariche elettriche, sia che queste siano fisse sia che siano in movimento. La sua intensità e direzione possono essere determinate osservando l’effetto che il campo ha su una carica di prova collocata al suo interno.

Cerchiamo di definirlo meglio e di capire quali sono gli elementi più importanti!

• Definizione del campo elettrico
• Le linee di forza del campo elettrico
• Il flusso del campo elettrico statico e la legge di Gauss
• La circuitazione del campo elettrico

Definizione del campo elettrico

Una carica elettrica £$Q$£ posta all’interno di uno spazio (anche vuoto), è in grado di modificarlo. Come? Producendo un campo elettrostatico (con statico si intende prodotto da una carica ferma)!

Tale campo, presente indipendentemente da altri oggetti carichi posti nelle sue vicinanze, è in grado di modificare lo spazio in cui la carica viene inserita (esattamente come accadeva per il [postLink:6464]) e generare una perturbazione elettrica che si propaga alla velocità della luce (£$300 \ 000 \frac{km}{s}$£); inoltre, pur non interagendo coi corpi neutri, ha la capacità di agire su altre cariche che si trovano nei pressi della carica generatrice.

Per studiare la sua struttura è necessario utilizzare una carica di prova, o esploratrice, £$q$£ con le seguenti caratteristiche:

• deve essere puntiforme, cioè di dimensioni trascurabili;
• per convenzione positiva;
• con carica trascurabile, al fine di non modificare le caratteristiche del campo elettrico che si vuole analizzare;

Il modulo del vettore campo elettrico può essere dunque calcolato come rapporto tra £$F$£ e £$q$£, carica di prova: £$E = \frac{F}{q} \left( \frac{N}{C} \right)$£.

La direzione della forza è quella della retta che congiunge la carica esploratrice e la carica generatrice e il verso dipende dal segno di £$Q$£: è uscente se la carica £$Q$£ è positiva ed entrante se £$Q$£ è negativa.

L’esempio più semplice di campo elettrico è quello prodotto da una carica positiva e puntiforme £$Q$£.

Se ponessimo in prossimità di £$Q$£ una carica di prova £$q$£, essa risentirebbe dell’azione di una forza pari a:

£$F_c = k \frac {|Q| \cdot |q|}{r^2}$£ (forza elettrica di Coulomb)

Applicando la definizione di campo elettrico possiamo così trovare l’intensità di £$E$£:

£$E = \frac{F}{q} = \frac{k \frac {|Q| \cdot |q|}{r^2}}{q} = k \frac {Q}{r^2}$£

Come è possibile notare dalla formula, il campo elettrico dipende unicamente dalla carica £$Q$£ che lo genera!

Le linee di forza del campo elettrico

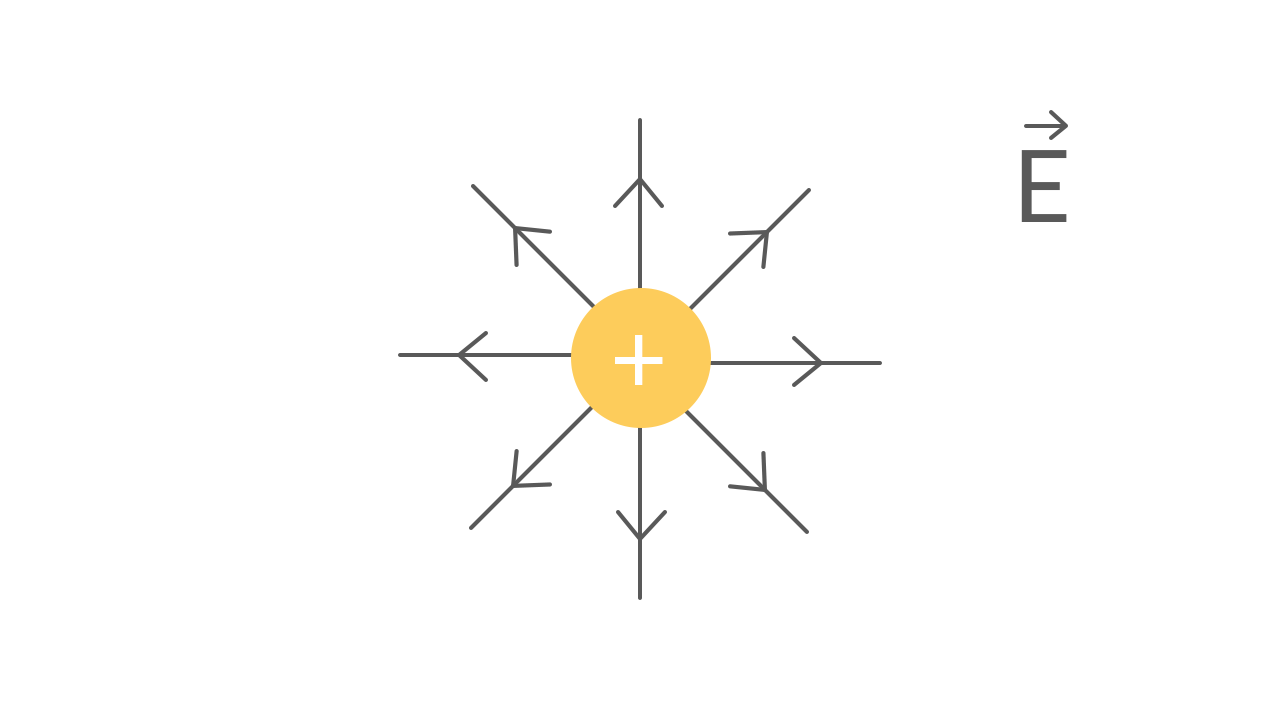
Non è semplice pensare al concetto di “campo", trattandosi di un fenomeno di cui si vedono solo gli effetti, non visibile o tangibile. Nonostante ciò, nel corso degli anni, sono stati introdotti metodi utili per rappresentarlo nel piano e nello spazio. Essi permettono di raffigurare il campo elettrico come un insieme di linee, chiamate linee di forza del campo, aventi delle caratteristiche molto particolari:

• sono le traiettorie che seguirebbe una carica di prova positiva posta nel campo;
• in ogni punto il vettore campo elettrico è tangente alle linee di forza;
• il numero delle linee di forza dipende dall’intensità del campo elettrico.

Per fare un esempio, consideriamo la figura riportata all’inizio del post: il campo elettrico è generato da una carica puntiforme positiva, le linee di forza sono radiali ed escono dalla carica, le linee di forza sono più “fitte" in prossimità della carica.

Il flusso del campo elettrico statico e la legge di Gauss

Esattamente come accade per qualsiasi altro campo vettoriale, anche per il campo elettrico è possibile definire il flusso. Il primo ad introdurre il concetto di flusso, nell’ambito della fluidodinamica, (ripassa tutti i concetti della dinamica dei fluidi con le nostre lezioni!) fu Johann Carl Friedrich Gauss, un fisico e matematico tedesco che operò tra il XVIII e il XIX secolo.

Gauss definì il flusso di un campo vettoriale come prodotto scalare tra il vettore superficie £$\vec A$£ e il vettore campo £$\vec C$£ (dove £$C$£ indica qualsiasi tipo di campo vettoriale) :

£$\Phi = \vec A \cdot \vec C = A \cdot C \cdot cos \alpha$£

Dove £$\vec A$£ è uno strumento matematico, il vettore superficie, introdotto per ottenere uno scalare da un prodotto tra vettori. L’unità di misura del flusso del campo elettrico nel SI è £$N \frac{m^2}{C}$£. Il vettore superficie ha per modulo l’area della superficie, la direzione è perpendicolare alla superficie, il verso è quello uscente dalla superficie.

Se il campo attraversa una superficie chiusa, il flusso è positivo per le linee che escono dal volume racchiuso dalla superficie e negativo per le linee che entrano nel volume racchiuso dalla superficie.

Il flusso di un campo è uno strumento matematico che non è trasponibile alla realtà, ma può essere immaginato come un fascio di vettori campo che attraversano una superficie!

Un risultato particolarmente interessante a cui pervenne Gauss fu che il flusso attraverso una superficie chiusa qualsiasi era calcolabile come rapporto tra la carica totale £$q$£ contenuta nella superficie e la costante dielettrica £$\epsilon_m$£ del materiale considerato:

£$\Phi = \frac{q}{\epsilon_m}$£

ATTENZIONE! Con £$\epsilon_m$£ si intende la costante dielettrica del materiale ottenuta come prodotto tra la costante dielettrica del vuoto £$\epsilon_0$£ e quella relativa del materiale £$\epsilon_r$£.

La circuitazione del campo elettrico

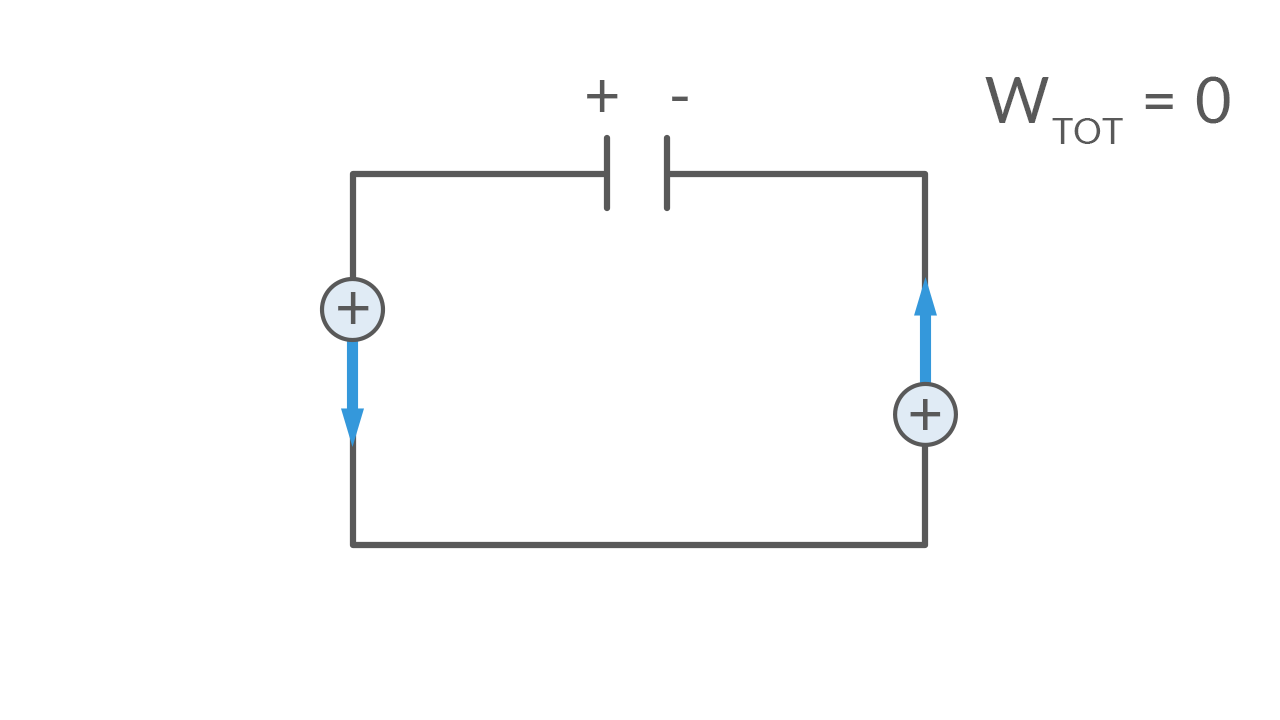
La circuitazione di un campo vettoriale è una grandezza scalare derivata indicata solitamente con £$\Gamma$£ che definisce il lavoro fatto dalla forza generata da un campo lungo un percorso chiuso. Dato che una forza si definisce conservativa se il lavoro totale che compie non dipende dal percorso ma solo dal punto di partenza ed arrivo, se tale forza è generata da un campo, anche quest’ultimo sarà conservativo.

In sostanza la circuitazione aiuta a distinguere campi conservativi da campi non conservativi tramite le forze che generano.

La circuitazione di un campo vettoriale generico £$\vec V$£si può calcolare come l’integrale di linea lungo £$l$£ del campo £$ \vec V $£: £$\Gamma (\vec V)= \oint V \ dl$£.

Nel caso del campo elettrico la sua circuitazione diventa £$\Gamma (\vec E)$£= £$\oint E \ dl$£. La circuitazione di un campo elettrostatico è nulla, poiché il campo elettrico e la forza elettrica sono conservativi, cioè il lavoro totale fatto dalla forza elettrica per portare una carica da un punto A ad un punto B dipende solo dalla posizione iniziale e finale, inoltre, se le posizioni coincidono, il lavoro è nullo. Abbiamo definito tramite la circuitazione che il campo elettrico statico è conservativo.