La legge della gravitazione universale di Isaac Newton

La legge di gravitazione universale è uno dei pilastri fondamentali sulla cui base si basa la nostra comprensione dell’universo. È una legge che riguarda ogni singolo corpo celeste, ogni stella, pianeta, e perfino ogni oggetto sulla Terra, spiegando la forza invisibile che tiene tutto insieme. Mentre oggi prendiamo come scontata la nostra comprensione della gravità e del suo ruolo nell’universo, vi fu un tempo in cui l’idea di una forza invisibile che potesse agire attraverso il vuoto dello spazio era rivoluzionaria.

Questa forza, che operava sia tra mele che cadevano dagli alberi sia tra pianeti lontani, è stata identificata e descritta per la prima volta da Isaac Newton nel XVII secolo. Il suo lavoro sull’argomento ha gettato le basi per secoli di ricerca e ha aperto la porta a una nuova era di comprensione del nostro posto nell’universo. In questo articolo, esploreremo la storia dietro la scoperta della legge di gravitazione universale, il suo impatto sulla scienza e come Isaac Newton è arrivato a formularla.

• La scoperta della gravitazione universale di Isaac Newton
• La legge di gravitazione universale
• L'accelerazione di gravità
• Cos'è un campo gravitazionale

La scoperta della gravitazione universale di Isaac Newton

La storia della scoperta della gravitazione universale da parte di Isaac Newton è tanto affascinante quanto il principio stesso. Si racconta che Newton fu ispirato a riflettere sulla gravità vedendo una mela cadere da un albero nel suo giardino a Woolsthorpe, anche se questa storia è probabilmente più leggenda che realtà.

Tuttavia, ciò che sappiamo con certezza è che Newton si immerse profondamente nei problemi della fisica del suo tempo. Durante il suo periodo all’Università di Cambridge, lesse i lavori di Galileo e Keplero, due figure chiave che avevano studiato il movimento dei corpi nel cielo. Attraverso meticolose osservazioni e intensi calcoli matematici, Newton iniziò a sviluppare le sue leggi del movimento.

Il vero genio di Newton emerse quando realizzò che la stessa forza responsabile della caduta di una mela verso il suolo era anche responsabile del movimento della Luna intorno alla Terra e dei pianeti intorno al Sole, ed è così che è giunto alla formulazione della sua teoria della gravitazione universale.

La legge afferma che ogni particella di materia nell’universo attrae ogni altra particella con una forza direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza tra i loro centri. Con questa legge, Newton non solo riuscì a spiegare i movimenti osservati dei corpi celesti, ma fornì anche un quadro unificato che collegava il mondo terrestre a quello celeste sotto una stessa forza fondamentale. Il suo “Philosophiæ Naturalis Principia Mathematica" del 1687, in cui presentò la sua teoria, rimane uno dei più grandi trattati scientifici mai scritti.

La legge di gravitazione universale

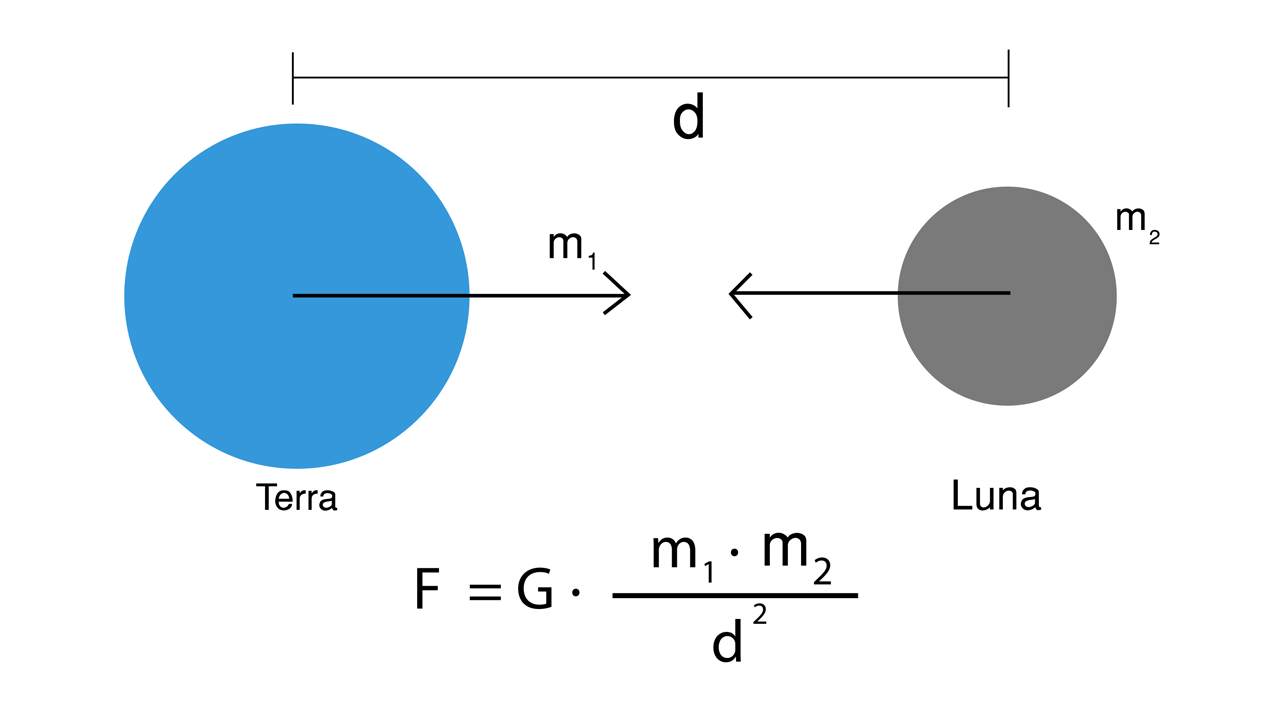
La legge di gravitazione universale:
nell’Universo due corpi si attirano in modo direttamente proporzionale alle loro masse e inversamente proporzionale alla loro distanza elevata al quadrato, lungo la retta che congiunge i due corpi.

$$F=G{\frac {m_{1}m_{2}}{d^{2}}} $$

in cui:

• £$F$£ è l’intensità della forza tra le masse;
• £$G$£ è la costante di gravitazione universale (£$6.67\cdot 10^{-11}\text{N}\cdot\text{m}^2\text{kg}^{-2}$£, determinata dai risultati dell’esperimento dello scienziato inglese Henry Cavendish condotto nel 1798);
• £$m_1$£ è la prima massa;
• £$m_2$£ è la seconda massa;
• £$d$£ è la distanza tra i centri delle masse.

Attenzione!
Se una delle masse raddoppia, la forza di gravitazione raddoppia; se anche l’altra massa raddoppia, la forza di gravitazione diventa 4 volte più grande.
Se la distanza raddoppia, la forza di gravitazione diventa 4 volte più piccola; se la distanza triplica, la forza di gravitazione diventa 9 volte più piccola.

L’accelerazione di gravità

L’accelerazione di gravità si indica con la lettera £$g$£ e la sua unità di misura è il metro al secondo quadrato £$ \left(\frac{\text{m}}{\text{s}^2} \right)$£.
Il simbolo è £$g$£ minuscolo per distinguerlo dalla costante gravitazionale £$G$£ che compare nell’equazione di Newton.

Il suo valore esatto sulla Terra varia a seconda del luogo, in particolare della latitudine e dell’altitudine: per questo motivo è stato introdotto un valore convenzionale per £$g$£, pari a £$9,80665 \frac{\text{m}}{\text{s}^2}$£.
È un valore medio che approssima il valore dell’accelerazione di gravità presente al livello del mare ad una latitudine di 45,5°. Tale valore viene a volte rappresentato con £$g_0$£, quando £$g$£ viene invece usato per rappresentare l’effettiva accelerazione di gravità locale.

Calcolo di £$g$£

A partire dalla legge della gravitazione universale, £$g$£ è il prodotto di alcuni termini che vi compaiono, cioè:

£$F=G\;{\frac {m_{1}\;m_{2}}{r^{2}}}=\left(G\;{\frac {m_{1}}{r^{2}}}\right)m_{2}$£

£$g=G{\frac {m_{1}}{r^{2}}}$£
Inserendo quindi i valori di G, della massa e del raggio della Terra si ottiene una buona approssimazione del valore medio di £$g$£:

$$g=G{\frac {m_{1}}{r^{2}}=\left(6{,}6742\cdot 10^{-11}\ \mathrm {Nm^{2}kg^{-2}} \right){\frac {5{,}9736 \cdot 10^{24}\ \mathrm {kg} }{\left(6{,}37101\cdot 10^{6}\ \mathrm {m} \right)^{2}}}=9{,}822\ \mathrm {\frac{m}{s^{2}}} }$$

Attenzione!
Le differenze sono dovute al fatto che la Terra non è omogenea, non è una sfera perfetta: viene considerato un valore medio del suo raggio ed il calcolo non tiene conto dell’effetto centrifugo dovuto alla rotazione del pianeta (forza centrifuga apparente che è massima all’equatore e nulla ai poli).

Cos’è un campo gravitazionale

Il campo gravitazionale è definito come la “deformazione dello spazio-tempo creata dalla presenza di corpi dotati di massa o energia".
In meccanica classica il campo gravitazionale è trattato come un campo di forze conservativo.

Il campo gravitazionale generato dalla Terra, ad esempio, in prossimità della superficie terrestre assume valori prossimi a £$9,8 \mathrm {\frac{m}{s^{2}}}$£ e per convenzione si adotta tale valore di riferimento per l’accelerazione di gravità.

Il campo generato nello spazio dalla presenza di una massa nel punto £$O$£, origine del riferimento, è definito come:

$$g(r) = -GM\frac{r}{r^3}$$

dove £$G$£ è la costante di gravitazione universale, £$M$£ la massa e £$ r $£ la distanza dall’origine del punto in cui si misura il valore del campo gravitazionale.

È quindi possibile esprimere la forza esercitata sul corpo di massa £$m$£ come:

$$F(r) = m \cdot g(r)$$

L’unità di misura del campo gravitazionale nel Sistema internazionale è:

$$[g] = \big[ \mathrm{\frac{N}{kg}} \big] = \big[ \mathrm{\frac{m}{s^2}} \big]$$

dove £$g = |g| $£ è il modulo di £$g$£.