Keplero e le sue tre leggi sul movimento dei pianeti
Questo astronomo e matematico tedesco, operante tra la fine del XVI e l’inizio del XVII secolo, non è solo una figura chiave nella rivoluzione scientifica, ma anche un pilastro nel ponte che ha collegato l’astronomia antica alla fisica moderna. Nella sua ricerca appassionata dei meccanismi celesti, Keplero ha svelato alcune delle leggi fondamentali che governano i movimenti dei corpi celesti, gettando le basi per la successiva comprensione gravitazionale di Isaac Newton.
Ma che cosa ha spinto Keplero nella sua indagine sugli astri? E come ha fatto a dedurre le sue famose leggi? Nato in un’epoca in cui l’astronomia era in tumultuoso cambiamento, con il sistema eliocentrico di Copernico che sfidava l’antica visione geocentrica, Keplero era determinato a trovare un’armonia matematica nell’universo lo ha portato a formulare le tre leggi del movimento planetario, che ancora oggi sono centrali nell’astronomia e nella fisica.
Scopriamo insieme le sue tre leggi!
Keplero e le sue tre leggi
Johannes Kepler (1571 – 1630) nacque in Germania e fu un grandissimo astronomo, astrologo, matematico e teologo evangelico. Grazie alle osservazioni dei moti e delle posizioni dei pianeti di Copernico e al lavoro di calcolo di Brahe, Keplero dedusse le omonime leggi che descrivono le orbite dei pianeti attorno al Sole, perfezionando il modello eliocentrico copernicano descritto per la prima volta in “Delle rivoluzioni dei corpi celesti" del 1543.
Fino al 1600 il sistema aristotelico-tolemaico, dato da un’unione dei lavori di astronomia antica di Aristotele e Tolomeo, descriveva un modello di universo geocentrico con la Terra al centro della sfera celelste attorno alla quale tutti i pianeti, le stelle e i satelliti come la Luna, erano in movimento secondo orbite circolari.
Niccolò Copernico (Nikolas Koppernigk 1473-1543, astronomo polacco) fu il primo a proporre un modello di universo eliocentrico, con il Sole al centro del nostro sistema e tutti gli oggetti in moto attorno ad esso secondo orbite circolari. Keplero riprese tale modello perfezionandolo e descrivendolo tramite le sue leggi.
Prima legge di Keplero
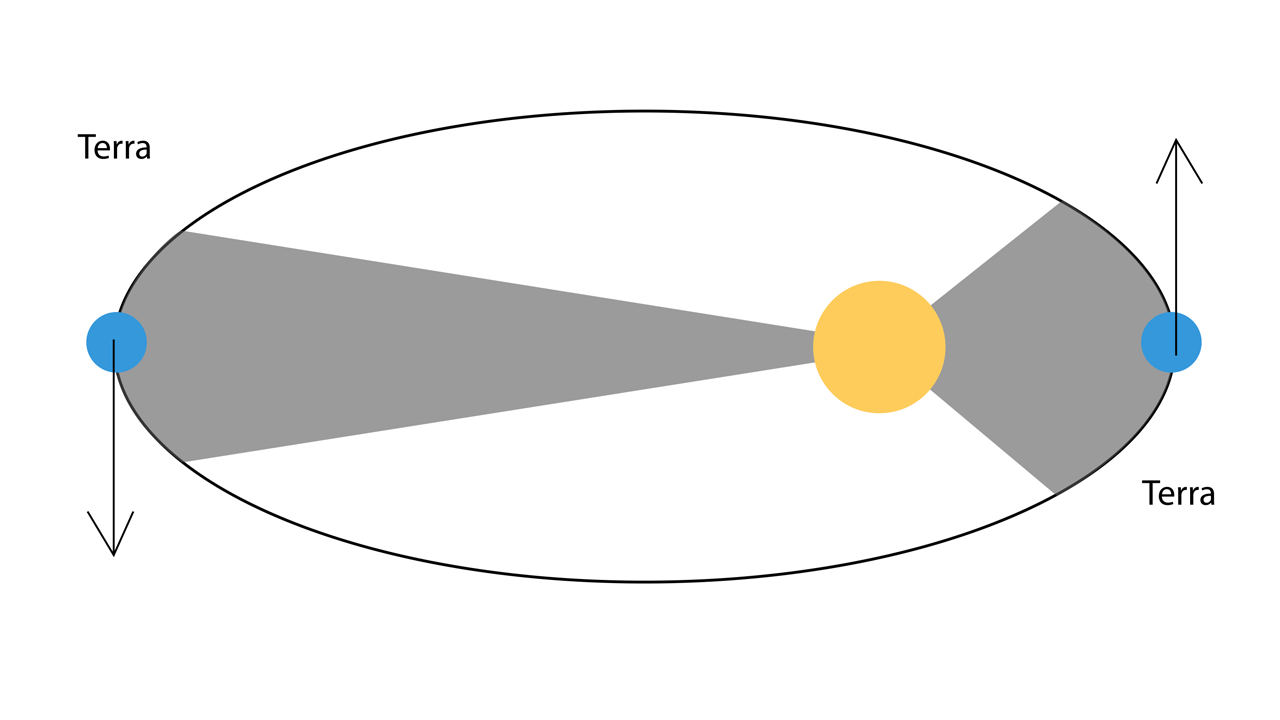
La prima legge di Keplero dice che:
«I pianeti seguono un’orbita ellittica avente il Sole in uno dei due fuochi.»
Keplero concepì un modello eliocentrico in cui le orbite non erano più circolari come nel sistema copernicano, ma ellittiche. Questa ulteriore novità provenne dalle accurate osservazioni riportate da Copernico e da Tycho Brahe nelle loro pubblicazioni. In particolare, gli accurati dati di Brahe sull’orbita di Marte, permisero a Keplero di accreditare il sistema eliocentrico e di formulare e affermare le proprie leggi.
Per la prima legge di Keplero, la distanza della Terra, quindi di qualsiasi altro pianeta dal Sole, non è costante ma varia lungo l’orbita. Il punto in cui un pianeta si trova più distante dal Sole è detto afelio, mentre il punto in cui l’orbita è più vicina, si chiama perielio.
I moti dei pianeti avvengono su un piano detto piano orbitale. Per la Terra tale piano è detto eclittica.
La prima legge di Keplero è fondamentale perché sancisce il primo punto di separazione definitivo della teoria eliocentrica di Copernico dalla teoria geocentrica precedente.
Le caratteristiche delle orbite ellittiche sono il semiasse maggiore, il semiasse minore, la semi-distanza focale, l’eccentricità.
L’eccentricità in un’ellisse è data dal rapporto tra la semi-distanza focale e il semiasse maggiore. I pianeti hanno eccentricità molto piccole: 0,0167 per la Terra, 0,0934 per Marte e 0,2482 per Plutone.
Curiosità: Tycho Brahe(1546-1601), astrologo e astronomo danese, dedicò la vita all’osservazione e ai calcoli delle orbite dei pianeti, fondamentali per Keplero e per l’astronomia del XVII secolo,pur non condividendo il sistema eliocentrico. L’astronomo danese aveva concepito un suo sistema detto ticiano, secondo cui il Sole girava attorno alla Terra immobile, e tutti gli altri pianeti orbitavano attorno al Sole.
Per ripassare vai alle lezioni sull’ellisse.
Seconda legge di Keplero
La seconda legge di Keplero:
«Il segmento che unisce il centro del Sole con il centro del pianeta, detto raggio vettore, copre aree uguali in tempi uguali»
Dalla seconda legge si deduce che un pianeta è più veloce al perielio e più lento all’afelio.
La velocità orbitale al perielio è maggiore di quella all’afelio perché la porzione di orbita che il pianeta percorre nello stesso intervallo di tempo è maggiore.
Tutto ciò è dovuto al fatto che l’area coperta dal raggio vettore in un tempo £$t$£ lungo una qualsiasi porzione di orbita è sempre uguale.
Terza legge di Keplero
La terza legge di Keplero:
«I quadrati dei tempi che i pianeti impiegano a percorrere le loro orbite sono proporzionali al cubo delle loro distanze medie dal Sole»
Il rapporto tra il quadrato del periodo di rivoluzione e il cubo del semiasse maggiore dell’orbita è lo stesso per tutti i pianeti.
Matematicamente questa legge può essere rappresentata nel seguente modo:
£$T^{2}=kr_m^{3}$£
dove:
- £$r_m$£ è il semiasse maggiore dell’orbita
- £$T$£ è il periodo di rivoluzione
- £$k$£ è un valore che dipende dal corpo celeste attorno al quale avviene il moto di rivoluzione
Si può dimostrare partendo dalla forza di attrazione gravitazionale tra due corpi di cui uno in moto attorno all’altro con un’accelerazione centripeta £$a_{cp}$£, che £$k=\frac {4\pi^2}{G \cdot M_c}$£ dove:
- £$G$£ è la costante di gravitazione universale
- £$M_c$£ è la massa del corpo attorno a cui avviene il moto di rivoluzione di un’altra massa, per la Terra £$M_{Sole}$£
La terza legge vale anche per i satelliti che orbitano intorno ai pianeti. Nel caso della Terra e la Luna, per esempio, £$K$£ dipende dalla massa della Terra £$M_{Terra}$£ mentre il valore del raggio £$r_m$£ è uguale alla distanza tra il centro della Terra e quello della Luna.
