L’accelerazione gravitazionale: cos'è e cosa comporta

L’accelerazione gravitazionale è un concetto fondamentale nella fisica che rappresenta la forza invisibile con cui la Terra ci “attira" verso di essa, ma non solo. È un fenomeno che si manifesta in ogni angolo dell’universo e determina come i corpi celesti interagiscano tra loro.

Da una semplice mela che cade da un albero, alle complesse traiettorie dei pianeti intorno alle stelle, l’accelerazione gravitazionale gioca un ruolo cruciale: questa forza invisibile e costante ha influenzato la nostra storia scientifica, ha ispirato leggende e racconti, e ha spinto l’umanità a interrogarsi sulla vera natura dell’universo. Scopriamo insieme cos’è e cosa comporta!

• L'accelerazione gravitazionale su Marte
• Come misurare l’accelerazione di gravità sulla Terra
• Problemi di misurazione dell’accelerazione di gravità
• Altri problemi di misurazione dell’accelerazione di gravità

L’accelerazione gravitazionale su Marte

Immaginiamo un uomo che deve viaggiare su Marte: quale sarà il problema più grave che dovrà affrontare?

• L’acqua? No, è stato dimostrato che l’acqua, nella sua fase solida, è presente sul pianeta sia nelle calotte polari sia nel sottosuolo. Procurarsela sarebbe un’importante sfida ingegneristica, ma non un’impossibilità.
• L’"aria"? O meglio, l’ossigeno? Di ossigeno molecolare, in atmosfera, su Marte ce n’è pochissimo. La pressione atmosferica del pianeta, inoltre, è lo 0.6% di quella terrestre. Eppure, se l’uomo vivesse in biomi pressurizzati e/o nel sottosuolo, e ricavasse ossigeno dal ghiaccio d’acqua locale o da piante importate dalla Terra, avremmo di nuovo un’importante sfida ingegneristica, ma non un’impossibilità.
• I raggi cosmici? Un problema reale, in mancanza di ozono nell’atmosfera marziana e pur tenendo conto della maggiore distanza del pianeta dal sole. Eppure di nuovo, costruendo habitat ben isolati e/o nel sottosuolo, torneremmo ad avere un’importante sfida ingegneristica, ma non un’impossibilità.
• E allora qual è il problema? L’accelerazione di gravità, su Marte, è £$3,71 \frac{\text{m}}{\text{s}^2}$£, ossia 0.38 volte quella terrestre, poco più di un terzo del nostro caro £$9,81 \frac{\text{m}}{\text{s}^2}$£. Tutte le forme di vita terrestri sono evolute per una £$g=9.81 \frac{\text{m}}{\text{s}^2}$£: il nostro metabolismo, dalla circolazione del sangue alla sudorazione alla digestione, è intimamente terrestre in senso gravitazionale, al punto che gli astronauti sulla Stazione Spaziale Internazionale, in ambiente di microgravità (quindi assai inferiore a quella marziana), sono essi stessi materia di esperimento per le reazioni della fisiologia umana alla quasi assenza di gravità. Per questa ragione non possono rimanere a lungo sulla ISS e la massima permanenza al momento permessa è 6 mesi.

Come misurare l’accelerazione di gravità sulla Terra

£$F=mg$£ non è nient’altro che l’applicazione al caso particolare della gravità del secondo principio della dinamica, £$F=ma$£.
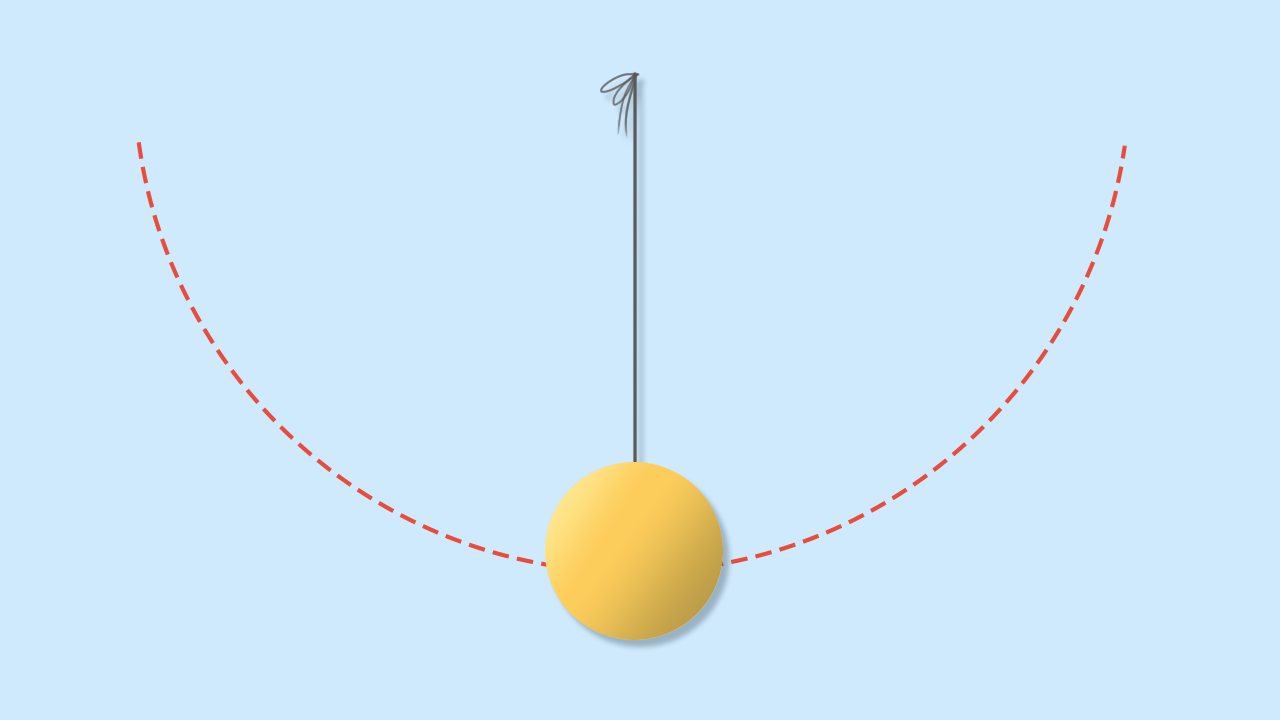
Sulla Terra (ma anche su Marte) possiamo misurare £$g$£ utilizzando un pendolo, realizzato con materiale di tutti i giorni: occorre un filo di cotone, due aste tenute insieme da un morsetto e fissate a un tavolo, una pesetto, un foglio di carta e una bilancia, un metro e un cronometro. Come sempre in fisica, il filo deve essere inestensibile, la masserella sufficientemente piccola, e le oscillazioni, a loro volta, sufficientemente piccole.

La legge che useremo è quella che lega il periodo del pendolo, £$T$£, alla lunghezza del filo £$l$£ e all’accelerazione di gravità terrestre, che dice che il periodo di oscillazione £$T$£ è uguale a £$2\pi$£ per la radice quadrata di £$\frac{l}{g}$£. Conseguentemente, £$g = 4\pi^2\frac{l}{T^2}$£.

Una volta montate le aste si procede a misurare la lunghezza del filo l, ad appendere il pesetto al filo e ad imporre al sistema una piccola oscillazione. Si procede dunque a misurare il periodo di oscillazione e si può ricavare la g del nostro pianeta.

Problemi di misurazione dell’accelerazione di gravità

Il pesetto oscillante appeso al filo è soggetto a 3 Forze:

• quella di gravità, £$F=mg$£,
• la trazione che lo vincola al filo, nella sua componente opposta in verso all’accelerazione di gravità, ossia £$F=T\cos \theta$£, ove £$\theta$£ è proprio l’angolo di oscillazione
• la forza opposta dall’attrito dell’aria, ma la consideriamo trascurabile sulla Terra e ancora di più su Marte, mentre sarebbe preponderante su Venere e su Titano. Ma non divaghiamo: niente attriti, dunque.

All’equilibrio, £$mg=T\cos \theta$£. Le oscillazioni £$\theta$£ devono essere piccole, in modo che il cosθ sia assimilabile a £$\theta$£; sperimentalmente, nell’ordine dei 5°, 10° al massimo. I 5-10° possono essere facilmente tracciati e visualizzati sul foglio di carta che, fissato sul pavimento, permette di avviare e seguire le oscillazioni.

Quante misure (di periodo, di £$l$£) devo effettuare per avere un risultato affidabile?
Ottima domanda. Se per una semplice misura di lunghezza sono sufficienti 1-3 misurazioni indipendenti, per una misurazione più complessa il numero di misure indipendenti deve essere maggiore. Innanzitutto, occorre misurare il periodo di almeno 10 oscillazioni, per garantire maggiore significatività statistica. Inoltre, occorrono almeno 3 misurazioni del periodo di 10 oscillazioni.

Quanto può essere pesante il pesetto?
In un semplice sistema da laboratorio, con un filo delle dimensioni di 1m, un pesetto compreso tra i 10g e 50g è più che sufficiente, per evitare sia modifiche alla struttura del filo, sia per garantire un’oscillazione adeguata alla situazione sperimentale.

Come dovrebbe oscillare il pendolo?
Tendenzialmente, l’oscillazione dovrebbe avvenire su un piano, ossia su due dimensioni, evitando il più possibile deviazioni da questa traiettoria ideale (buona fortuna!). Anche per questa ragione, e per l’impossibilità naturale di garantire siffatta oscillazione, 3 misurazioni indipendenti del periodo rappresentano un modo onesto di rafforzare la significatività della misurazione.

Altri problemi di misurazione dell’accelerazione di gravità

Che forma avrebbe il moto su Marte? Sarebbe diverso? Se sì, perché?
No, non sarebbe diverso. Sarebbe ovviamente diverso il risultato di £$g$£, e il moto apparirebbe leggermente più lento a parità di £$l$£ e £$m$£, ma la forma dell’oscillazione non avrebbe alcuna ragione fisica di essere diversa.

E se ci fosse attrito? Ossia, se l’esperimento lo stessimo facendo su Venere, che ha una pressione superficiale 92 volte maggiore di quella terrestre?
Su Venere, anche ammesso che l’intero sistema non sia corroso dagli acidi e incenerito/fatto sublimare dalla temperatura, non sarebbe possibile trascurare l’attrito dell’aria. Il nostro sistema sarebbe quindi fortemente smorzato e l’oscillazione assai più irregolare. La £$g$£ di Venere è, invece, assai simile a quella terrestre, ed è pari a £$8,87 \frac{\text{m}}{\text{s}^2}$£.

E, a proposito di questo, la temperatura a cui si effettua l’esperimento influisce sul risultato? Se sì, come?
Un significativo incremento di temperatura modificherebbe le caratteristiche fisiche del sistema, a cominciare dalla lunghezza del filo. In secondo luogo, significativi cambiamenti nella temperatura modificano la densità dell’aria, con possibili variazioni nella forza d’attrito.