I moti parabolici: definizione e formule pratiche
Il moto parabolico è conosciuto anche come il moto del proiettile, perché rappresenta il moto di un corpo che parte con una velocità iniziale e una certa angolazione per poi percorrere una traiettoria che assume la forma di una parabola, in quanto soggetta all’azione dell’accelerazione di gravità.
Scopriamo insieme cos’è il moto parabolico, come si definisce e quali sono le formule!
Vuoi testare la tua preparazione? Rispondi alle domande del nostro quiz!
- Cos'è il moto parabolico
- Il moto parabolico di un oggetto lanciato in orizzontale
- Il moto con velocità obliqua
- Leggi orarie del moto parabolico
Cos’è il moto parabolico
È molto semplice dare una definizione a questa tipologia di moto: il moto parabolico si definisce tale in quanto si tratta del moto di un corpo che segue una traiettoria parabolica in quanto soggetto solo ed esclusivamente della accelerazione di gravità. In fisica, infatti, vicino alla superficie terrestre possiamo affermare che quando i corpi cadono subiscono una accelerazione verso il basso che possiamo definire come accelerazione di gravità.
Questa accelerazione viene indicata come £$g$£ ed è pari a £$9,8 m/s^2$£. Si tratta di una accelerazione uniforme, cioè uguale in tutti i punti dello spazio preso in considerazione.
Il moto parabolico è anche detto moto del proiettile, sia perché i proiettili seguono questo moto e sia perché nel passato tutti i corpi che si muovevano secondo una traiettoria parabolica erano definiti in questo modo.
Per chiarire meglio, basti pensare ad un pallone: quando si calcia un pallone, questo si solleva da terra ma successivamente dopo aver raggiunto il picco di altezza tornerà a scendere descrivendo spesso un vero e proprio moto parabolico.
Il moto parabolico, in particolare, è un moto bidimensionale perché si compone di due moti rettilinei e simultanei:
- il moto rettilineo uniforme;
- il moto uniformemente accelerato.
Il moto parabolico di un oggetto lanciato in orizzontale

Se facciamo rotolare una pallina su un tavolo, cade seguendo una traiettoria parabolica.
Il moto della pallina è un moto bidimensionale lungo degli ipotetici assi x e y. Per poter studiare questo moto bisogna individuare le diverse leggi orarie che si verificano lungo questi due assi.
Lungo l’asse x il moto del corpo è rettilineo uniforme, in cui £$x$£ indica lo spazio orizzontale percorso e £$v_x$£ è la velocità orizzontale dell’oggetto, diversa da 0.
La legge oraria del moto è:
£$x = v \cdot t $£
Lungo l’asse y il moto del corpo segue la legge oraria di un corpo che cade verso il basso, quindi uniformemente accelerato in cui la £$v_{i} = 0$£ e lo spazio £$S$£ è l’altezza da cui parte il corpo considerato.
La legge oraria del moto è:
£$\begin{cases} S = \frac {1}{2} g · t^{2} \\ x = v_x \cdot t \end{cases}$£
La traiettoria del moto nella sua totalità è, quindi, un ramo di parabola e il punto di partenza del moto è il vertice della parabola considerata.
Il moto con velocità obliqua
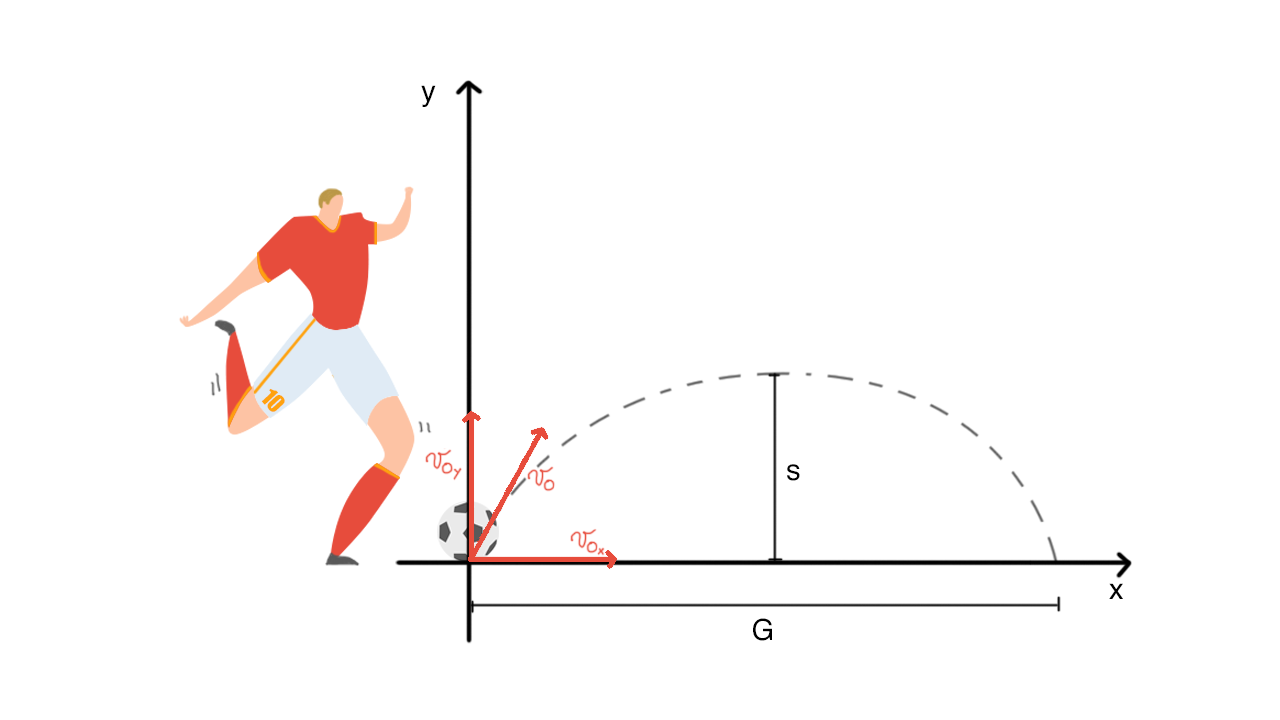
Come fa Totti a fare il “cucchiaio" quando batte i rigori? Usa la fisica!
Il pallone compie una traiettoria parabolica grazie al fatto che il calciatore gli imprime una velocità obliqua £$v_{0}$£ di inclinazione £$\alpha$£ rispetto al suolo. Spesso questo tipo di moto, insieme al moto parabolico con £$v_i$£ orizzontale è detto moto di un proiettile.
Questo è un moto bidimensionale lungo un ipotetico asse x e un ipotetico asse y.
Durante questo moto il corpo è soggetto solo all’accelerazione di gravità £$g$£ e agli attriti dell’aria, che possono essere trascurati.
Essendo un moto bidimensionale, per poterlo studiare bisogna individuare le diverse leggi orarie che si verificano lungo l’asse x e y e quindi bisogna scomporre la velocità, che, essendo obliqua, è formata da una componente £$v_{x_0}$£ lungo l’asse x e da una componente £$v_{y_0}$£ lungo l’asse y:
- La componente lungo l’asse x è: £$v_{x_0} = v_{0} · \cos{\alpha}$£
- La componente lungo l’asse y è: £$v_{y_0} = v_{0} · \sin{\alpha}$£
L’angolo £$\alpha$£ è l’angolo acuto compreso tra il vettore £$v_0$£ e la retta del suolo.
Leggi orarie del moto parabolico
Lungo l’asse £$x$£ il moto è un moto rettilineo uniforme in cui la velocità sarà la componente £$v_{x_0}$£ della velocità iniziale £$v_{0}$£ e lo spazio £$S$£ sarà la gittata, ovvero la distanza orizzontale totale percorsa dal corpo.
La legge del moto lungo l’asse £$x$£ è:
$$x = v_{x_0} · t$$
Per la gittata esiste una formula alternativa che è:
$$G = \frac{2 v_{0}^2 \sin\alpha \cos\alpha}{g} $$
La legge del moto lungo l’asse £$y$£ è quello di un corpo lanciato verso l’alto e lo dividiamo quindi in due parti:
Nella prima parte il moto è uniformemente decelerato in cui la decelerazione è pari all’opposto dell’accelerazione gravitazionale £$g$£ e lo spazio è pari all’altezza massima raggiunta dal corpo. Nel momento in cui il corpo raggiunge l’altezza massima la sua velocità è nulla e inizierà a precipitare verso il basso.
La legge oraria lungo l’asse £$y$£ della prima parte del moto è:
$$\begin{cases} S = -\frac {1}{2} g \cdot t^{2} + v_{y_0} \cdot t \\ v_{F} = -g \cdot t + v_{y_0}\end{cases} $$
Nella seconda parte il moto sarà uniformemente accelerato con £$v_{i} = 0 $£ e spazio £$S$£ pari all’altezza in cui si trova.
La legge oraria lungo l’asse £$y$£ della seconda parte del moto è:
$$\begin{cases} S = \frac {1}{2} g \cdot t^{2} \\ v_{F} = g \cdot t \end{cases} $$
A parità di velocità £$v_0$£ si ottiene la gittata massima quando il vettore velocità iniziale è inclinato di 45° rispetto al suolo.
Il moto parabolico: la mappa concettuale
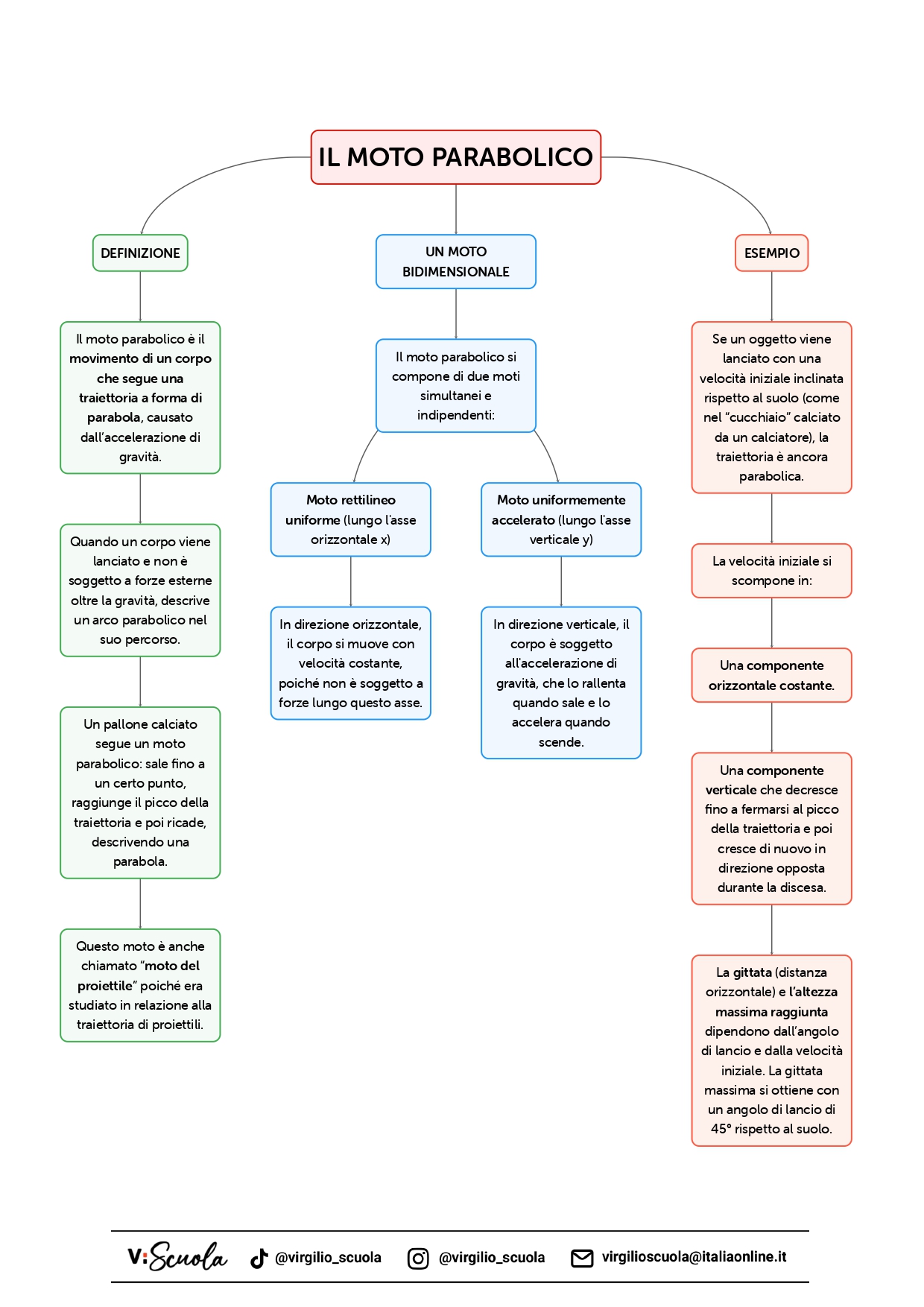
Questa mappa ti aiuterà a memorizzare facilmente i temi importanti. Scaricala e ripassa quando vuoi!
