Il pendolo in fisica: definizione e formule
Il pendolo semplice è un sistema fisico costituito da più elementi: un filo rigido, incomprimibile e inestensibile di massa nulla e un massa puntiforme, che invece ha una propria massa. Questa massa puntiforme è soggetta all’attrazione gravitazionale, quindi viene richiamata verso la superficie dalla forza di gravità, sebbene nel pendolo non sia presente attrito.
Questa tipologia di pendolo è definito semplice, mentre qualora il filo fosse sostituito da un corpo rigido, avremmo il pendolo composto. Il pendolo mantiene un’oscillazione costante, e proprio per questo possiamo osservare che descrive un moto armonico.
In questo articolo scopriremo meglio cos’è un pendolo, quali sono le sue caratteristiche e tutte le formule ad esso collegate!
Vuoi testare la tua preparazione? Tenta il nostro quiz!
- Caratteristiche del pendolo
- Il moto di un pendolo
- La forza del pendolo
- Il periodo del pendolo
- Il pendolo di Foucault
- Il pendolo in fisica: la mappa concettuale
Caratteristiche del pendolo
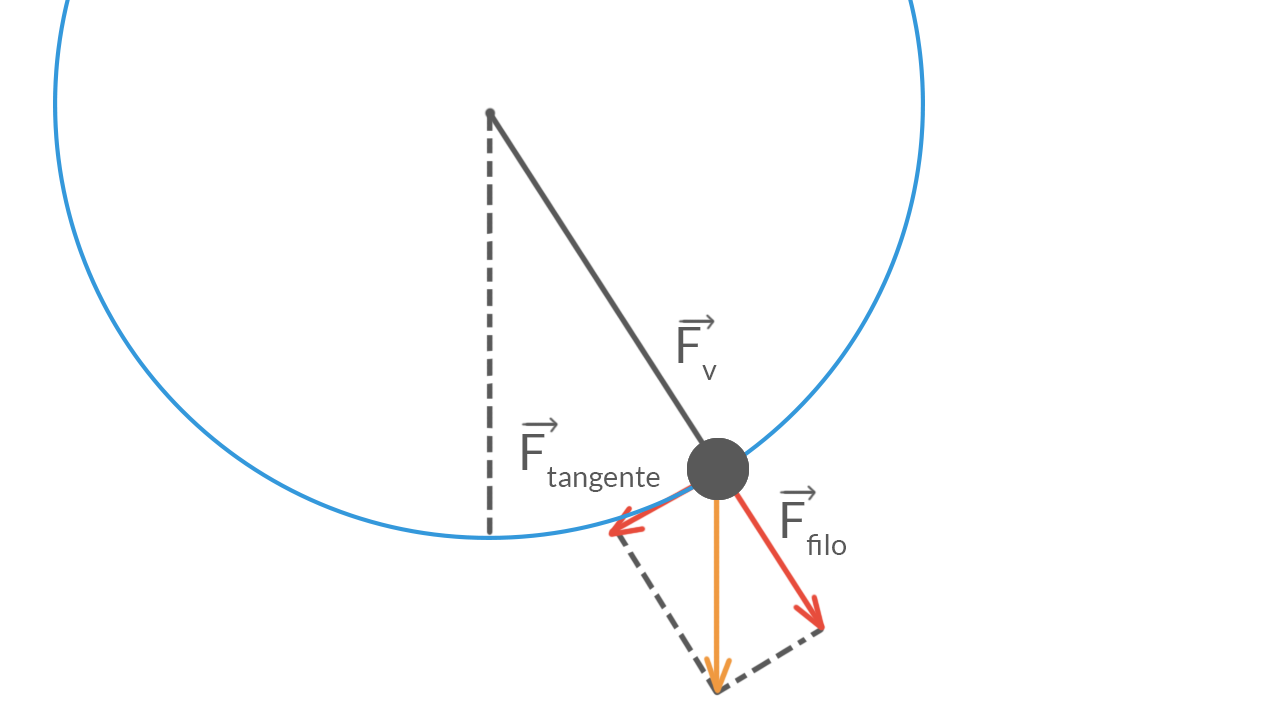
Il pendolo (una pallina appesa ad un filo) è composto da una massa £$m$£ che oscilla attaccata ad un filo inestensibile di massa trascurabile.
Un pendolo è in equilibrio quando la massa £$m$£ è ferma e il filo è perfettamente verticale.
Se la massa viene spostata dalla posizione di equilibrio (dalla verticale) inizierà ad oscillare lungo un piano verticale a causa del richiamo del suo peso che tenta di ricondurla nella posizione di equilibrio. Se non ci fossero attriti il pendolo oscillerebbe all’infinito (l’oscillazione continuerebbe uguale a se stessa).
Il pendolo è un esempio di oscillatore armonico poichè è soggetto ad una forza di richiamo direttamente proporzionale allo spostamento rispetto alla posizione di equilibrio.
La traiettoria descritta dal moto è un arco di circonferenza che ha centro nel punto di ancoraggio del filo e raggio pari alla lunghezza del filo stesso.
Il moto di un pendolo
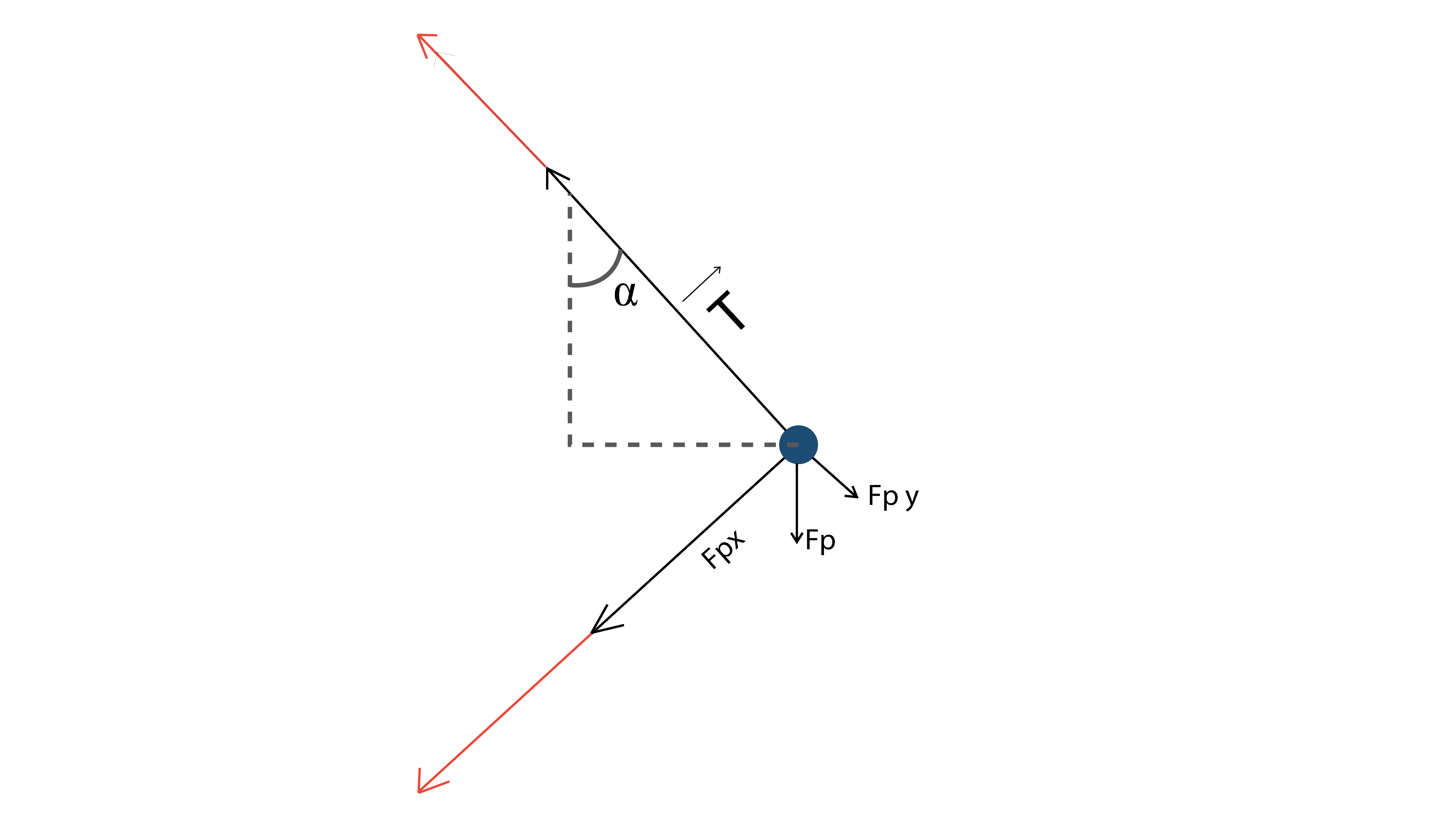
Per analizzare il moto di un pendolo occorre creare un sistema di riferimento cartesiano in cui:
- l’asse £$y$£ ha la stessa direzione del filo (di lunghezza L)
- l’asse £$x$£ è tangente alla traiettoria del moto.
Questo riferimento cartesiano non è fisso ma ruota seguendo il moto del corpo oscillante.
Quindi, la forza peso £$F_p$£ deve essere divisa nelle sue componenti x e y:
£$F_{p_y} = m \cdot g \cos\alpha $£ £$F_{p_x} = -m \cdot g \sin\alpha $£
La componente in £$y$£ viene controbilanciata dalla tensione £$T$£, quindi la risultante delle forze lungo l’asse y è nulla.
£$\vec{F}{p_y} = -\vec{T} $£
La componente in £$x$£ ha segno negativo perchè è una forza di richiamo che tende a riportare il corpo nella posizione di equilibrio e, infatti, è opposta al verso del moto.
La forza del pendolo
Dalla formula della componente in £$x$£ del peso £$F_{p_x} = -m \cdot g \sin\alpha $£ si deduce che questa forza è direttamente proporzionale a £$\sin\alpha $£.
Per angoli £$0°la componente in [iol_placeholder type="formula" engine="katex" display="inline"]x$£ è direttamente proporzionale all’angolo stesso.
£$\begin{cases} F_{p_x} = – m \cdot g \cdot \sin\alpha \\ \sin\alpha = \alpha \end{cases}$£ ⇒ £$ F_{p_x} = – m \cdot g \cdot \alpha$£
Questa approssimazione viene utilizzata, per semplicità di calcolo, anche con angoli maggiori di £$10°$£.
Allo stesso modo, per semplicità, anche lo spostamento del pendolo lungo l’asse £$x$£ può essere approssimato all’arco di circonferenza descritto durante il moto. Quindi:
se: £$\begin{cases} \sin\alpha = \frac {\overset{\displaystyle \frown}{AB}}{L} \\ \sin\alpha = \alpha \\ \overset{{\displaystyle \frown}}{AB} = x \end{cases}$£
allora: £$ \alpha = \frac{x}{L}$£ (dove L è la lunghezza del filo.)
Infine, riprendendo la formula inziale £$ F_{p_x} = – m \cdot g \cdot \alpha$£, sostituendo £$ \alpha = \frac{x}{L}$£, possiamo esprimere la forza del pendolo come:
£$ F_{p_x} = – m \cdot g \cdot \frac{x}{L}$£ oppure £$ F_{p_x} = – (\frac{m \cdot g}{L}) \cdot {x}$£
Attenzione!
Quest’ultima formula è analoga alla forza elastica, in questo caso la costante £$k$£ è £$\frac{m \cdot g}{L}$£ e si misura in £$\frac{N}{m}$£, proprio come la costante elastica della molla.
Il periodo del pendolo
Come si calcola il periodo del pendolo?
Ricaviamo dalla formula della forza del pendolo £$ F_{p_x} = – (\frac{m \cdot g}{L}) \cdot {x}$£ che la costante £$k$£ è pari a £$\frac{m \cdot g}{L}$£
Sostituiamo la costante nella formula del periodo del moto armonico della molla £$T = 2π \sqrt{\frac{m}{k}}$£
Ricaviamo che il periodo del pendolo è pari a £$T = 2π \sqrt{\frac{L}{g}}$£ (in cui £$L$£ è la lunghezza del pendolo).
Il pendolo di Foucault
Nel 1851 Foucault eseguì un esperimento con un pendolo di massa pari a £$30 Kg$£ e appeso ad una fune lunga £$68 m$£.
L’esperimento venne svolto nel Phanteon di Parigi e si notò che, a differenza di un pendolo ideale che oscilla sempre lungo un medesimo piano verticale, il pendolo di Foucalt, col passare del tempo, descrive un settore circolare.
L’esperimento aveva l’obiettivo di dimostrare l’esistenza della rotazione terrestre.
Non è il pendolo ad avere un oscillazione alterata rispetto al modello ideale ma è la Terra sottostante che, ruotando, è come se facesse ruotare il piano verticale su cui esso si muove.
Se la Terra fosse ferma, il pendolo dovrebbe tracciare un’unica linea sul pavimento. Nel corso dell’esperimento, lasciando oscillare il pendolo si vide che disegnava delle linee sotto di esso. Poiché il piano di oscillazione libera di un pendolo non cambia, le linee indicavano che era il terreno sottostante a muoversi.
Foucault dimostrò che l’angolo che raggruppava queste linee era in relazione alla latitudine del luogo; in particolare:
- all’equatore, l’angolo è nullo (la rotazione “non c’è" perché il piano del pendolo è perpendicolare all’asse di rotazione terrestre)
- al Polo Nord è di 360° (la Terra ruota sotto di lui facendo in 24 ore un giro completo, dando l’impressione che sia invece il pendolo a ruotare).
Attenzione!
Se la Terra fosse un sistema inerziale, il pendolo traccerebbe delle linee lungo la medesima direzione.
Il pendolo in fisica: la mappa concettuale
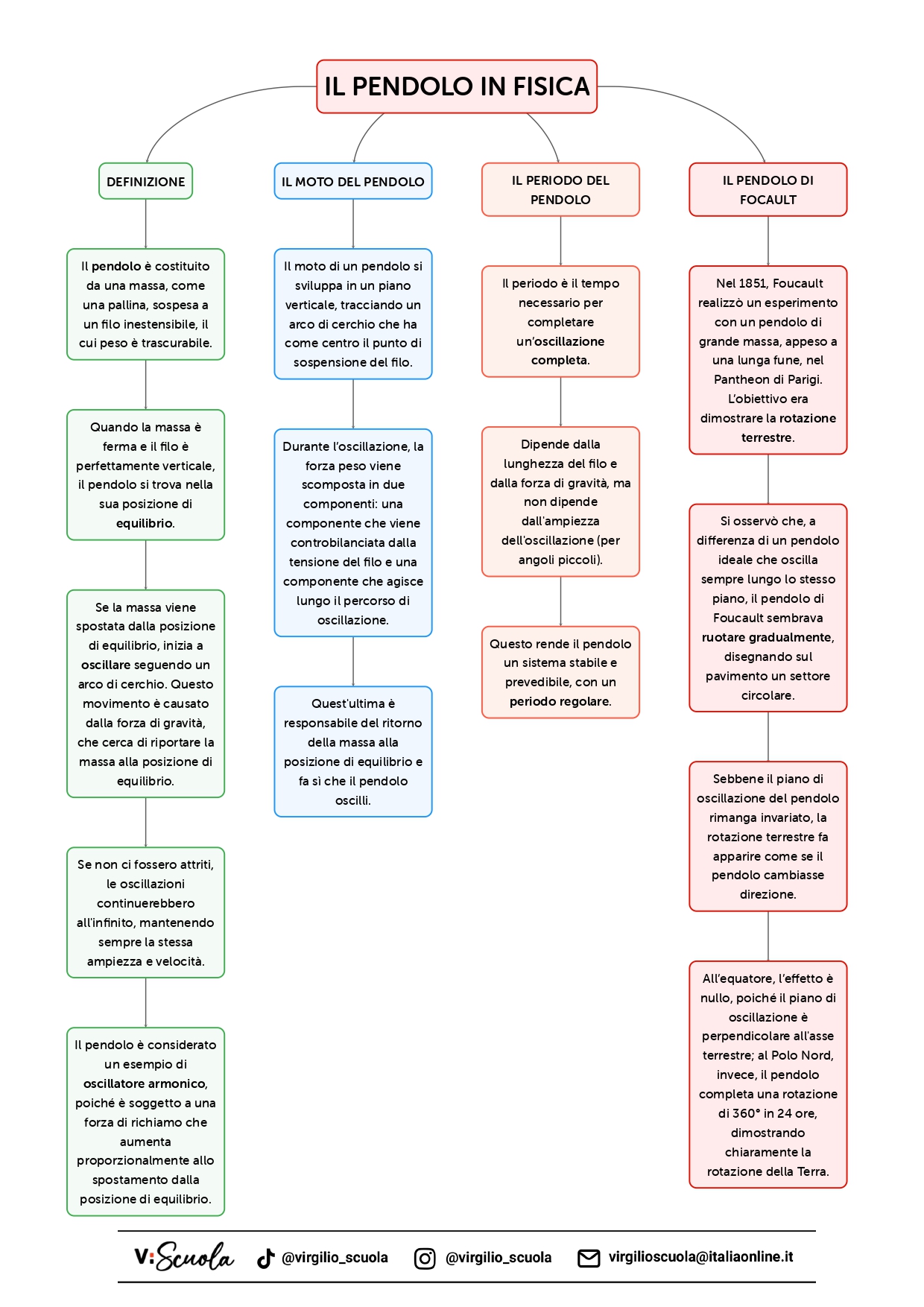
Scarica la mappa in formato PDF da portare sempre con te!
