Formulario di geometria solida: area e volume dei poliedri
I poliedri sono figure geometriche tridimensionali composte da facce poligonali, che si incontrano lungo i lati e si connettono nei vertici. Ogni poliedro ha una struttura unica definita dal numero e dalla forma delle sue facce, dai suoi spigoli e dai suoi vertici. Esistono vari tipi di poliedri, tra cui i poliedri regolari (dove tutte le facce sono poligoni regolari e congruenti), i poliedri irregolari e i poliedri composti.
Confondi la formula per trovare il volume del prisma con quella della piramide? Abbiamo noi la lezione che fa per te. Qui trovi tutte le formule di geometria solida riferite ai poliedri.
In questa lezione vedrai le formule per calcolare il volume e la superficie totale dei solidi e dei solidi di rotazione. Ecco quali poliedri troverai qui:
- cubo
- prisma retto
- piramide
- tronco di piramide
- Cos'è un poliedro
- Formula volume e superficie del cubo
- Formula volume e superficie del prisma retto
- Formula volume e superficie della piramide
- Formula area e superficie del tronco di piramide
Cos’è un poliedro
Un poliedro è una figura geometrica tridimensionale delimitata da facce poligonali che si incontrano lungo gli spigoli e i vertici. I poliedri possono avere varie forme e dimensioni, e alcuni esempi comuni includono il cubo, il prisma retto, la piramide e il tronco di piramide.
Cubo
Il cubo è un poliedro regolare costituito da sei facce quadrate congruenti, dodici spigoli di uguale lunghezza e otto vertici. È uno dei cinque solidi platonici e rappresenta una delle forme geometriche più simmetriche e regolari.
Prisma retto
Il prisma retto è un poliedro con due basi congruenti e parallele che sono poligoni, e le facce laterali sono rettangoli perpendicolari alle basi. Se le basi sono quadrate, il prisma è detto cubo; altrimenti, può avere basi di qualsiasi forma poligonale, come triangoli, pentagoni o esagoni.
Piramide
La piramide è un poliedro con una base poligonale e un vertice singolo non complanare. Le facce laterali della piramide sono triangoli che si uniscono al vertice comune. Le piramidi possono essere classificate in base alla forma della loro base, come piramidi triangolari, quadrate o pentagonali.
Tronco di piramide
Il tronco di piramide è una piramide che è stata tagliata da un piano parallelo alla base, rimuovendo così la parte superiore. Questo crea una figura con una base superiore e una base inferiore che sono poligoni simili, e le facce laterali sono trapezoidi. Il tronco di piramide mantiene le caratteristiche principali della piramide originale, ma ha una struttura più complessa con due basi.
Formula volume e superficie del cubo
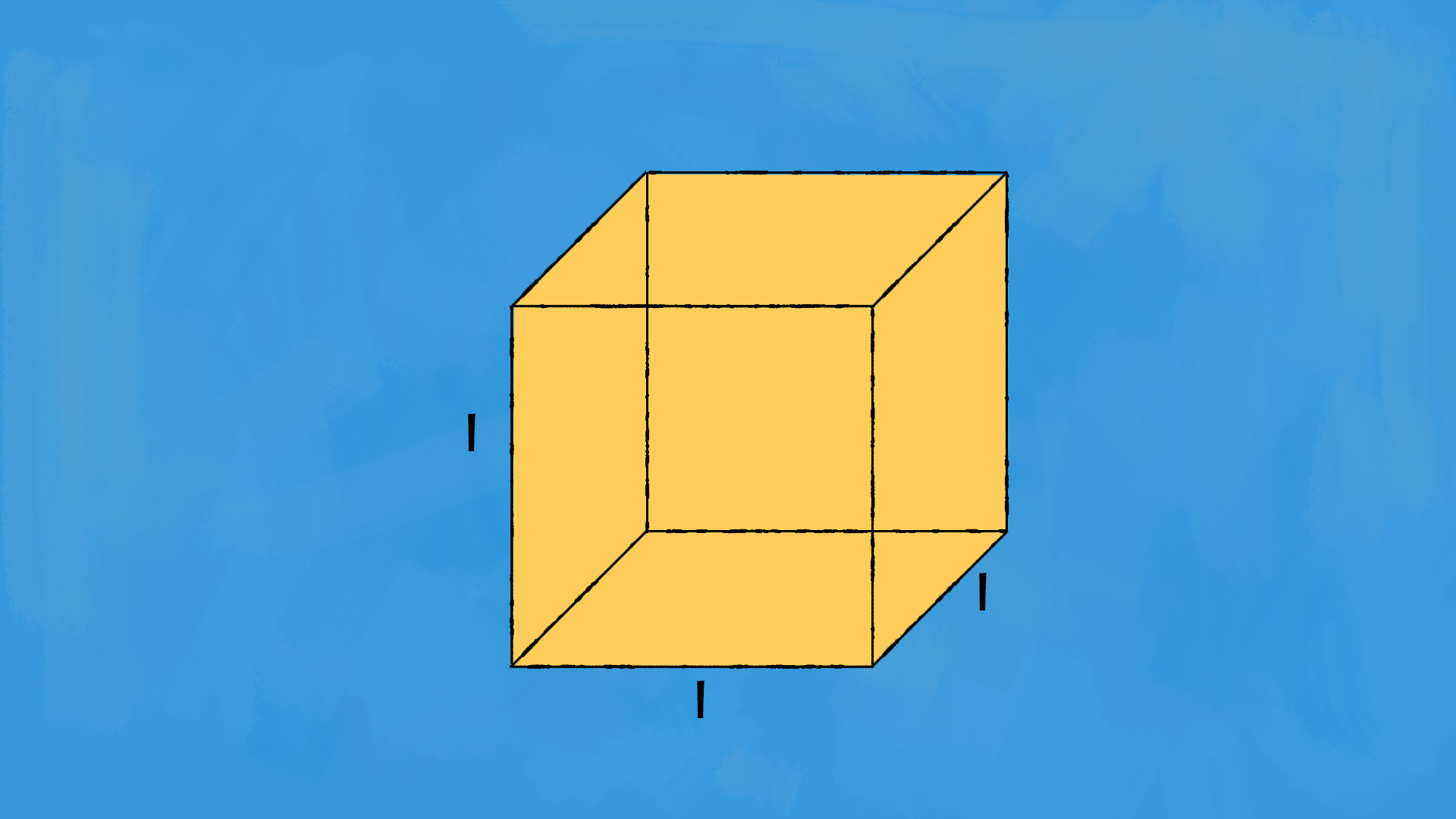
La superficie totale del cubo è $$S_{TOT}=6\cdot l^2$$
Il volume del cubo è $$V=l^3$$
Formula volume e superficie del prisma retto
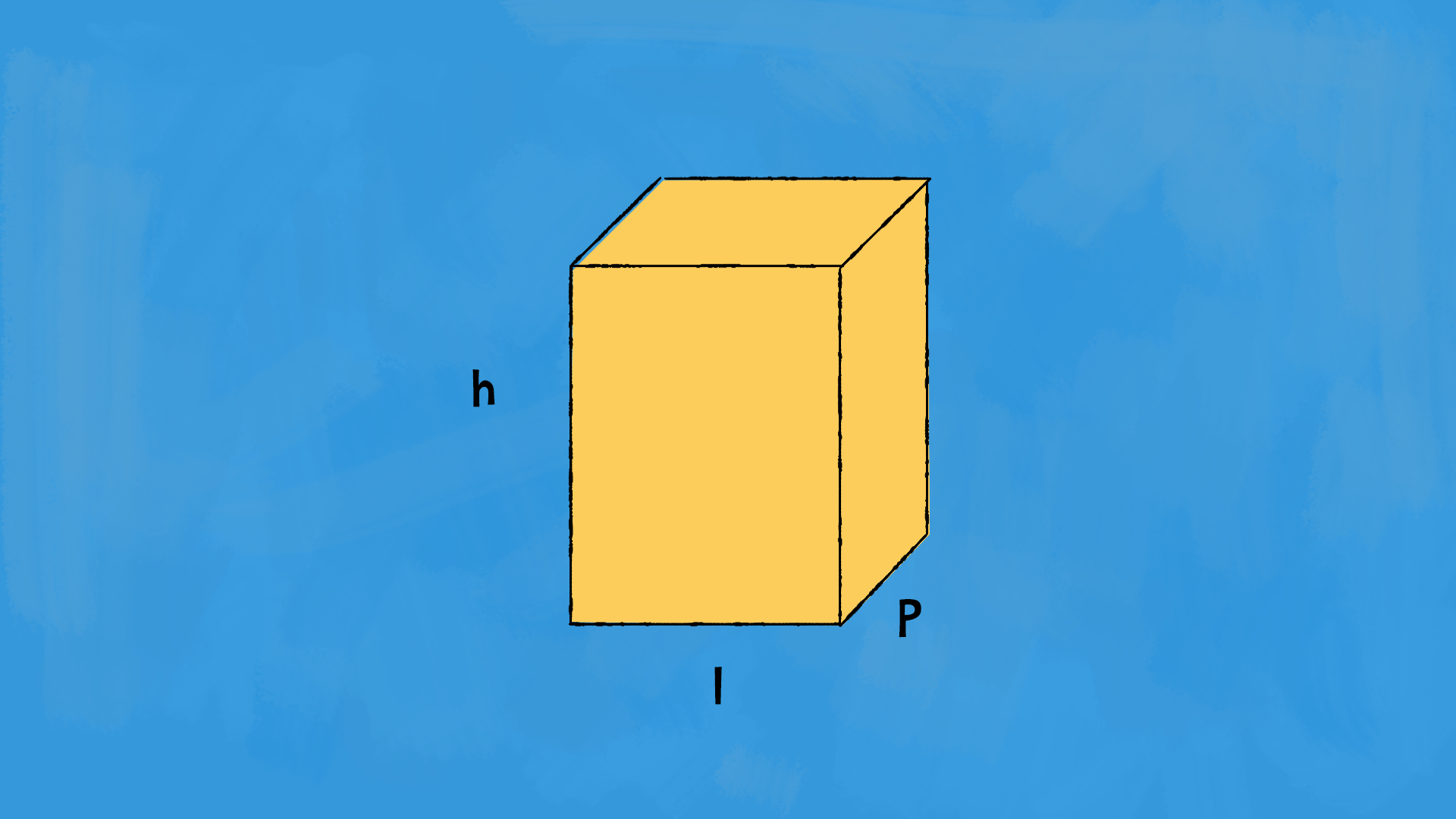
La superficie di base £$S_b$£dipende dal poligono di base del prisma.
La superficie laterale è $$S_l=2p\cdot h$$
La superficie totale misura $$S_{TOT}=2\,S_b+S_l$$
Il volume del prisma è $$V=S_b\cdot h$$
Formula volume e superficie della piramide
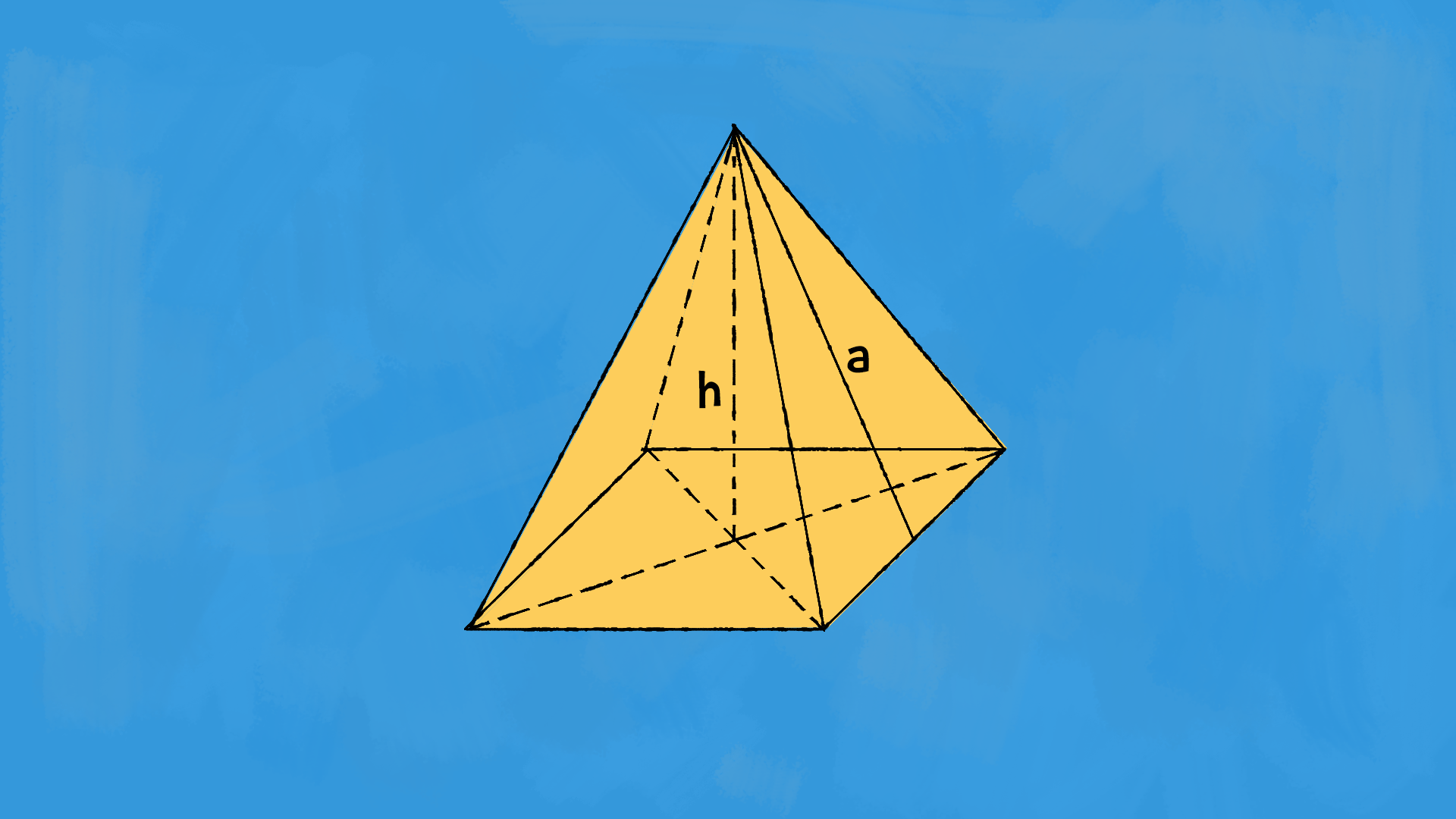
La superficie di base £$S_b$£dipende dal poligono di base della piramide.
La superficie laterale è $$S_l=\frac{2p\cdot a}{2}$$
La superficie totale misura $$S_{TOT}=S_b+S_l$$
Il volume della piramide è $$V=\frac{S_b\cdot h}{3}$$
Formula area e superficie del tronco di piramide
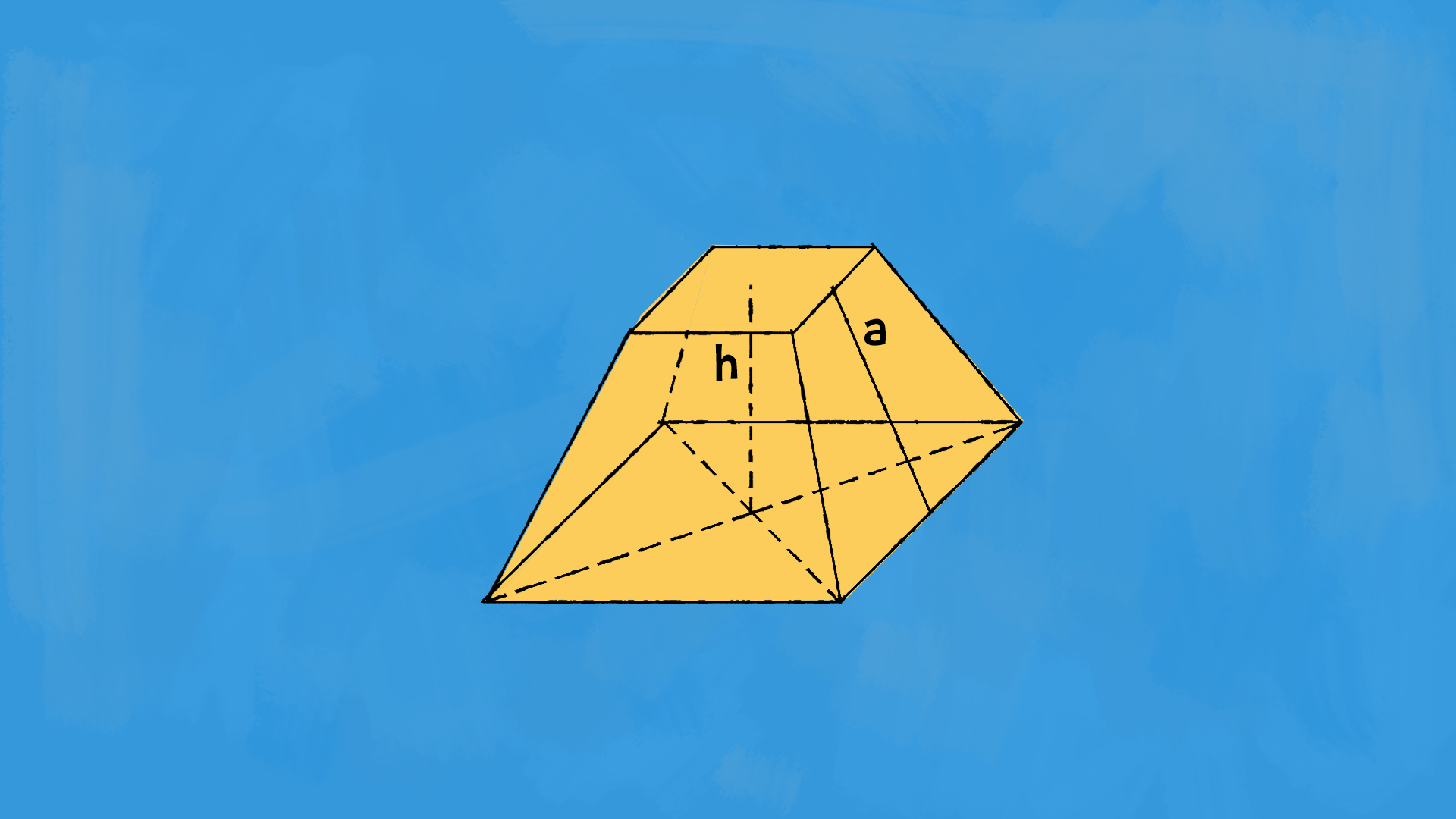
Le superfici di base £$S_{b1}$£ e £$S_{b2}$£ dipendono dai poligoni di base del tronco di piramide.
La superficie laterale è $$S_l=\frac{(2p_1+2p_2)\cdot a}{2}$$
La superficie totale misura $$S_{TOT}=S_{b1}+S_{b2}+S_l$$
Il volume del tronco di piramide è $$V=\frac{\left( S_{b1}+S_{b2}+\sqrt{S_{b1}+S_{b2}} \right) \cdot h }{3}$$
