Formulario di geometria piana: triangolo, poligoni, circonferenza
Scopri quali sono le formule dirette per calcolare l’area del triangolo, dei poligoni regolari e della circonferenza! Vedrai anche le formule inverse così non avrai più dubbi negli esercizi di geometria piana.
In questa lezione troverai le formule dell’area e le formule inverse di:
- triangolo
- poligoni regolari
- circonferenza
- Perché è importante avere un formulario di geometria piana
- Caratteristiche di triangolo, poligoni regolari e circonferenza
- Formula area del triangolo
- Formula area poligoni regolari
- Formula area circonferenza
Perché è importante avere un formulario di geometria piana
Avere a disposizione un formulario di geometria piana è fondamentale per avere un accesso rapido e organizzato a definizioni, teoremi e formule essenziali.
Questo strumento permette di risolvere problemi matematici con efficienza e precisione. Un formulario ben strutturato aiuta a comprendere le relazioni tra diverse forme geometriche e le loro proprietà, facilitando il calcolo di aree, perimetri, angoli e altri attributi importanti.
Inoltre, rappresenta una guida durante gli esami o in situazioni professionali dove il tempo è limitato: non è solo uno strumento di consultazione, ma un indispensabile alleato nell’apprendimento e nell’applicazione pratica della geometria.
Caratteristiche di triangolo, poligoni regolari e circonferenza
Ecco un riassunto delle caratteristiche di triangoli, poligoni regolari e circonferenze:
Triangolo
Il triangolo è una figura geometrica piana composta da tre lati e tre angoli. La somma degli angoli interni di un triangolo è sempre uguale a 180 gradi. I triangoli possono essere classificati in base alla lunghezza dei loro lati (isoscele, equilatero, scaleno) o in base ai loro angoli (rettangolo, acuto, ottuso). Ogni triangolo ha una serie di assi di simmetria a seconda del suo tipo, e il concetto di triangoli è fondamentale in molte aree della geometria.
Poligoni regolari
Un poligono regolare è una figura geometrica piana chiusa con lati e angoli uguali. Il numero dei lati determina il nome specifico del poligono (es. pentagono per 5 lati, esagono per 6). I poligoni regolari sono equiangolari (tutti gli angoli sono uguali) ed equilateri (tutti i lati hanno la stessa lunghezza).
Circonferenza
La circonferenza è una curva piana chiusa e perfettamente rotonda, definita come l’insieme dei punti in un piano che sono a una distanza fissa, detta raggio, da un punto dato, chiamato centro. La circonferenza è la base per la definizione di altre forme rotonde come il cerchio, che comprende la regione interna delimitata dalla circonferenza.
Formula area del triangolo
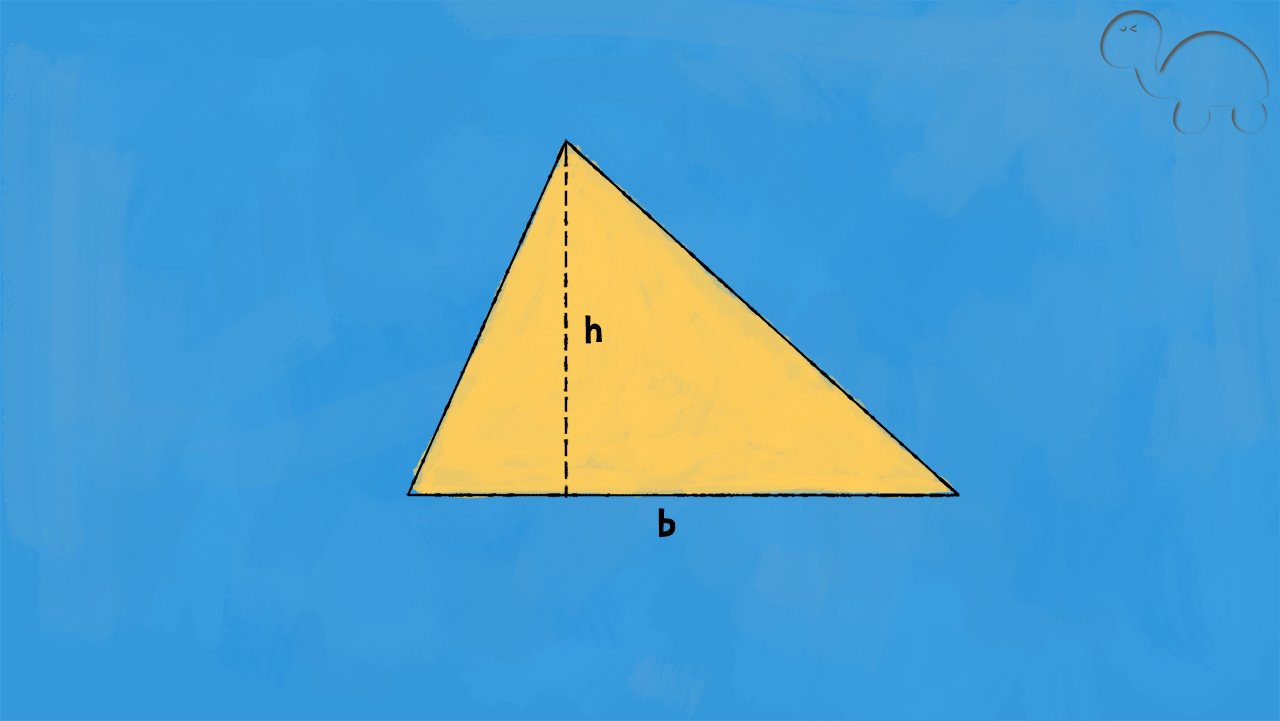
La formula diretta è $$A=\frac{b\cdot h}{2}$$
Le formule inverse sono
$$b=\frac{2A}{h}$$ $$h=\frac{2A}{b}$$
Formula area poligoni regolari
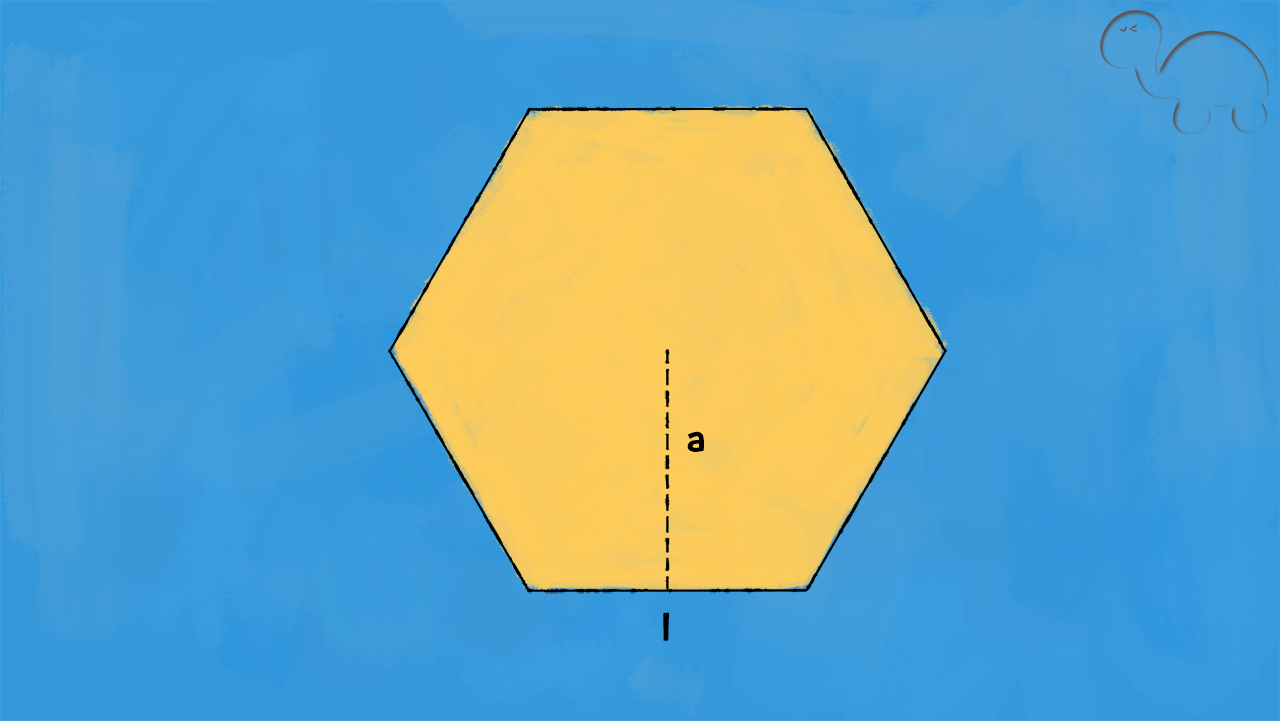
La formula diretta è $$A=\frac{2p\cdot a}{2}$$
Le formule inverse sono
$$2p=\frac{2A}{a}$$ $$a=\frac{2A}{2p}$$
dove £$2p$£ indica il perimetro e £$a$£ l’apotema del poligono regolare.
Formula area circonferenza
La formula diretta dell’area è $$A=\pi r^2$$
La formula inversa è
$$r=\sqrt{\frac{A}{\pi}}$$
La lunghezza della circonferenza misura $$C=2\pi\,r$$