Teoremi e proprietà del triangolo isoscele
Il triangolo isoscele è una figura geometrica fondamentale, caratterizzata dall’avere due lati di uguale lunghezza.
Questa proprietà conferisce al triangolo isoscele una simmetria unica rispetto all’altezza che cade sul lato disuguale, detto base. Oltre alla simmetria visiva, il triangolo isoscele si distingue per le sue particolarità matematiche, come angoli uguali alla base.
Vuoi imparare tutte le proprietà dei triangoli isosceli? Sei nella lezione giusta! Hai imparato a classificare i triangoli e i criteri di congruenza, ora puoi imparare le loro proprietà più importanti: il Teorema del triangolo isoscele e il suo Teorema inverso.
- Teorema del triangolo isoscele
- Bisettrice nei triangoli isosceli
- Cosa potrebbero chiederti nell'interrogazione
- Sfida sui triangoli isosceli
Teorema del triangolo isoscele
Enunciato e dimostrazione
Ipotesi e tesi del teorema
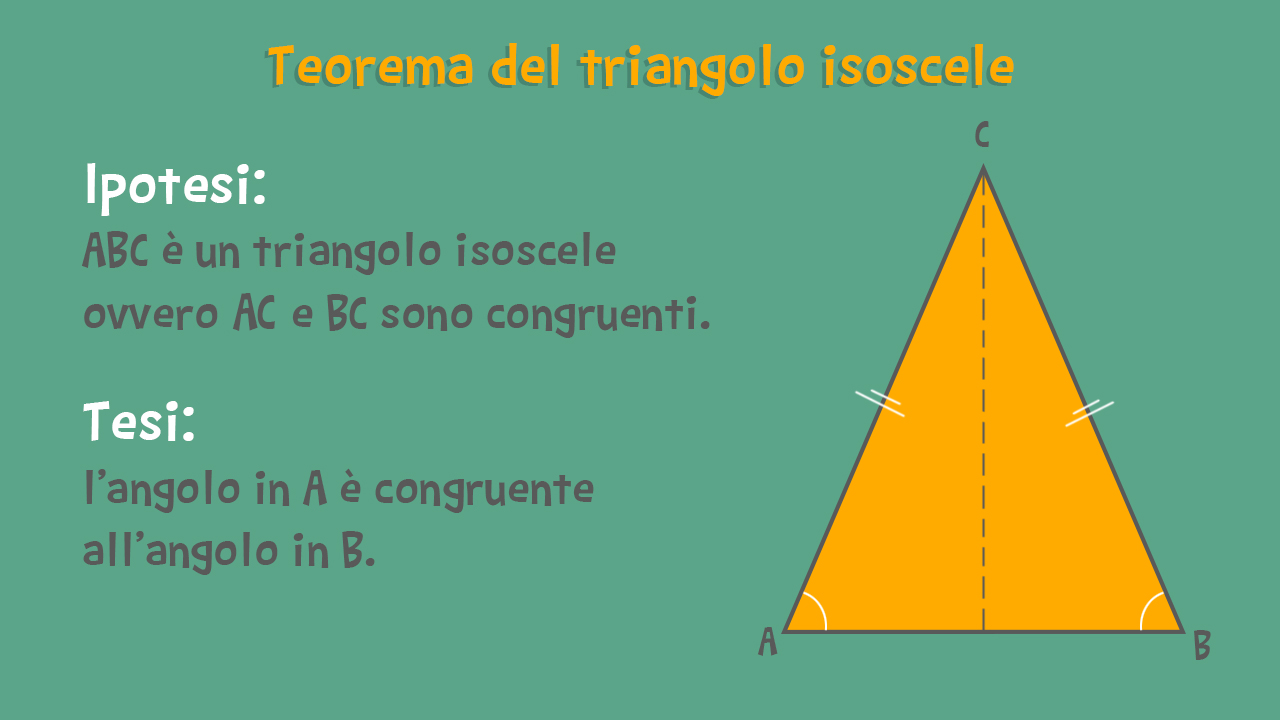
I triangoli isosceli sono quelli con due lati congruenti.
Teorema del triangolo isoscele:
Se un triangolo è isoscele, allora ha (anche) due angoli congruenti.
Per dimostrare il teorema del triangolo isoscele, tracciamo la bisettrice dell’angolo opposto alla base e troviamo così due nuovi triangoli: a questi applichiamo il primo criterio di congruenza per concludere che i due angoli alla base sono congruenti.
Inverso del teorema del triangolo isoscele:
Se un triangolo ha due angoli congruenti allora è isoscele … ha quindi anche due lati congruenti.
Per dimostrare l’inverso del teorema del triangolo isoscele prolunghiamo i due lati obliqui (quelli uguali!) di due segmenti congruenti, poi applichiamo il teorema del triangolo isoscele appena dimostrato e i primi due criteri di congruenza ai triangoli che abbiamo ottenuto con la nostra costruzione.
Il teorema del triangolo isoscele e il suo inverso si possono scrivere in un solo enunciato:
“Condizione necessaria e sufficiente affinché un triangolo sia isoscele è che abbia due angoli congruenti"
Quindi se è isoscele (ha due lati uguali) ha due angoli uguali, e se ha due angoli uguali è isoscele (ha due lati uguali).
Bisettrice nei triangoli isosceli
Le proprietà della bisettrice
Bisettrice, altezza e mediana

Nei triangoli isosceli: la bisettrice dell’angolo al vertice è anche mediana e altezza.
La dimostrazione di questa proprietà dei triangoli isosceli è simile a quella del teorema del triangolo isoscele, tracciamo la bisettrice, applichiamo il primo criterio di congruenza ai due triangoli che abbiamo così costruito e analizziamo i segmenti e gli angoli rimasti per concludere che la bisettrice è anche mediana e altezza!
Applicazione al teorema del triangolo equilatero
Un triangolo è equilatero quando ha tutti i lati congruenti. Ogni triangolo equilatero è anche isoscele perché ha due lati congruenti. La conseguenza è che possiamo applicare al triangolo equilatero i teoremi del triangolo isoscele:
- condizione necessaria e sufficiente affinché un triangolo sia equilatero è che abbia i tre angoli congruenti (dal teorema del triangolo isoscele);
- in un triangolo equilatero ogni bisettrice è anche mediana e altezza (dal teorema della bisettrice del triangolo isoscele).
Cosa potrebbero chiederti nell’interrogazione
Se ti chiedi sempre cosa potrebbe chiederti il tuo prof nell’interrogazione, questo è il video giusto per te! Ecco una simulazione di interrogazione sul triangolo isoscele e le sue proprietà!
Sfida sui triangoli isosceli
Sfida:
Soluzione:
Capitan Uncino sta progettando una nuova bandiera: ha la forma di un triangolo isoscele e il simbolo è un triangolo ottenuto unendo i punti medi dei tre lati. Questo simbolo è un triangolo isoscele? Prova a risolvere la sfida!
