Disposizioni: definizione, tipologie e applicazioni

Agostino Sapienza

INSEGNANTE DI MATEMATICA

Sono nato a Reggio Calabria il 07/10/85. Mi sono diplomato nel 2005 all'Istituto Magistrale Statale Tommaso Gulli. Ho conseguito la laurea triennale in Relazioni Internazionali a Messina e in Economia Internazionale a Padova. Dopo un pò di anni negli studi commercialisti sono stato chiamato per una supplenza covid nella classe di insegnamento A47. Ho poi conseguito l'abilitazione a Trieste nel sostegno e sono entrato di ruolo nel 2023

Le disposizioni sono uguali alle permutazioni ma consideriamo solo una parte degli elementi, non tutti. Quindi abbiamo delle sequenze ordinate di lunghezza minore del numero di elementi possibili che possiamo utilizzare. Possiamo trovare disposizioni semplici e disposizioni con ripetizione.

Che differenza c’è tra le disposizioni semplici e quelle con ripetizione? Ci sono analogie fra permutazioni e disposizioni? Scopriamo tramite gli esempi quando usare le disposizioni e le formule per calcolare il numero di disposizioni semplici e composte.

Cos’è una disposizione: definizione di disposizione
Disposizioni semplici: cosa sono e quali sono le applicazioni
Disposizioni con ripetizione: cosa sono e quali sono le applicazioni

Cos'è una disposizione
Disposizioni semplici
Disposizioni con ripetizione
Esercizi sulle disposizioni
Sfida sulle disposizioni

Cos’è una disposizione

In quanti modi puoi disporre £$k$£ elementi presi da un insieme di £$n$£ elementi? Per saperlo calcoli il numero di disposizioni!

Le disposizioni sono sequenze ordinate di £$k$£ elementi presi tra £$n$£.

Disposizioni semplici

Una disposizione è semplice quando i £$k$£ elementi di una sequenza ordinata sono diversi.

Immaginiamo di avere un sacchetto con dentro £$n$£ elementi. Ogni volta che ne pesco uno NON posso ributtarlo dentro, il sacchetto si svuota man mano che scelgo un elemento della sequenza.

La formula per calcolare il numero di disposizioni semplici di £$k$£ elementi presi da un insieme di £$n$£ elementi (e quindi £$k \le n $£) è: £$D_{n,k}=\frac{n!}{(n-k)!}=n \cdot (n-1) \cdot … \cdot (n-k+1)$£.

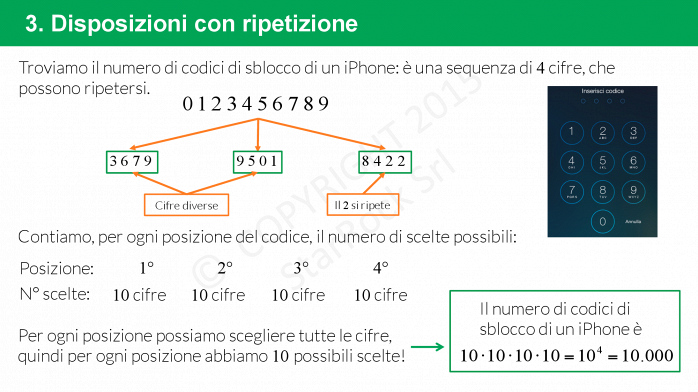
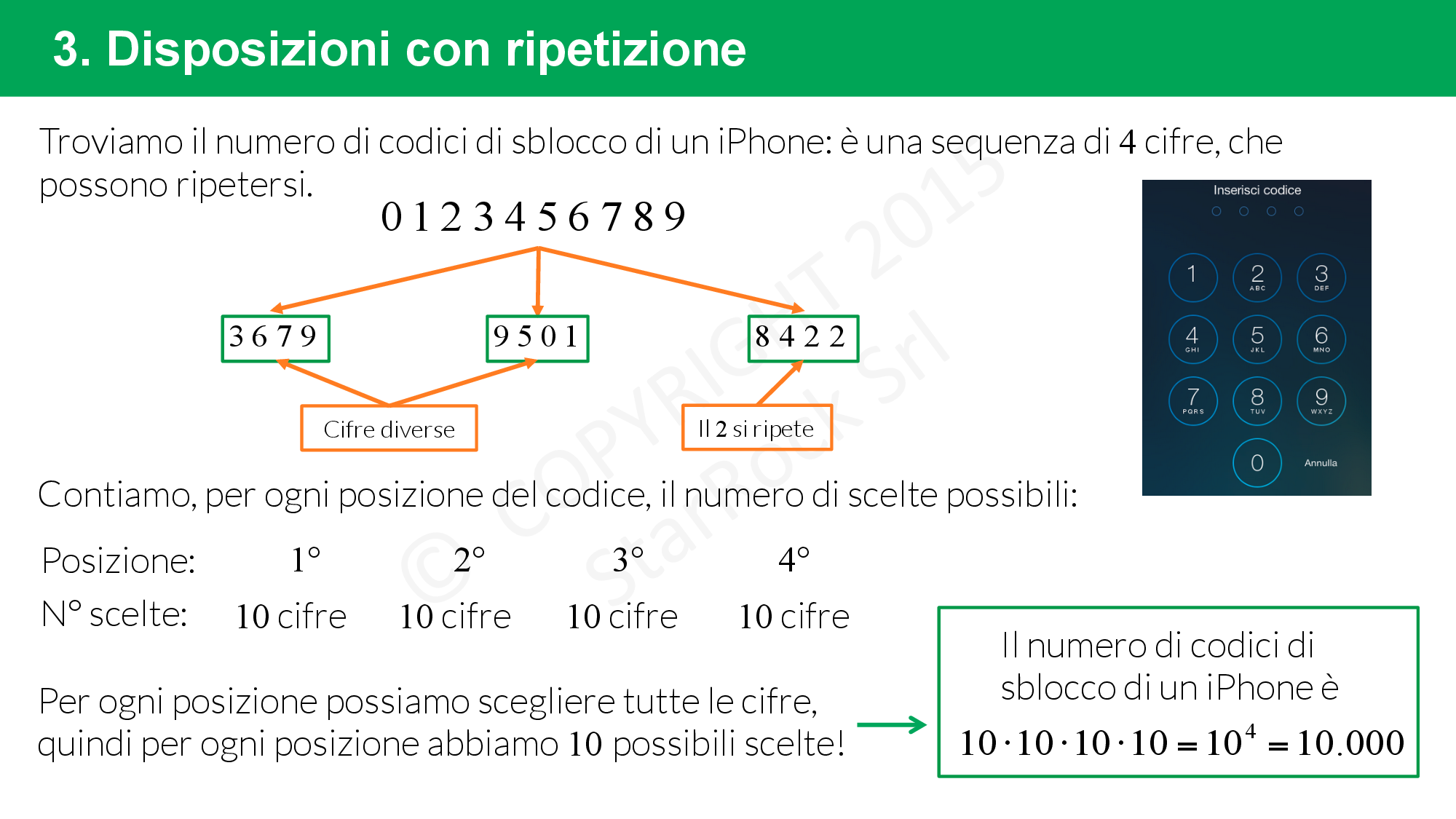
Disposizioni con ripetizione

Nelle disposizioni con ripetizione abbiamo un insieme di £$n$£ elementi totali e i £$k$£ elementi che vogliamo disporre possono ripetersi.

Immaginiamo di avere un sacchetto con dentro gli £$n$£ elementi. Ogni volta che ne pesco uno posso ributtarlo dentro. Quindi ogni volta che estraggo un elemento il sacchetto non si svuota ma ha sempre dentro gli £$n$£ elementi iniziali.

La formula per calcolare il numero di disposizioni con ripetizione è £$D’_{n,k}=n^k$£.

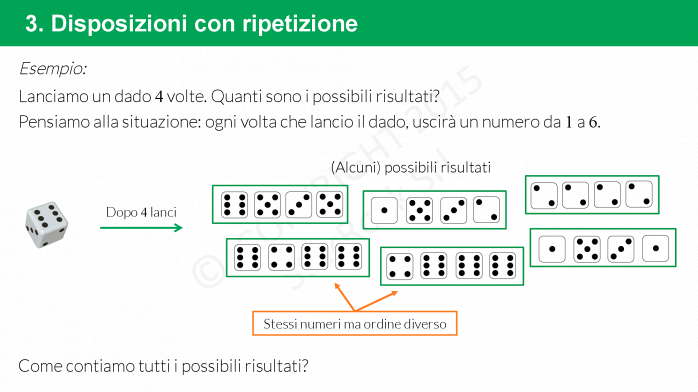
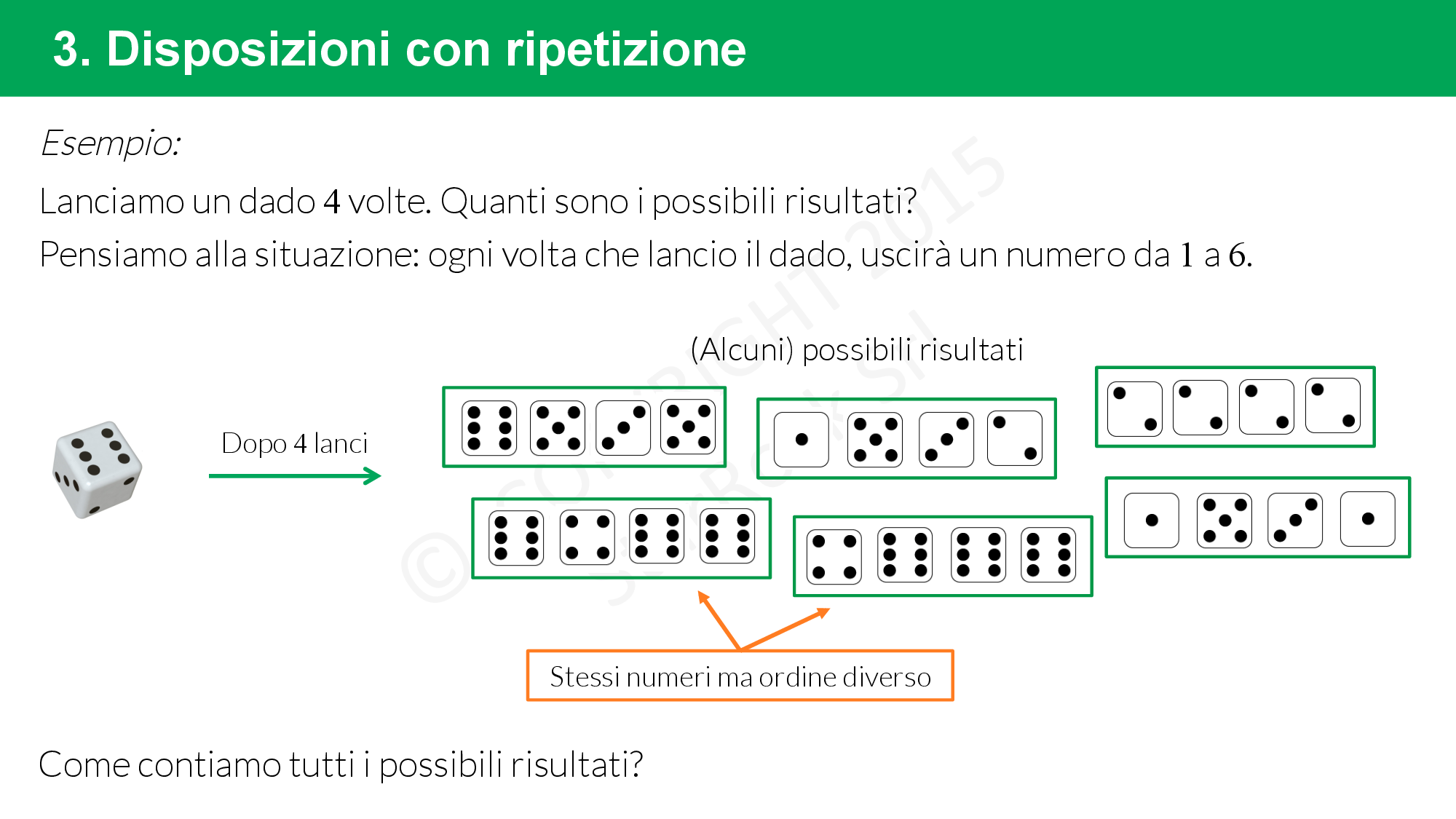
Un esempio di disposizione con ripetizione è il lancio ripetuto di un dado: se al primo lancio ho sei possibili risultati, al secondo ho sempre sei possibili risultati. Infatti se al primo lancio esce 3 può uscire anche al secondo oppure non uscire.