Rette, semirette e segmenti: cosa sono in geometria
La retta è una figura geometrica infinita che si estende in due direzioni opposte senza mai deviare o interrompersi. La sua caratteristica principale è quella di non avere né inizio né fine: è pura, priva di curvatura, e può essere pensata come la traiettoria più diretta e inalterata tra due punti nello spazio, anche se, per sua natura, non si ferma a questi punti ma continua all’infinito.
La semiretta è una figura che condivide con la retta la stessa indefettibile linearità ma, a differenza di questa, ha un inizio ben definito e si estende infinitamente in una sola direzione. È come se prendessimo una retta e decidessimo di delimitarne un estremo, dando origine a un punto di partenza da cui la semiretta si dipana verso l’infinito, senza mai curvarsi o terminare. La semiretta incorpora così l’idea di un percorso che, una volta iniziato, prosegue senza fine, delineando una traiettoria unidirezionale che si allontana sempre più dal suo punto d’origine.
Infine, il segmento si presenta come l’entità più concreta tra le tre, una porzione di retta chiaramente delimitata da due estremi. Questi punti, noti come estremi del segmento, ne definiscono la lunghezza e lo spazio occupato. A differenza delle rette e delle semirette, il segmento è finito, misurabile, e rappresenta un concetto più immediato, una distanza concreta che possiamo percepire e quantificare. Il segmento è, in un certo senso, il ponte tra l’astrazione infinita delle rette e semirette e la tangibilità del nostro mondo fisico, in cui ogni distanza ha un inizio e una fine.
Vediamoli insieme.
- Cos'è la retta
- Che cos'è un semipiano
- Cos'è la semiretta
- Cos'è il segmento
- Esercizio da svolgere: rette, semirette e segmenti
Cos’è la retta
Retta orizzontale, verticale, obliqua

Scopri le rette!
Una retta è una linea che non ha un inizio né una fine. La caratteristica principale della retta è che ha sempre la stessa direzione: è dritta, non si curva, va sempre verso lo stesso punto. Hai presente quelle strade dritte, di cui non vedi la fine? Possiamo paragonarle ad una retta!
Indichiamo le rette con una lettera minuscola dell’alfabeto: per esempio r.
Possiamo rappresentare una retta in diverse posizioni: può essere orizzontale, verticale o obliqua.
Che cos’è un semipiano
Il postulato di partizione del piano da parte di una retta dice che se disegno una retta in un piano, questa divide il piano in due regioni: “ogni segmento del piano o appartiene interamente a una delle due regioni o attraversa la retta".
Ciascuna delle due parti del piano più la retta di origine che la individua si chiama semipiano.
Il postulato dice che una qualsiasi retta di un piano divide l’insieme dei punti del piano che non le appartengono in due regioni con le seguenti proprietà:
- due punti qualsiasi appartenenti alla stessa regione £$(A; B)$£ sono gli estremi di un segmento che non interseca la retta;
- due punti qualsiasi appartenenti a regioni diverse £$(C; D)$£ sono gli estremi di un segmento che interseca la retta.
Cos’è la semiretta

Immagina di disegnare un punto su una retta: cosa succede? Il punto divide la retta in due parti che si chiamano semirette.
Una semiretta è una retta che ha un inizio, ma non ha una fine. Il punto d’inizio si chiama origine della semiretta: è il punto O che abbiamo disegnato sulla retta.
Cos’è il segmento

Disegniamo due punti su una retta: abbiamo trovato un segmento!
Un segmento è una parte di retta delimitata da due punti, detti estremi. Sono quelli che abbiamo indicato con le lettere A e B. Il segmento è limitato, ha un inizio e una fine.
Disegnando un punto £$O$£ su una retta creiamo 2 semirette opposte, che hanno come unico punto in comune £$O$£ (detto origine).
Partendo da una retta orientata (sulla quale i numeri crescono seguendo un verso) e un suo punto £$O$£, sono semirette gli insiemi formati da:
- £$O$£ e tutti i punti che lo seguono;
- £$O$£ e tutti i punti che lo precedono.
Se in una retta disegniamo 2 punti £$A$£ e £$B$£ creiamo il segmento £$AB$£ formato da £$A$£, £$B$£ (i punti estremi del segmento) e i punti compresi fra di loro.
Se gli estremi del segmento coincidono, il segmento è nullo: è un punto!
Si chiamano prolungamenti del segmento £$AB$£ le semirette:
- di origine £$A$£ che non contiene £$B$£;
- di origine £$B$£ che non contiene £$A$£.
Se su una retta disegniamo due punti £$A$£ e £$B$£, stiamo dividendo la retta in 3 parti: la semiretta di origine £$A$£ che non contiene £$B$£, il segmento £$AB$£, e la semiretta di origine £$B$£ che non contiene £$A$£.
Due segmenti sono:
- consecutivi se hanno in comune solo un estremo;
- adiacenti se sono consecutivi e in più appartengono alla stessa retta.
Esercizio da svolgere: rette, semirette e segmenti
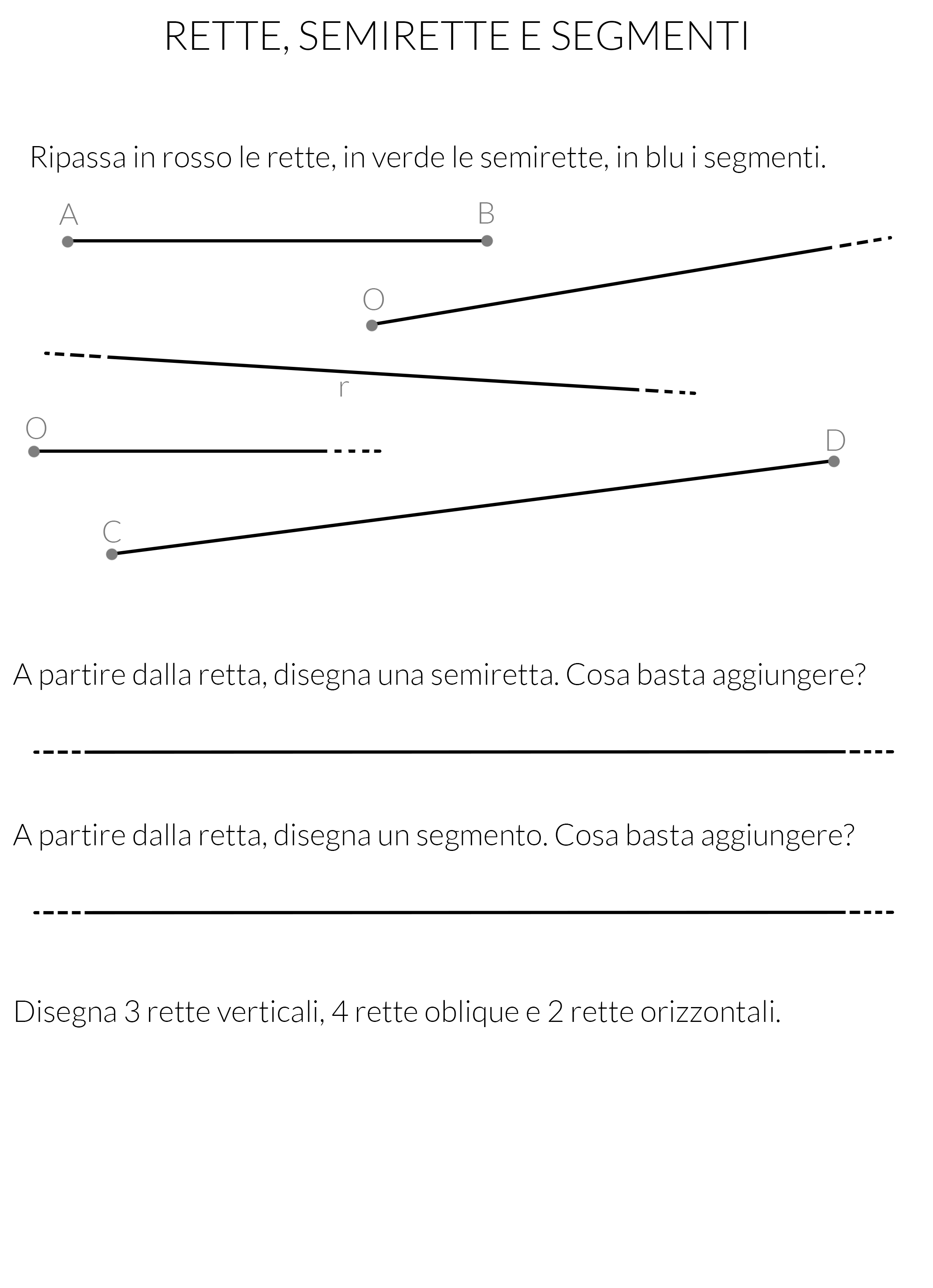
In questa lezione impariamo a riconoscere le rette, le semirette e i segmenti.
Metti alla prova gli alunni con questi semplici esercizi della scheda: .
Per prendere confidenza con le rette orizzontali, verticali e oblique, proponiamo un’attività che collega la geometria e l’arte: come dei piccoli Mondrian, ci basta un foglio e un righello. Date loro libertà di disegnare quanto credono: solo rette orizzontali e verticali, solo rette oblique, rette orizzontali, verticali e oblique tutte insieme, che si incrociano le une con le altre. Una volta disegnate tutte le linee, è il momento di colorare: utilizziamo il blu, il rosso e il giallo, cioè i colori primari come Mondrian. Realizzate un bel cartellone con tutte le opere d’arte: e pensare che è nato tutto da linee verticali, orizzontali e oblique che si incrociano su un foglio! 😉
