Come si risolvono le equazioni di primo grado

L’equazione di primo grado, spesso definita come equazione lineare, rappresenta uno degli argomenti fondamentali nell’ambito dell’aritmetica e dell’algebra. Si tratta di una relazione tra variabili, dove la più alta potenza della variabile è uno, e risolverla significa trovare il valore di questa variabile che rende vera l’equazione.

Ma cosa significa realmente risolvere un’equazione di primo grado? E come si fa? Non preoccuparti, sarà proprio quello che vedremo insieme oggi.

Innanzitutto, capiremo insieme cos’è un’equazione di primo grado, per poi andare a definire come è possibile risolverla. Vedrai che, con il tempo e un po’ di esercizio, sarà molto più semplice di quello che pensi!

• Che cos'è un'equazione di primo grado
• Come risolvere le equazioni di primo grado

Che cos’è un’equazione di primo grado

Risolvere un’equazione… Con la bilancia!

La prima equazione mai scritta

Un’identità è un’uguaglianza sempre verificata, quindi una bilancia sempre in equilibrio.

Un’equazione è, più semplicemente, un’uguaglianza tra due espressioni dove compare almeno un’incognita che indichiamo con una lettera dell’alfabeto. Il termine equazione, infatti, significa proprio uguaglianza.

Con le equazioni e il calcolo letterale, possiamo iniziare a parlare di algebra. Con l’algebra introduciamo il concetto di “sconosciuto". A differenza delle identità, l’uguaglianza in un’equazione non è sempre vera. Con le equazioni leghiamo qualcosa che non conosciamo a qualcosa che conosciamo, in modo da riuscire a trovare il valore dell’incognita.

Esempio: £$ 3x + 5 = 17 $£ è un’equazione: un’uguaglianza tra due espressioni che contiene un’incognita, la £$ x $£.

Per risolvere un’equazione, dobbiamo trovare il valore per l’incognita che rende vera l’uguaglianza, cioè che porta la bilancia ad essere in equilibrio.

Possiamo trovare un’equazione a partire da una qualsiasi espressione: prima di risolverla, non conosciamo il risultato, quindi questa è la nostra incognita!

L’obiettivo è quello di risolvere l’equazione, cioè trovare il valore dell’incognita e quindi, in questo caso, il risultato dell’espressione.

Esempio: £$ 4+ 5 – 6 $£ è una semplice espressione. Possiamo “farla diventare" un’equazione semplicemente aggiungendo l’uguale e l’incognita: £$ 4 + 5 – 6 = x $£.

Risolvere questa equazione, cioè trovare il valore della £$ x $£, equivale a risolvere la nostra espressione.

Il risultato è semplicemente £$ 3 = x $£ che possiamo leggere da sinistra verso destra o da destra verso sinistra, £$ x = 3 $£.

Trovi la tabella con tutte le formule qui.

Come risolvere le equazioni di primo grado

Come risolvere un’equazione?

Quanto vale l’incongnita?

Abbiamo studiato i monomi e i polinomi e abbiamo scoperto come riconoscere di quale grado sono.

Le equazioni sono uguaglianze tra espressioni che contengono almeno un’incognita, quindi sono ancora delle espressioni letterali, in particolare possono essere uguaglianze tra polinomi.

Possiamo capire il grado dell’equazione trovando il grado delle espressioni letterali.

Determinare il grado di un’equazione, quindi, è semplice: basta determinare il grado delle espressioni letterali che la compongono e scegliere il grado massimo.

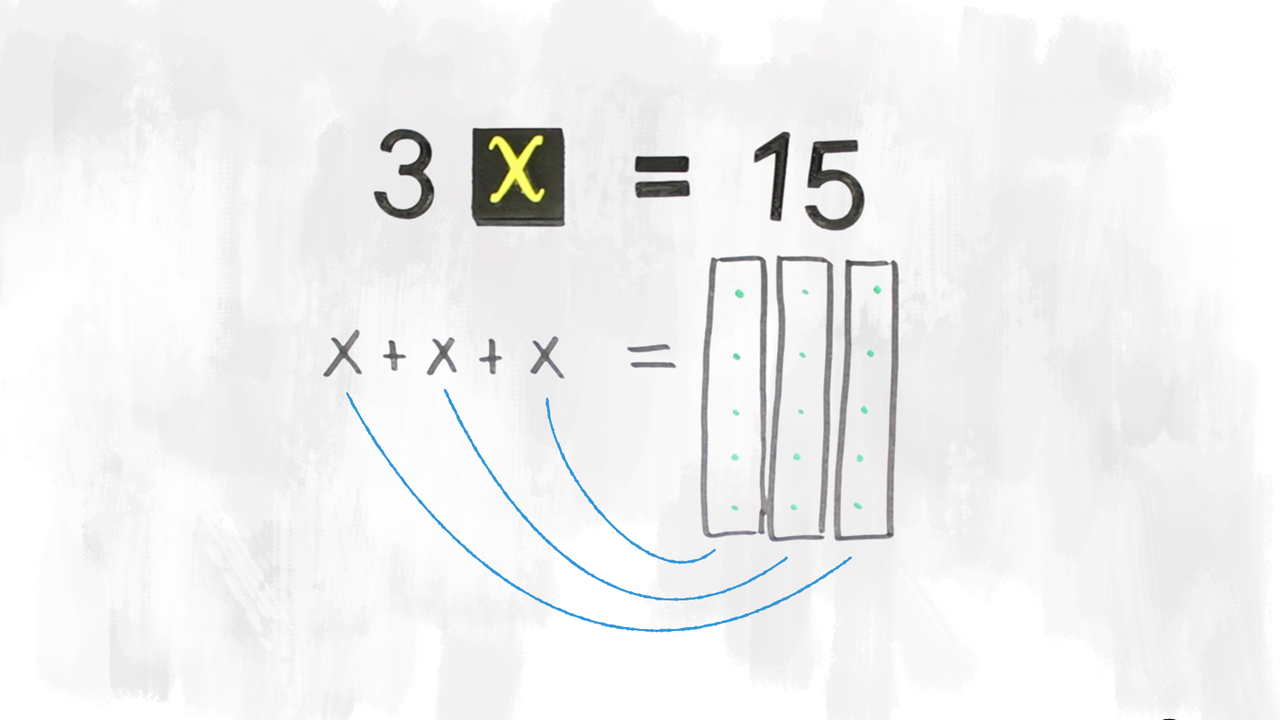
Noi andremo ad analizzare in modo più approfondito le equazioni lineari, o equazioni di primo grado, cioè quelle equazioni in cui l’incognita compare con esponente uguale a £$ 1 $£.

Un’equazione di primo grado in forma normale è un’equazione del tipo £$ ax = b $£, con £$ a \ne 0 $£. Per scrivere un’equazione in forma normale, dobbiamo separare le incognite dai termini noti: le prime a sinistra e i secondi a destra (o viceversa).

La soluzione (o radice) è £$ x = \frac{b}{a} $£.

Esempio: £$ 5 x = 15 $£ è un’equazione di primo grado in forma normale. La sua soluzione è £$ x = 3 $£.

Sono equazioni di primo grado anche queste:

• £$ 5x + 3a – 2k = 47 $£
• £$ 52b – 6 = 8 $£
• £$ \frac{6}{11} x + 4 = 2 $£