Equazioni determinate, indeterminate e impossibili

Nella matematica, specialmente nell’algebra, le equazioni possono essere classificate in base al tipo e al numero di soluzioni che possiedono. Questa classificazione ci aiuta a comprendere meglio la natura delle equazioni e il modo in cui devono essere affrontate. Vengono generalmente suddivise in tre categorie principali: determinate, indeterminate e impossibili.

Le equazioni determinate sono quelle che si risolvono con un numero finito di soluzioni; la maggior parte delle equazioni che incontriamo in matematica rientra in questa categoria. Queste equazioni sono come indovinelli che hanno una risposta precisa o un insieme limitato di risposte corrette. Risolvere un’equazione determinata significa trovare quel particolare valore o quei valori specifici che rendono vera l’equazione.

Dall’altro lato dello spettro, abbiamo le equazioni indeterminate. Queste equazioni sono interessanti perché, invece di portare a una soluzione specifica, si aprono a infinite possibilità: un’equazione indeterminata è vera per un numero illimitato di soluzioni. In un certo senso, queste equazioni ci dicono che ci sono molti modi per guardare a un problema e che molti percorsi possono portare al risultato corretto.

Infine, ci sono le equazioni impossibili. Come suggerisce il nome, queste equazioni non hanno soluzione: non importa quanto si cerchi o quali numeri si provino, non si troverà mai un valore che soddisfi l’equazione. Questo di solito accade perché l’equazione si riduce a un’affermazione contraddittoria o assurda. Le equazioni impossibili sono significative perché indicano che ci sono situazioni senza una risposta fattibile o che le condizioni poste dall’equazione non possono mai essere soddisfatte.

Scopriamole insieme!

Vuoi testare la tua preparazione? Prova il nostro quiz!

• Equazione determinata
• Equazione indeterminata
• Equazione impossibile
• Come riconoscere le equazioni determinate, indeterminate e impossibili

Equazione determinata

Un’equazione è determinata quando ammette un’unica soluzione.

Esempio: £$ \dfrac 52 x=5 $£ ha un’unica soluzione, £$ x=2 $£. È un’equazione determinata.

Trovi la tabella con tutte le formule qui.

Equazione indeterminata

Un’equazione è indeterminata se ha infinite soluzioni: qualunque valore sostituiamo al posto dell’incognita, l’uguaglianza è sempre verificata. Sono equazioni indeterminate le identità che contengono un’incognita.

Esempio: £$ 5x = 5x $£ è un’identità, quindi è sempre verificata, qualunque sia il valore di £$ x $£.

Nel risolvere un’equazione, riconosciamo che è indeterminata quando arriviamo ad avere una situazione di questo tipo: £$ 0x = 0 $£. Un numero qualsiasi moltiplicato per £$ 0 $£ dà sempre £$ 0 $£ come risultato: è un’equazione con infinite soluzioni.

Equazione impossibile

Un’equazione è impossibile se non ha nessuna soluzione. Non riusciamo a trovare un valore che, sostituito all’incognita, verifica l’uguaglianza.

Esempio: £$ 2x = 2x+3 $£ è un’equazione impossibile. Non riusciamo a trovare un numero che, sostituito all’incognita £$ x $£, renda vera questa uguaglianza.

Riconosciamo un’equazione impossibile quando ritroviamo una situazione di questo tipo: £$ 0x = 13 $£, cioè l’incognita moltiplicata per £$ 0 $£ uguale ad un numero diverso da £$ 0 $£. Sappiamo che un numero moltiplicato per £$ 0 $£ dà sempre £$ 0 $£ come risultato, quindi è impossibile trovare un numero che, moltiplicato per £$ 0 $£, dia un risultato diverso.

Come riconoscere le equazioni determinate, indeterminate e impossibili

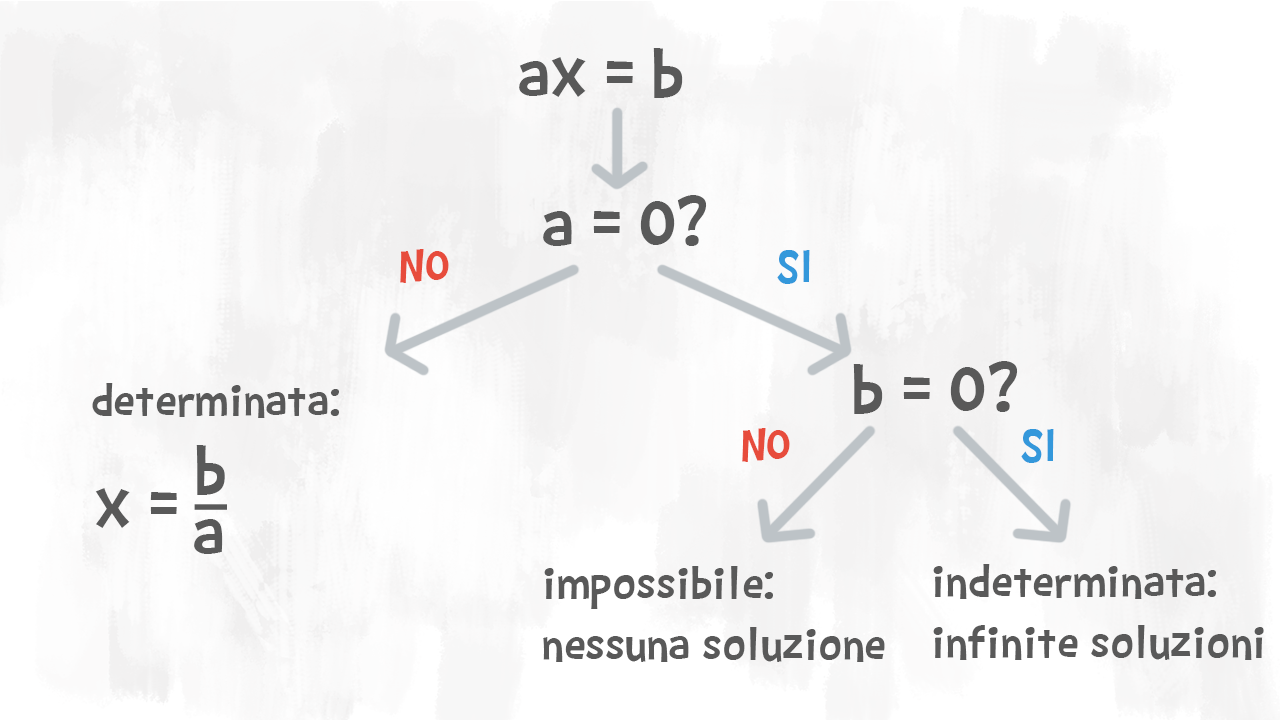
È facile riconoscere quali soluzioni ha un’equazione ridotta in forma normale. Aiutati con questo schema!

Verifica della soluzione di un’equazione

Come facciamo a capire se la soluzione che abbiamo trovato è corretta? Dobbiamo fare una verifica!

Un po’ come abbiamo già imparato a fare con la divisione: per controllare che il risultato sia corretto, moltiplichiamo il risultato per il divisore. Se otteniamo il dividendo, abbiamo svolto la divisione correttamente!

Esempio: £$ 561 : 3 = 187 $£ è una divisione corretta perché £$ 187 \cdot 3 = 561 $£

Anche per le equazioni possiamo fare una verifica per controllare se la soluzione che abbiamo trovato è corretta. Come facciamo? Basta sostituire la soluzione che abbiamo trovato al posto dell’incognita. Se otteniamo un’identità, la soluzione dell’equazione è corretta.

Esempio: £$ 2x + 1 = 7 $£ ha soluzione £$ x = 3 $£. Controlliamo se è corretta sostituendo il £$ 3 $£ al posto della £$ x $£.
£$ 2 \cdot 3 + 1 = 7 \\ 6 + 1 = 7 \\ 7 = 7 $£
Abbiamo trovato un’identità, quindi £$ x = 3 $£ è proprio soluzione dell’equazione.