Le potenze: cosa sono e come si calcolano
Le potenze sono formate da due numeri: una base e un esponente. Ci permettono di scrivere in modo compatto delle moltiplicazioni ripetute. Immagina di dover moltiplicare un numero per se stesso tante volte. Grazie alle potenze puoi scrivere questa moltiplicazione in maniera più compatta.
Invece di scrivere £$ 3 \cdot 3 \cdot 3 \cdot 3 $£ puoi scrivere £$ 3^4 $£! La base della potenza è il numero che si ripete nella moltiplicazione, l’esponente della potenza invece indica quante volte la base si ripete.
Sono molto utili e ci aiutano a non sprecare tempo: scopri con noi cosa sono, come possiamo definirle e come si calcolano!
Ripassa la definizione di potenza, divertiti con basi ed esponenti e impara le proprietà delle potenze che permettono di velocizzare i calcoli quando devi moltiplicare o dividere due potenze che hanno la stessa base.
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- L'invenzione degli scacchi: l'inizio delle potenze
- Cosa sono le potenze
- Come calcolare la potenza di un numero
- Come calcolare la potenza di una lettera
- Le potenze e le loro proprietà
- Potenze di 0 e di 1
- Potenze con esponente 0 oppure 1
- Le potenze di 10
- Esercizi da svolgere sulle potenze
- Interrogazione sulle potenze e le loro proprietà
- Potenze: ecco la sfida!
L’invenzione degli scacchi: l’inizio delle potenze
L’inventore degli scacchi offrì al suo re il gioco in cambio di una ricompensa: un chicco di riso per la prima casella della scacchiera, due per la seconda, quattro per la terza e così via… fino all’ultima casella!
Secondo te, il re è riuscito a soddisfare questa richiesta?
Cosa sono le potenze
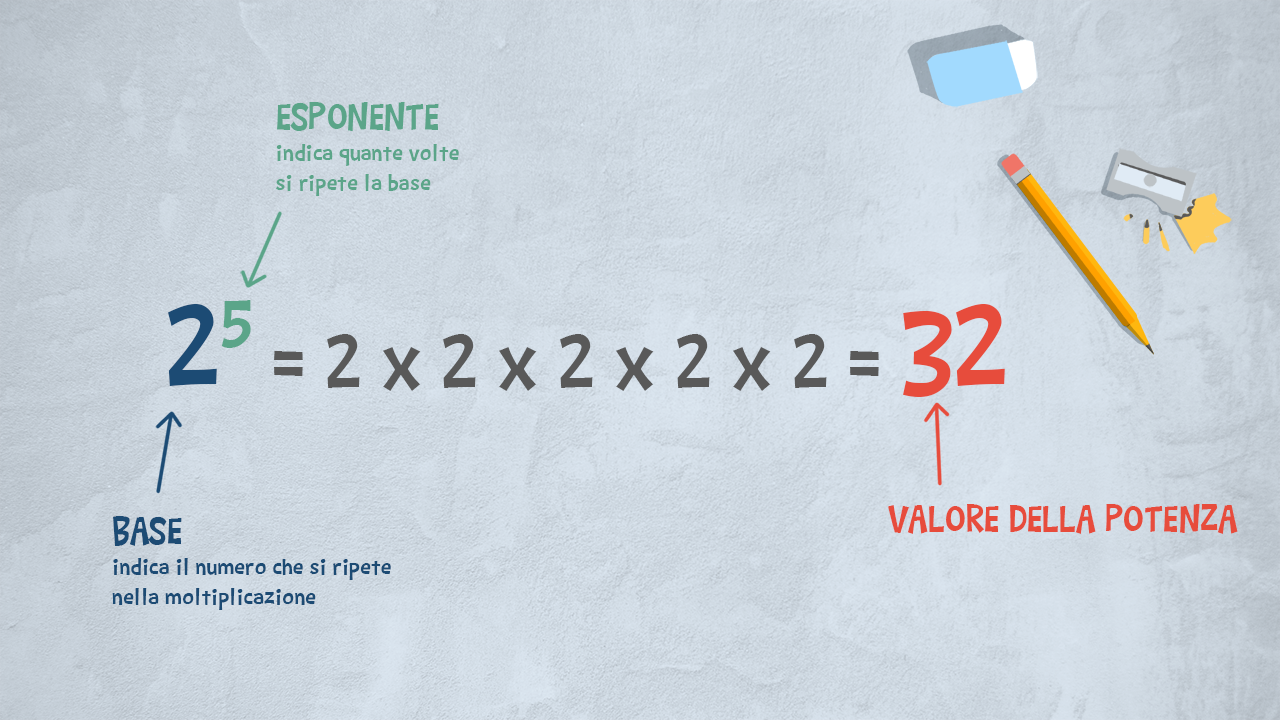
Abbiamo studiato che le moltiplicazioni sono un modo di scrivere le addizioni in cui gli addendi sono uguali e si ripetono più volte:
2 + 2 + 2 + 2 + 2 = 2 x 5 lo stesso addendo, il 2, sommato a se stesso per 5 volte.
Esiste un modo per scrivere una moltiplicazione dove i fattori si ripetono uguali più volte? Certo che esiste! Si chiama elevamento a potenza.
2 x 2 x 2 x 2 x 2 = 2£$^5$£ lo stesso fattore, il 2, moltiplicato per se stesso 5 volte: questa è una potenza!
Una potenza è formata da due elementi:
- la base, che indica il numero che si ripete;
- l’esponente, che indica per quante volte si ripete la base.
Scriviamo 2£$^5$£ e leggiamo “due elevato a cinque", oppure “due alla quinta".
Come calcolare la potenza di un numero
Le potenze sono un modo veloce per scrivere le moltiplicazioni. Un prodotto in cui i fattori sono tutti uguali si può scrivere sotto forma di potenza. L’esponente indica quante volte la base si ripete nella moltiplicazione.
Esempio: £$ 6^3 $£ è una potenza. Il £$ 6 $£ è la base e il £$ 3 $£ è l’esponente. Scrivere £$ 6^3 $£ equivale a scrivere £$ 6 \cdot 6 \cdot 6 $£.
Come calcolare la potenza di una lettera
Le potenze funzionano anche con le lettere: se moltiplichiamo per se stesso un numero qualsiasi £$ a $£ per £$ n $£ volte, possiamo scrivere la potenza £$ a^n $£.
Le potenze e le loro proprietà
L’elevamento a potenza in N permette di scrivere un prodotto di fattori tutti uguali in modo più compatto. Per esempio £$ 2 \cdot 2 \cdot 2 = 2^3 $£, il £$ 2 $£ è la base, il £$ 3 $£ è l’esponente, che indica il numero di volte che moltiplichiamo la base per se stessa.
Anche le potenze come le quattro operazioni hanno delle proprietà:
- il prodotto di potenze con la stessa base è uguale ad una potenza che ha ancora la stessa base e come esponente la somma degli esponenti: £$ 3^4 \cdot 3^2 = 3^6 $£
- il quoziente di potenze con la stessa base è uguale ad una potenza che ha ancora la stessa base e come esponente la differenza tra gli esponenti: £$ 3^4 : 3^2 = 3^2 $£
- il prodotto di potenze con lo stesso esponente è uguale ad una potenza che ha ancora lo stesso esponente e come base il prodotto delle basi: £$ 9^4 \cdot 3^4 = 27^4 $£
- il quoziente di potenze con lo stesso esponente è uguale ad una potenza che ha ancora lo stesso esponente e come base il quoziente delle basi: £$ 9^4 : 3^4 = 3^4 $£
- la potenza di una potenza è una potenza della stessa base che ha per esponente il prodotto degli esponenti: £$ (3^4)^2 = 3^8 $£
Calcola il prodotto di potenze con la stessa base
Il prodotto di due potenze con la stessa base è uguale ad una potenza che ha:
- la stessa base e
- per esponente la somma degli esponenti.
Per moltiplicare due potenze con la stessa base, basta sommare i due esponenti.
Il risultato è uguale alla base moltiplicata per se stessa tante volte quante la somma degli esponenti!
Esempio: £$ 5^2 \cdot 5^3 $£ il risultato è ancora una potenza £$ 5^{2 + 3} = 5^5 $£
Infatti: £$ 5^2 \cdot 5^3 = (5 \cdot 5) \cdot ( 5 \cdot 5 \cdot 5) =$£ £$ 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 = 5^5 $£
Calcola il quoziente di potenze con la stessa base
Il quoziente di due potenze con la stessa base è uguale ad una potenza che ha:
- la stessa base e
- per esponente la differenza tra gli esponenti.
Per dividere due potenze con la stessa base, basta sottrarre i due esponenti.
Il risultato è uguale alla base moltiplicata per se stessa tante volte quante la differenza tra gli esponenti!
Esempio: il risultato di £$ 4^6 : 4^2 $£ è ancora una potenza £$ 4^{6 – 2} = 4^4 $£
Potenze di 0 e di 1
Abbiamo studiato con le moltiplicazioni che esistono due fattori anomali, lo 0 e l’1. Anche per le potenze questi due numeri si comportano in modo particolare.
Una potenza che ha come base 1, è sempre uguale a 1: infatti sappiamo che l’1 è l’elemento neutro della moltiplicazione, quindi 1£$^3$£ = 1 x 1 x 1 = 1. Non importa quanto sia grande l’esponente, la potenza è sempre uguale a 1.
Una potenza che ha come base 0, è sempre uguale a 0: sappiamo che lo 0 è l’elemento assorbente della moltiplicazione, quindi 0£$^4$£ = 0 x 0 x 0 x 0 = 0. Non importa quanto sia grande l’esponente, la potenza è sempre uguale a 0.
Potenze con esponente 0 oppure 1
Spostiamoci adesso all’esponente: cosa succede se lo 0 oppure l’1 sono all’esponente?
Un numero elevato a 1 resta quel numero. Pensa a cos’è l’esponente: indica quante volte si ripete un fattore. Se è uguale a 1, vuol dire che prendiamo la base e la ripetiamo una sola volta: 4£$^1$£ = 4.
L’esponente uguale a 0, invece, è un po’ birichino: qualsiasi numero (escluso lo 0) elevato alla 0, dà come risultato 1, per esempio 8£$^0$£ = 1.
Le potenze di 10
Calcolare le potenze con base 10 è semplicissimo: basta aggiungere dopo l’1 tanti zeri quanti indicati dall’esponente.
10£$^1$£ = 10
10£$^2$£ = 100
10£$^3$£ = 1000
…
Sono quelle che hai già incontrato nella scrittura dei polinomi numerici per scomporre i numeri molto grandi.
Esercizi da svolgere sulle potenze

Come funzionano le potenze? Ecco una scheda per scoprirlo al meglio!
Scaricala qui:

Pronto per la verifica di matematica sulle potenze? Allenati con questi esercizi! Cerca di trovare il risultato da solo e poi controlla le soluzioni per verificare il tuo lavoro. Vedrai che il compito in classe sarà un gioco da ragazzi!
Scarica qui il pdf con gli esercizi:
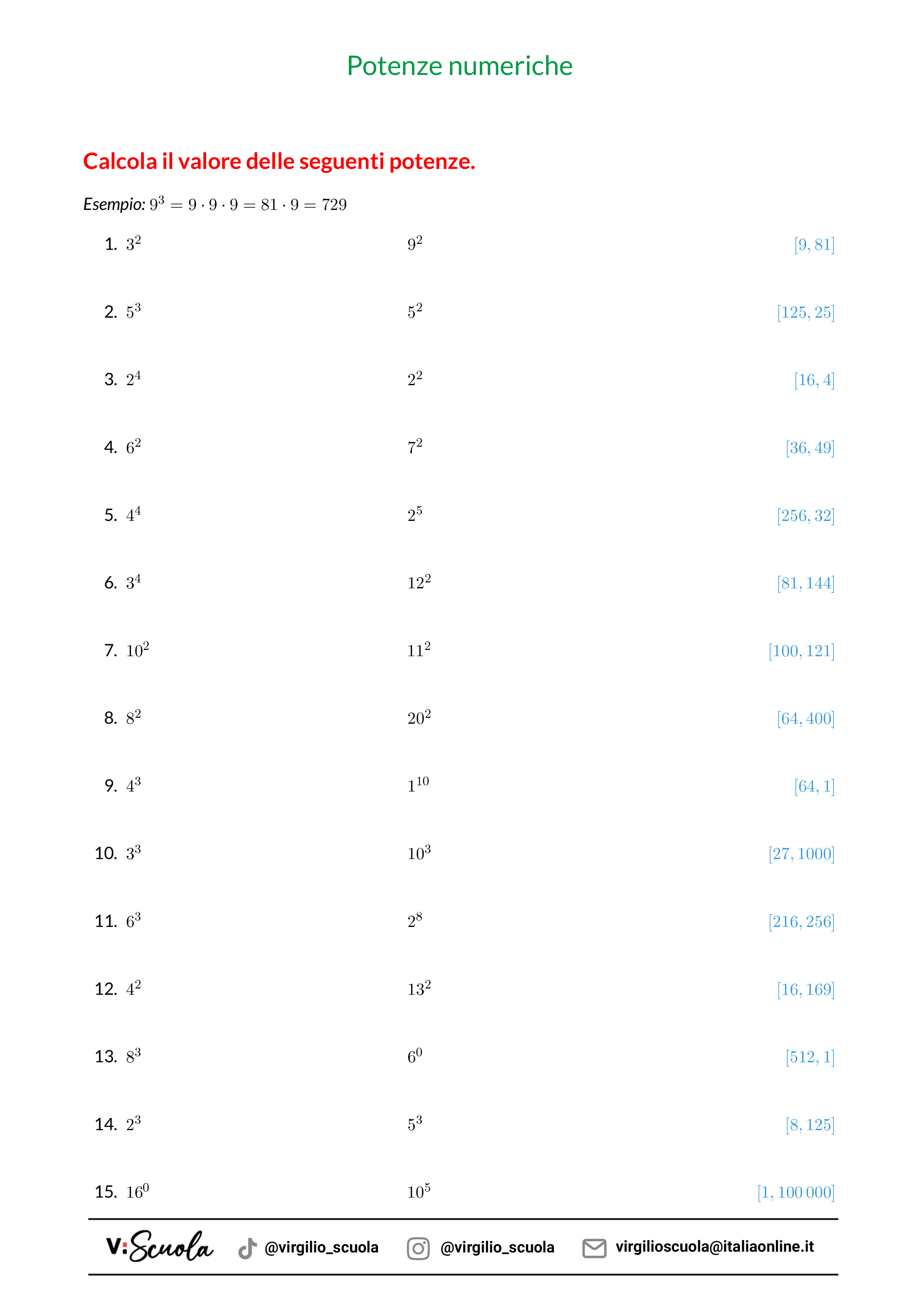
Preoccupato per la verifica sulle potenze? Che ne dici di esercitarti calcolando il valore di alcune semplici potenze numeriche? Metticela tutta e guarda le soluzioni solo per controllare di aver fatto bene il tuo lavoro.
Scarica qui il pdf degli esercizi:
Mappa concettuale sulle potenze
Consulta, scarica e stampa la mappa mentale delle potenze. Ripassa il nome dei termini e non dimenticare mai come funzionano le potenze di 0 e di 1!

Scarica qui la mappa mentale:
Interrogazione sulle potenze e le loro proprietà
Ora che sai tutto delle potenze dei numeri naturali, scopri quali possono essere le domande che ti può fare il prof all’interrogazione! Ti ricordi cosa sono le potenze e le loro proprietà? Se hai dei dubbi, ripassa con i video! Se invece vuoi altri esercizi, allenati subito con i tre livelli così sarai una potenza nelle potenze!
Potenze: ecco la sfida!
Sfida:
Soluzione:
È tempo di paghetta! Ma cosa c’entrano le potenze? Se vuoi avere una paghetta più alta, ti conviene imparare a confrontare le potenze dei numeri naturali. Prova a risolvere la sfida: prima di controllare la soluzione, guarda i video della lezione con gli esempi e allenati con gli esercizi spiegati sulle potenze e le loro proprietà!
