Numeri primi e numeri composti: definizione

I numeri primi sono quei numeri maggiori di 1 che hanno esattamente due divisori: 1 e se stessi. Questi numeri formano la base su cui si costruisce la teoria dei numeri, trovando impiego in campi moderni come la crittografia e l’analisi algoritmica.

Dall’altra parte dello spettro troviamo i numeri composti, quelli che possono essere divisi in fattori più piccoli. Questi numeri rappresentano l’altra faccia della medaglia nella classificazione dei numeri interi e sono fondamentali per comprendere la struttura e la distribuzione dei numeri primi stessi.

Non a caso, i numeri composti possono essere scomposti in fattori primi: si identificano quali sono i numeri primi che, moltiplicati tra loro, danno come risultato un numero composto.

Scopriamo insieme come fare!

A cosa servono i numeri primi

A cosa servono i numeri primi? Pensiamo al digitale terrestre, ai sistemi di pagamento elettronico, al biglietto aereo… In tutte queste cose interviene la crittografia, che significa “scrittura nascosta".

La crittografia studia i metodi per rendere il significato di un messaggio incomprensibile a persone non autorizzate a leggerlo. I numeri primi permettono di “cifrare", cioè camuffare un messaggio e poi di decifrarlo, cioè di ritrovarne il significato nascosto!

Per questo continuiamo a scoprirne sempre di più grandi: più grandi sono, più sono misteriosi e incomprensibili!

È stato istituito un premio per chi riesce a scoprire un numero primo: 3000 dollari, ma si può arrivare fino a 50 mila se si scopre un numero primo con 100 milioni di cifre! Ti è venuta voglia di scoprire un numero primo?

I numeri primi e i numeri composti: definizione

Un semplice trucco per riconoscerli

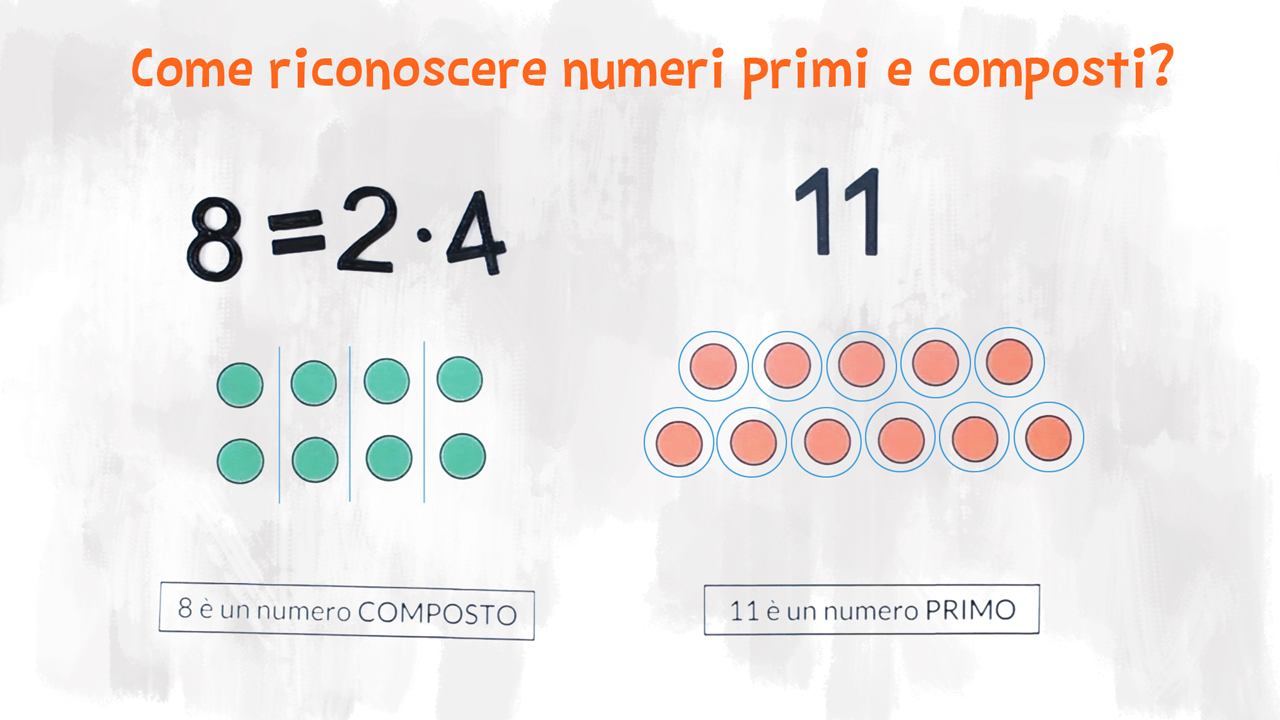
Un numero primo è un numero maggiore di 1 divisibile solo per 1 e per se stesso. Quindi un numero primo è un numero che ha esattamente due divisori.

• 2 è un numero primo: è divisibile solo per 1 e per 2;
• 5 è un numero primo: è divisibile solo per 1 e per 5;
• 17 è un numero primo: è divisibile solo per 1 e per 17;
• …

Ci sono infiniti numeri primi! Lo aveva dimostrato già Euclide nel suo libro Elementi, la più importante opera di matematica che conosciamo, scritto tra il IV e il III secolo a.C.. Ma non tutti i numeri sono primi. Abbiamo parlato di numeri con più divisori diversi oltre all’1 e a loro stessi.

I numeri composti sono quei numeri che hanno più di due divisori.

Esempio: il 6 è un numero composto perché ha come divisori 1 e 6, ma anche 2 e 3. In tutto ha quattro divisori!

I numeri primi sono il fondamento della matematica: il teorema fondamentale dell’aritmetica assicura che ogni numero naturale, o è primo, o si può scrivere come prodotto di numeri primi in modo unico. Quindi tra tutti gli infiniti numeri che conosciamo, possiamo riconoscere numeri primi e numeri che sono prodotto di primi!

Come riconoscere un numero primo

Finché ci troviamo davanti numeri relativamente piccoli, non è difficile capire se si tratta di un numero primo o di un numero composto. Cosa succede se i numeri diventano più grandi? Come facciamo ad individuare i divisori di quel numero, o a capire che non ha nessun divisore?

Per individuare i numeri primi, è utile il crivello di Eratostene. È un antico procedimento per il calcolo dei numeri primi a partire dalla tavola dei numeri.

Possiamo individuare tutti i numeri primi procedendo per passi:

• evidenziamo il numero 2, poi cancelliamo tutti i suoi multipli.
• Facciamo lo stesso con il numero 3, il numero 5 e il numero 7.
• Ad ogni passo evidenziamo il più piccolo fra i numeri, è sicuramente un numero primo (se non lo fosse, sarebbe divisibile per numero primo più piccolo e quindi sarebbe stato cancellato in uno dei passi precedenti). Cancellando poi i suoi multipli più grandi, eliminiamo dall’elenco i numeri composti.

Altrimenti possiamo procedere per tentativi: dividiamo un numero per i primi 2, 3, 5, 7, …. Se troviamo un quoziente esatto, il nostro numero di partenza non è primo, altrimenti andiamo avanti e continuiamo a ricercare divisori tra tutti i numeri primi minori o uguali alla metà del nostro numero. Se non ne troviamo neanche uno che dà un quoziente esatto, abbiamo trovato un numero primo!

Tavola dei numeri primi da 1 a 1000

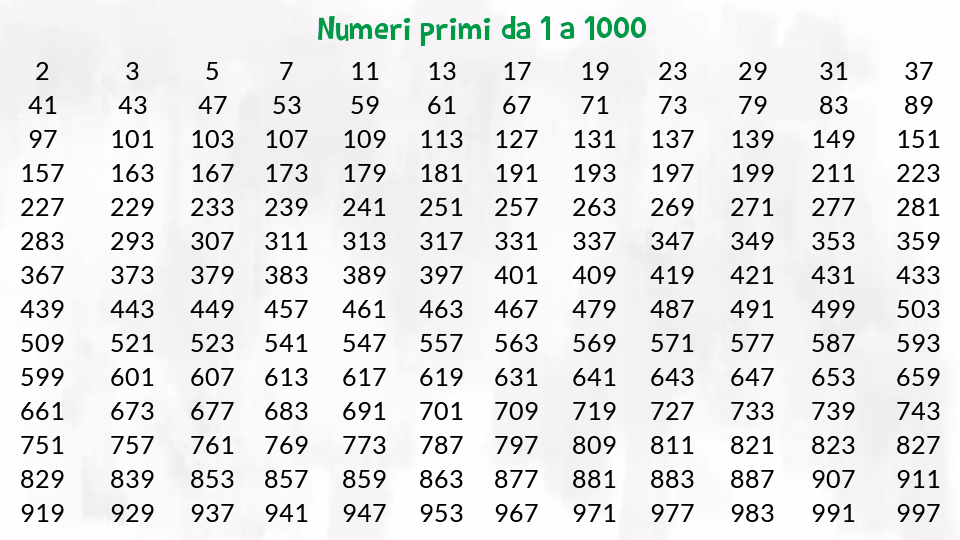
Scarica la tavola dei numeri primi da 1 a 1000: .

Scarica PDF

La fattorizzazione in numeri primi

Un numero £$ a $£ è divisore di un altro numero £$ n $£ se £$ n $£ è multiplo di £$ a $£. Cosa vuol dire multiplo? Se £$ n $£ è il doppio di £$ a $£, per esempio, possiamo scrivere £$ n = 2 \cdot a $£. Ogni numero può essere fattorizzato, cioè scritto come prodotto dei suoi divisori.
I numeri primi hanno solo due divisori, l’£$ 1 $£ e loro stessi.

Attraverso la fattorizzazione in numeri primi, possiamo scrivere tutti i numeri come prodotto di numeri primi.

Esempio: £$ 12 = 2 \cdot 2 \cdot 3 \\ 45 = 3 \cdot 3 \cdot 5 $£

Curiosità sui numeri primi

Da questa lezione abbiamo imparato molto sui numeri primi… Ma qual è il “primo numero primo"?

Lo 0 è un numero primo? Abbiamo visto che lo 0 è multiplo di tutti i numeri. Qualsiasi numero moltiplicato per 0, dà come risultato ancora 0. Sicuramente 0 non è un numero primo.

Che cosa possiamo dire del numero 1? Anche l’1 non è un numero primo: un numero primo è divisibile per 1 e per se stesso, invece il numero 1 è divisibile solo per se stesso. Non ha due divisori come tutti i numeri primi, ma ne ha uno soltanto: quindi il numero 1 non è un numero primo. E non è neanche un numero composto, avendo un solo divisore: per esserlo, dovrebbe averne più di due!

Il primo numero primo è il 2.

Il 2 è anche l’unico numero primo pari. Tutti gli altri numeri primi sono dispari!

I numeri primi gemelli sono numeri primi consecutivi, cioè separati solo da un numero: per esempio 11 e 13 sono primi gemelli, ma anche 29 e 31, oppure 101 e 103. Nel libro “La solitudine dei numeri primi" si fa un accenno ai numeri primi gemelli: i due protagonisti hanno molte cose in comune, ma non riescono mai a trovarsi perché divisi da un ostacolo insormontabile, un po’ come due primi gemelli che arrivano ad essere molto vicini, ma non riescono mai a toccarsi perché c’è sempre un numero pari ad ostacolarli.

Il più grande numero primo conosciuto ha più di 22 milioni di cifre.