I criteri di congruenza e di similitudine dei triangoli
Il triangolo, una delle figure geometriche più semplici e allo stesso tempo affascinanti, è stato oggetto di studio e di ammirazione per generazioni di matematici e geometri. Due dei concetti più importanti associati ai triangoli sono la congruenza e la similitudine, eppure, spesso, sono fonte di confusione per molti. Ma cosa significano esattamente questi termini e come possono essere utilizzati per studiare e confrontare diversi triangoli?
Quando parliamo di “congruenza“, ci riferiamo a triangoli che sono essenzialmente identici in forma e dimensione. Immagina di ritagliare un triangolo da un pezzo di carta e di sovrapporlo perfettamente a un altro: se combaciano esattamente, sono congruenti. Questo significa che hanno lati della stessa lunghezza e angoli della stessa ampiezza.
La “similitudine“, invece, si riferisce a triangoli che condividono la stessa forma ma possono avere dimensioni diverse. Due triangoli simili hanno angoli uguali, ma i loro lati sono proporzionali piuttosto che identici in lunghezza. Potresti pensare a un modello di triangolo e alla sua versione ridimensionata: differenti in dimensione, ma simili nella forma.
In questo articolo, cercheremo di chiarire questi concetti e di descrivere quali sono i tre criteri di congruenza e i tre criteri di similitudine dei triangoli!
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Tabelle sui criteri di congruenza e similitudine
- Cos'è la congruenza tra triangoli
- Primo criterio di congruenza dei triangoli
- Secondo criterio di congruenza dei triangoli
- Terzo criterio di congruenza dei triangoli
- Ripassa per l'interrogazione sui criteri di congruenza
- Primo criterio di similitudine dei triangoli
- Secondo criterio di similitudine dei triangoli
- Terzo criterio di similitudine dei triangoli
Tabelle sui criteri di congruenza e similitudine
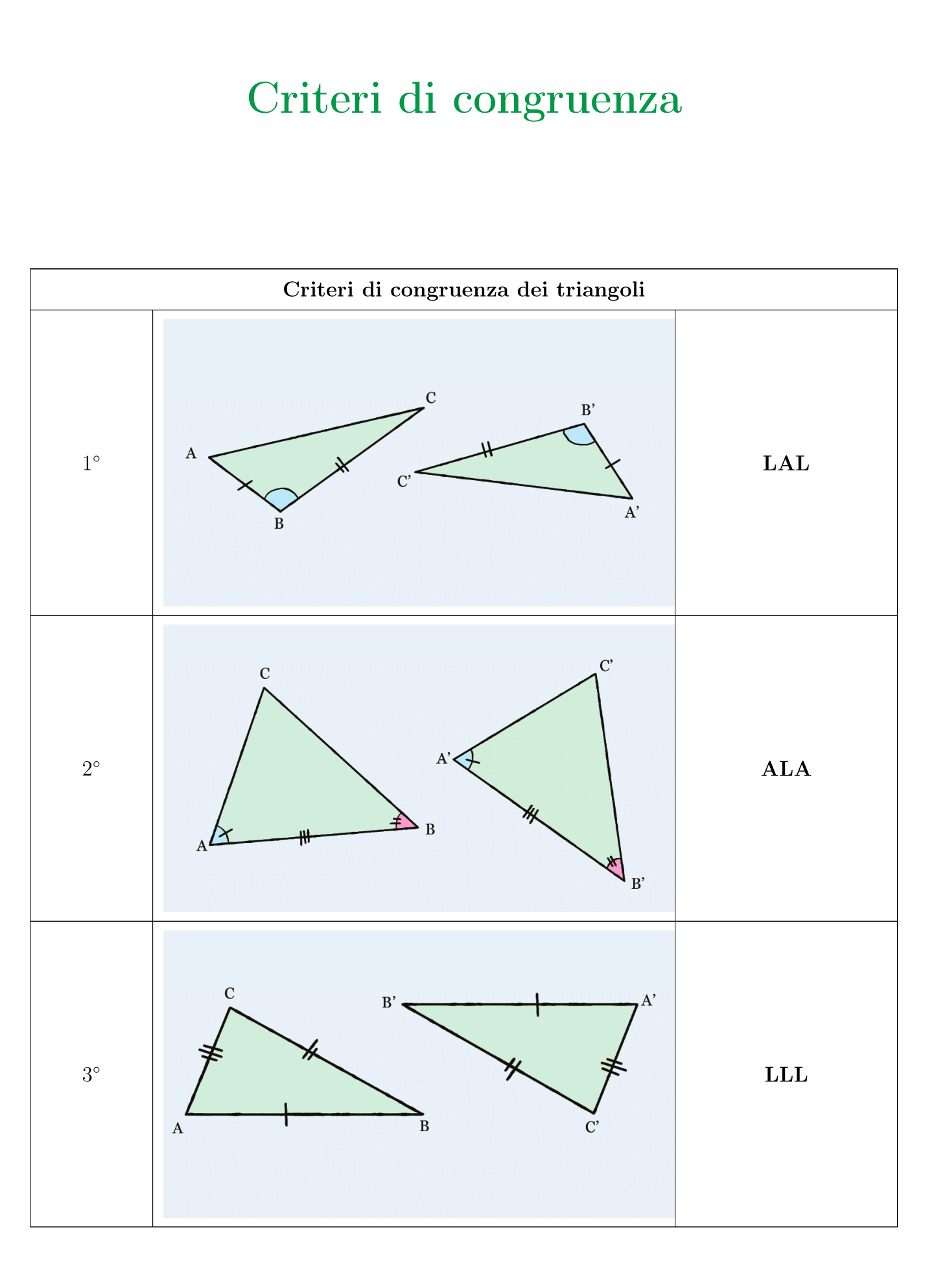
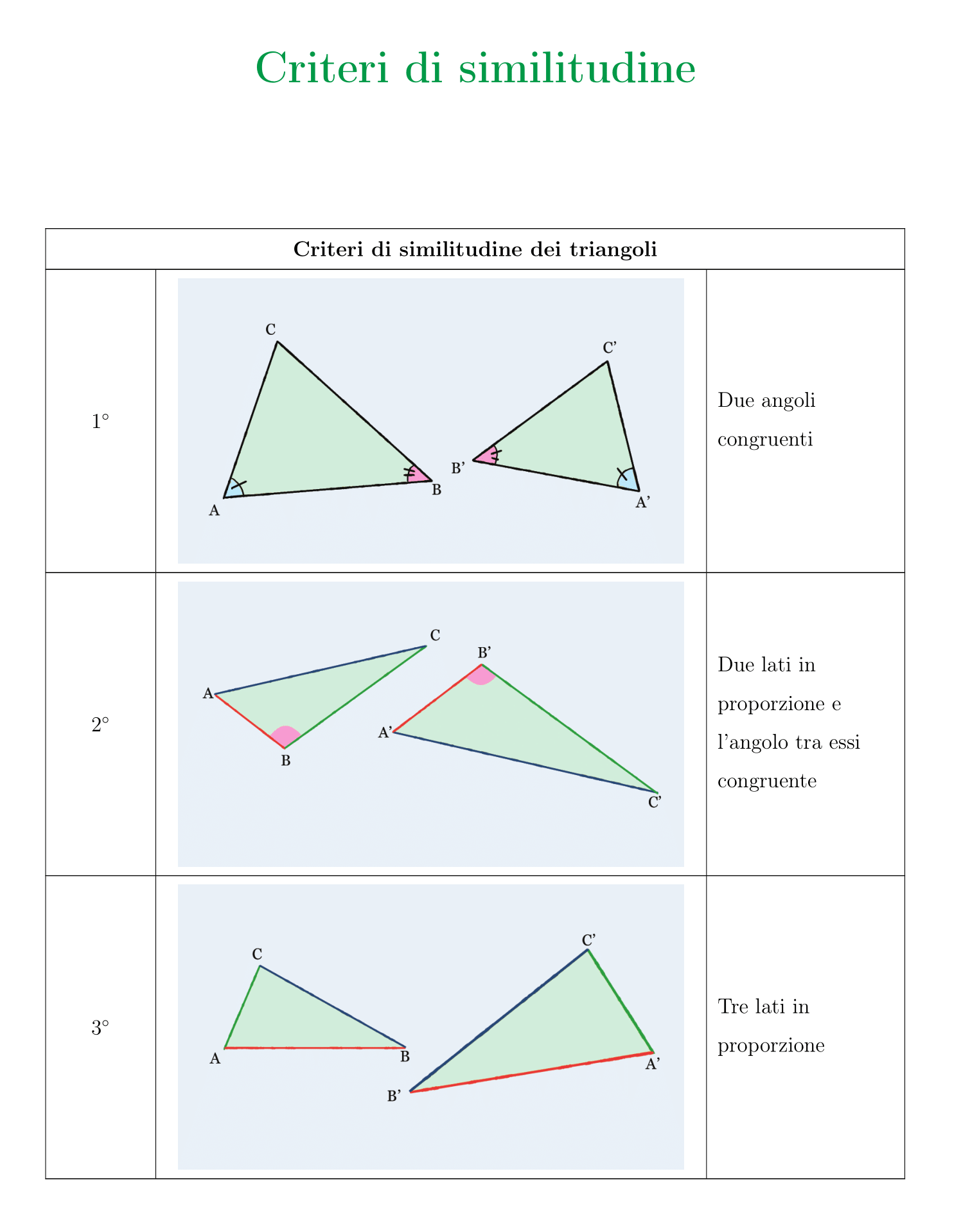
Questo schema riassuntivo ti sarà utile per cercare di ripassare i criteri di similitudine e di congruenza dei triangoli: stampalo e portalo sempre con te!
Cos’è la congruenza tra triangoli

Hai già visto quando due segmenti sono congruenti: quando si sovrappongono perfettamente e la loro lunghezza è la stessa.
Come facciamo invece a riconoscere due triangoli congruenti? Anche in questo caso possiamo dire che due triangoli sono congruenti quando sono perfettamente sovrapponibili, punto per punto.
In due triangoli congruenti, lati corrispondenti e angoli corrispondenti sono congruenti: quindi hanno la stessa misura!
Nella figura i lati £$ AB $£, £$ A’B’$£ e £$A’’B’’$£ sono lati corrispondenti in triangoli congruenti. Allora sono congruenti!
£$ AB\cong A’B’\cong A’’B’’ $£
Ma se fisicamente non possiamo o non riusciamo a verificare che due triangoli sono sovrapponibili, come possiamo stabilire se sono congruenti? Per fortuna esistono i criteri di congruenza dei triangoli! Se riesci a verificare le ipotesi di almeno un criterio di congruenza, allora puoi concludere che due triangoli sono congruenti.
Primo criterio di congruenza dei triangoli
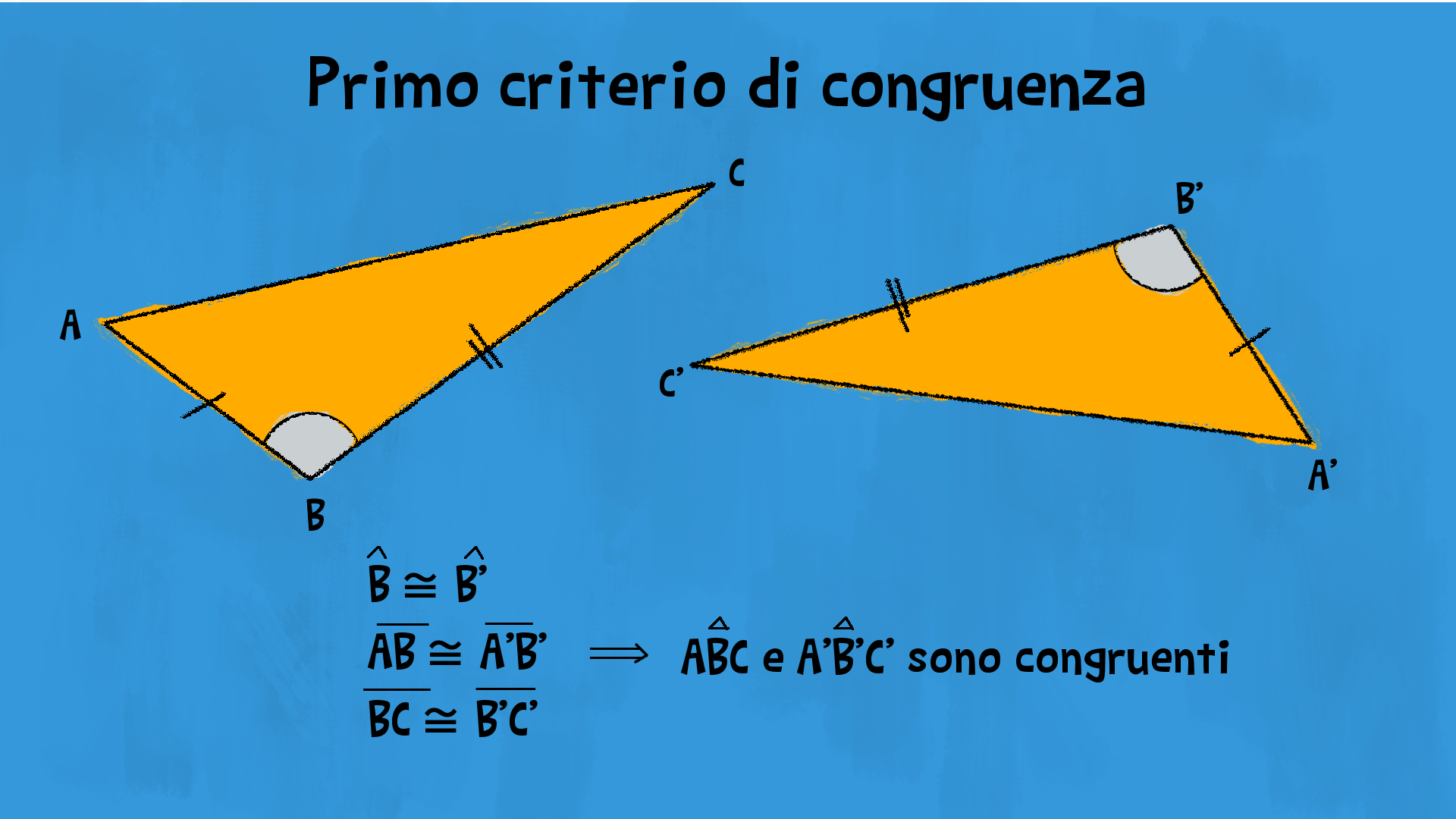
Due triangoli sono congruenti quando hanno rispettivamente congruenti due lati e l’angolo tra essi compreso.
Ipotesi
£$\overline{AB}=\overline{A’B’}$£ £$\overline{CA}=\overline{C’A’}$£ £$B\widehat{A}C=B’\widehat{A’}C’$£
Tesi
£$ \stackrel{\triangle}{ABC}\, \cong\,\stackrel{\triangle}{A’B’C’}$£
Possiamo riassumere il primo criterio di congruenza con la sigla LAL: Lato, Angolo, Lato.
Secondo criterio di congruenza dei triangoli
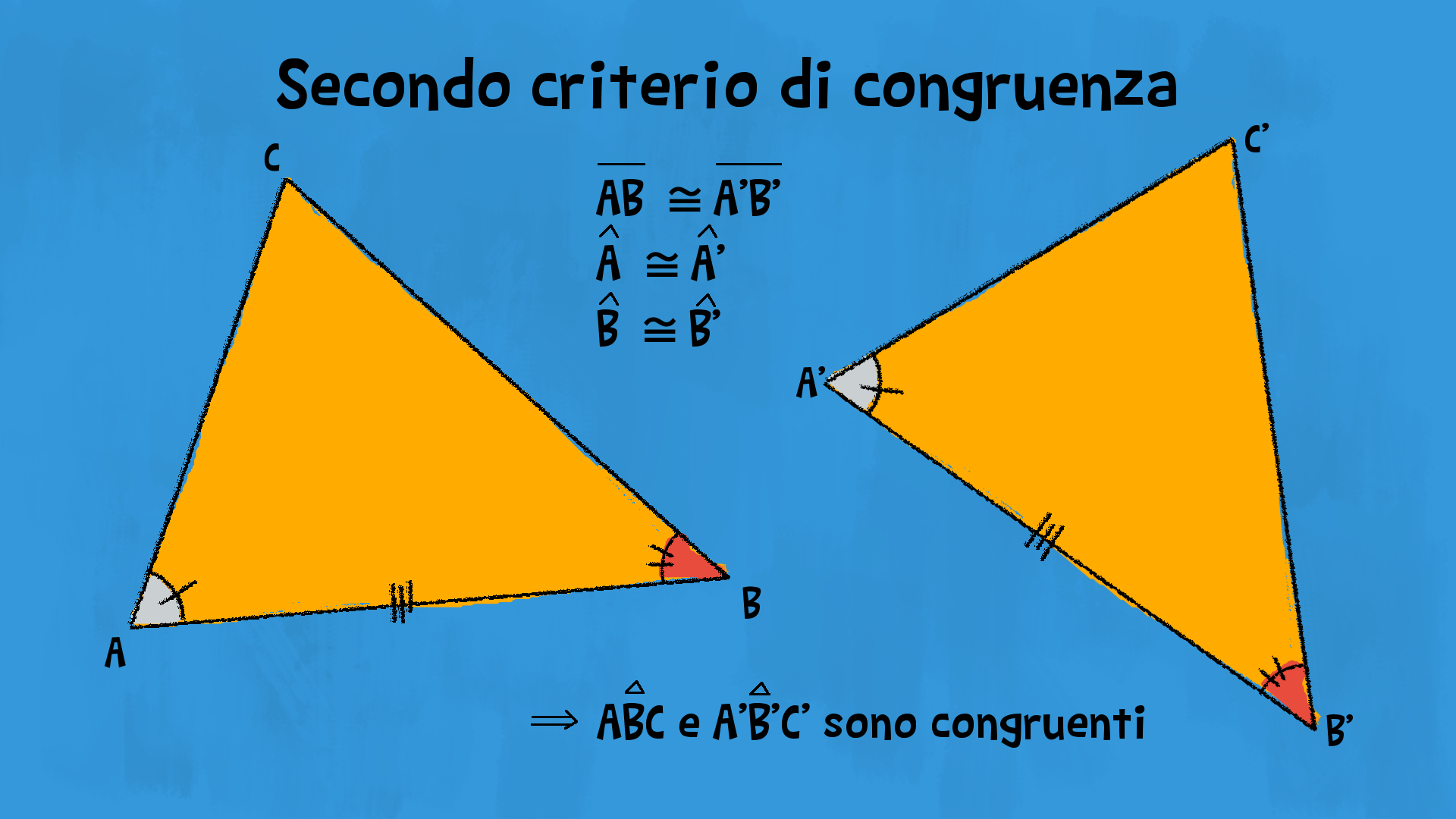
Due triangoli sono congruenti quando hanno rispettivamente congruenti due angoli e il lato tra essi compreso.
Ipotesi
£$ \overline{AB}=\overline{A’B’} $£
£$ C\widehat{A}B\cong C’\widehat{A’}B’ $£
£$ A\widehat{B}C \cong A’\widehat{B’}C’ $£
Tesi
£$ \stackrel{\triangle}{ABC}\, \cong\,\stackrel{\triangle}{A’B’C’}$£
Possiamo riassumere il secondo criterio di congruenza con la sigla ALA: Angolo, Lato, Angolo.
Terzo criterio di congruenza dei triangoli
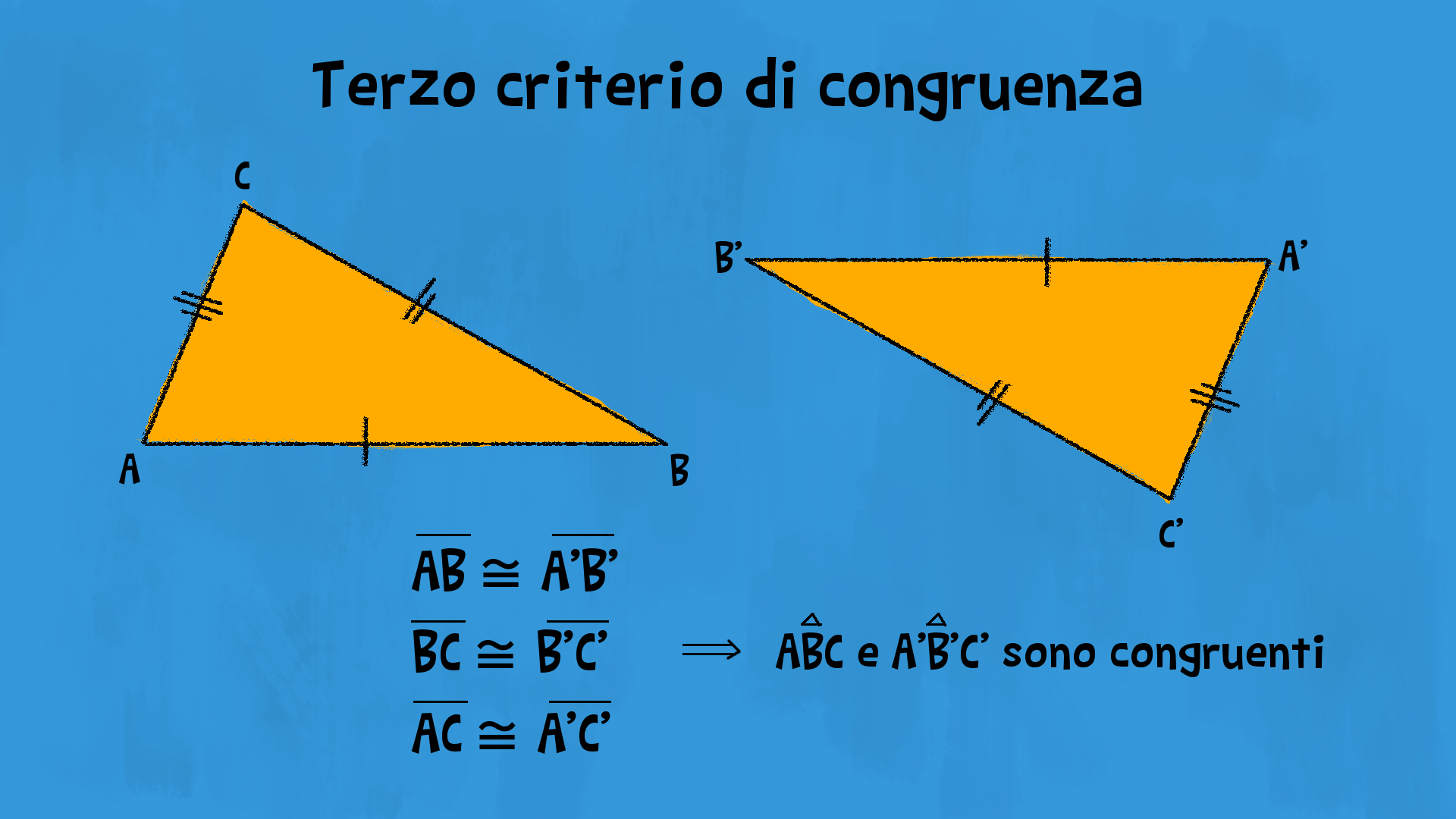
Due triangoli sono congruenti quando hanno rispettivamente congruenti tutti e tre i lati.
Ipotesi
£$ \overline{AB}=\overline{A’B’} $£
£$ \overline{BC}=\overline{B’C’} $£
£$ \overline{CA}=\overline{C’A’} $£
Tesi
£$ \stackrel{\triangle}{ABC}\, \cong\,\stackrel{\triangle}{A’B’C’}$£
Possiamo riassumere il terzo criterio di congruenza con la sigla LLL: Lato, Lato, Lato.
Ripassa per l’interrogazione sui criteri di congruenza
Cosa dicono i tre criteri di congruenza? Sai applicarli in un esercizio? Prova a rispondere alle domande della nostra interrogazione!
Prova anche la nostra sfida!
Soluzione
Spugna sta tagliando dalla stoffa le vele di riserva per le scialuppe. Ha misurato due lati e l’angolo tra di essi. La vela sarà identica all’originale? Scopri come usare i criteri di congruenza dei triangoli per aiutare Spugna!
Primo criterio di similitudine dei triangoli

Due triangoli sono simili se hanno due coppie di angoli corrispondenti congruenti.
Ipotesi
£$\widehat{A} \cong \widehat{A’}$£ £$\widehat{B}\cong\widehat{B’}$£
Tesi
£$A \stackrel \triangle{B} C$£ e £$A’ \stackrel \triangle{B’} C’$£ sono simili
Secondo criterio di similitudine dei triangoli
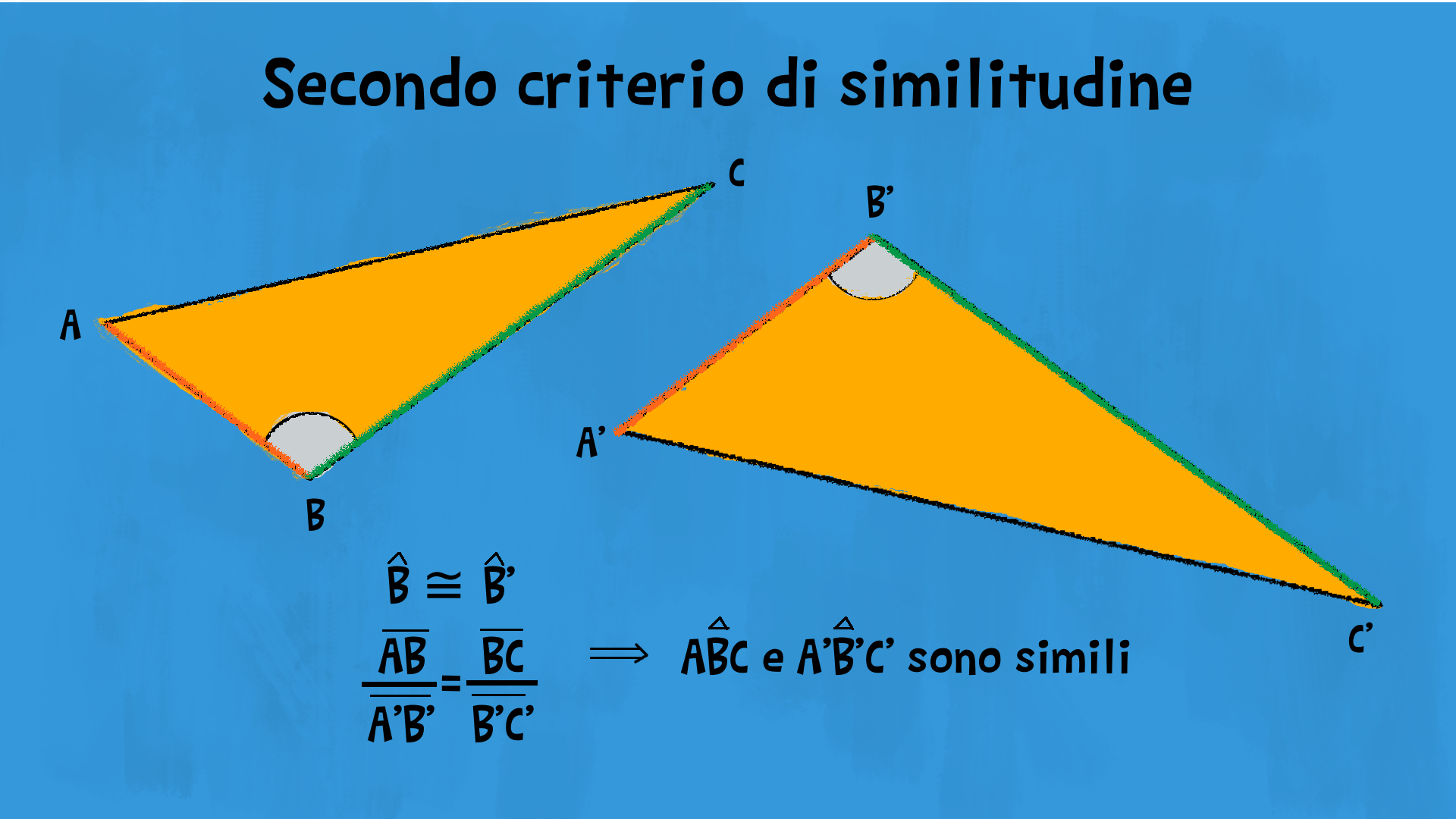
Due triangoli sono simili se hanno due coppie di lati corrispondenti proporzionali e gli angoli compresi congruenti.
Ipotesi
£$\dfrac{\overline{AB}}{\overline{A’B’}}=\dfrac{\overline{BC}}{\overline{B’C’}}$£ £$\widehat{B}\cong\widehat{B’}$£
Tesi
£$A \stackrel \triangle{B} C$£ e £$A’ \stackrel \triangle{B’} C’$£ sono simili
Terzo criterio di similitudine dei triangoli

Due triangoli sono simili se hanno tre coppie di lati corrispondenti proporzionali.
Ipotesi
£$\dfrac{\overline{AB}}{\overline{A’B’}}=\dfrac{\overline{BC}}{\overline{B’C’}}=\dfrac{\overline{AC}}{\overline{A’C’}}$£
Tesi
£$A \stackrel \triangle{B} C$£ e £$A’ \stackrel \triangle{B’} C’$£ sono simili
