Il teorema di Pitagora: enunciato, dimostrazione e formule
Il teorema di Pitagora è il più conosciuto fra i teoremi di matematica. Questa formula stabilisce una relazione profonda tra i lati di un triangolo rettangolo ed ha radici che affondano in una storia molto antica. Ma chi era realmente Pitagora? E come si è arrivati alla scoperta di un teorema che porta il suo nome e che è diventato un pilastro della geometria?
La storia del Teorema di Pitagora ci porta indietro nel tempo, attraversando civiltà e culture, da quella greca antica alle rive del fiume Indo. Mentre il teorema prende il nome dal filosofo e matematico greco Pitagora, esistono indicazioni che concetti simili potrebbero essere stati conosciuti in altre civiltà molto prima della sua epoca, come la civiltà babilonese e cinese. Ma cosa afferma esattamente questo teorema? E come si può provare che sia universalmente vero per ogni triangolo rettangolo?
Lo scopriremo in questo articolo: vedremo insieme come è nato questo teorema, qual è il suo enunciato e come è stato dimostrato.
- La storia della nascita del teorema di Pitagora
- L'enunciato del teorema di Pitagora
- Le formule dirette e inverse del teorema di Pitagora
- Quando usare il teorema di Pitagora
- La dimostrazione di Euclide del teorema di Pitagora
- Il teorema di Pitagora secondo i Babilonesi e i Cinesi
La storia della nascita del teorema di Pitagora
C’è una leggenda sulla nascita del teorema di Pitagora.
Secondo una delle narrazioni più popolari, Pitagora, durante uno dei suoi viaggi in Egitto, venne introdotto ai misteri della geometria dai sacerdoti locali. Un giorno, mentre aspettava di essere ricevuto da Policrate, osservando attentamente le piastrelle di un pavimento, ebbe un’illuminazione. Notò che, disegnando un quadrato su ciascuno dei tre lati di un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa (il lato più lungo) era esattamente uguale alla somma delle aree dei quadrati costruiti sugli altri due lati. Eureka!
Questa scoperta lo portò a formulare il teorema che ora porta il suo nome. La leggenda racconta che, euforico per la sua scoperta, Pitagora offrì in sacrificio cento buoi agli dei. Sebbene non ci siano prove storiche concrete di questa particolare narrazione, ciò che è certo è che il Teorema di Pitagora ha avuto un impatto duraturo sulla matematica e sul modo in cui comprendiamo la geometria e che, comunque, ancora oggi questa scoperta porta il suo nome.

L’enunciato del teorema di Pitagora
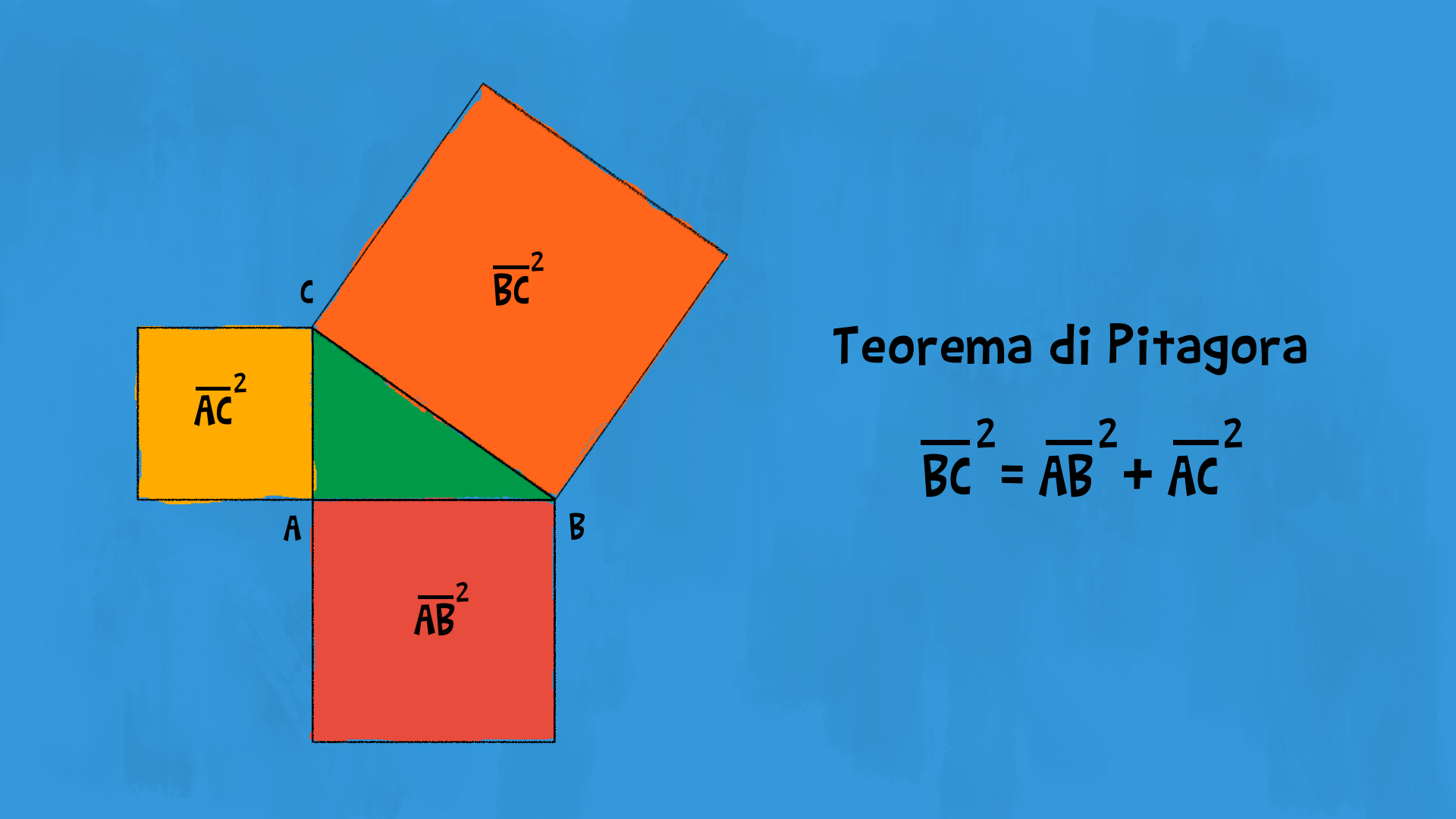
Il teorema di Pitagora è valido per tutti i triangoli rettangoli. Ti ricordi come sono fatti i triangoli rettangoli? Sono tutti quei triangoli che hanno un angolo retto. I due lati adiacenti all’angolo retto sono i cateti, cateto maggiore (che indicheremo con £$ \text{cateto}_1 $£) e cateto minore (che indicheremo con £$ \text{cateto}_2 $£), il terzo lato, opposto all’angolo retto, è l’ipotenusa. L’ipotenusa è sempre il lato più lungo di un triangolo rettangolo.
In ogni triangolo rettangolo il quadrato dell’ipotenusa è equivalente alla somma dei quadrati dei due cateti.
Cosa vuol dire questo enunciato? Se calcoliamo l’area del quadrato che ha per lato l’ipotenusa, vediamo che è uguale alla somma delle aree dei quadrati che hanno per lato il cateto maggiore e il cateto minore del triangolo rettangolo.
Aiutandoci con la matematica, possiamo scrivere il teorema di Pitagora così:
$$ \text{ipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 $$
Le formule dirette e inverse del teorema di Pitagora
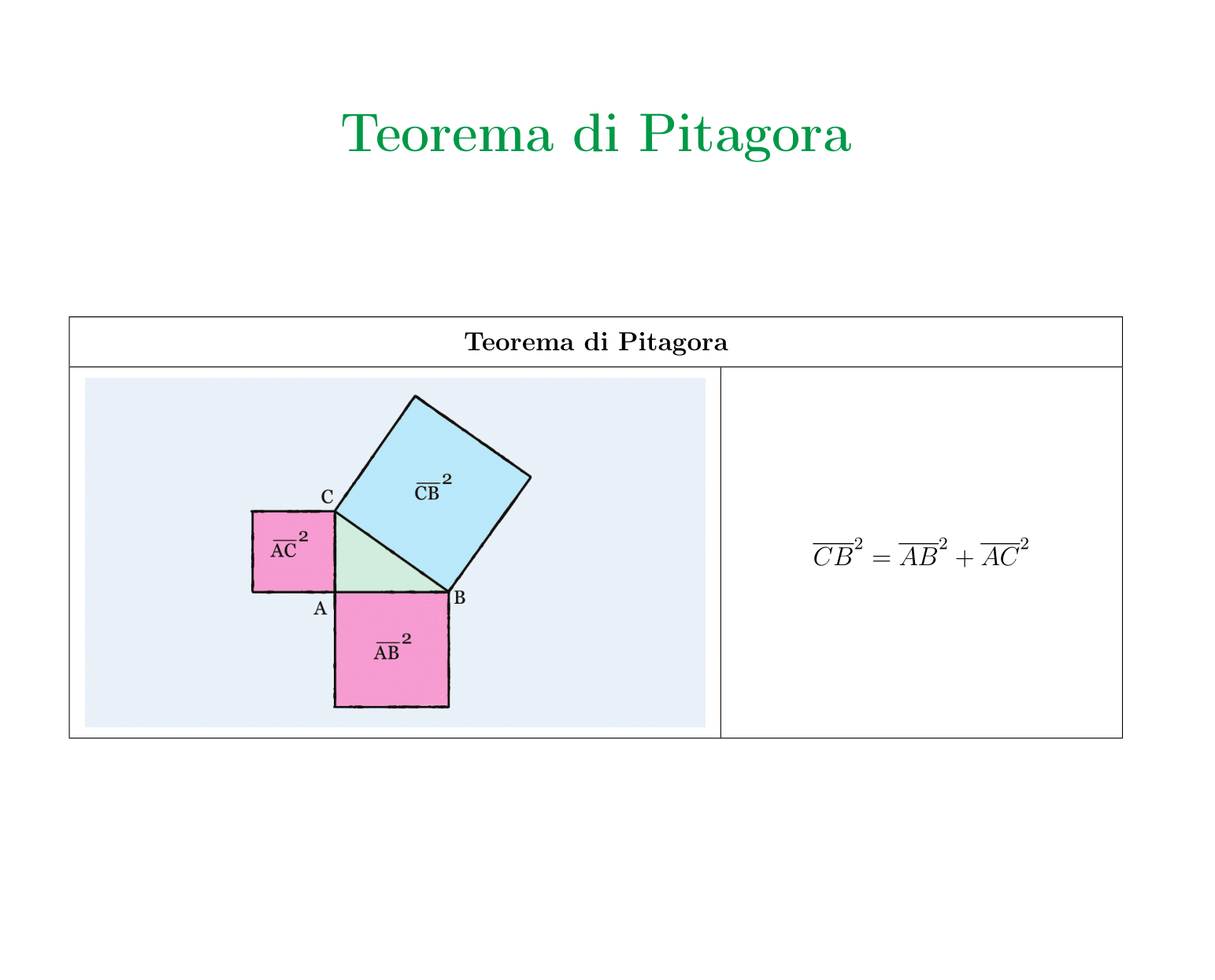
Il teorema di Pitagora mette in relazione i lati di un triangolo rettangolo.
In un triangolo rettangolo la somma dei quadrati costruiti sui cateti, è equivalente al quadrato costruito sull’ipotenusa.
$$i^2 = c_1^2 + c_2^2$$ $$\overline{BC}^2=\overline{AB}^2+\overline{AC}^2 $$
Le formule inverse, invece, sono:
$$c_1^2=i^2-{c_2}^2$$ $$\overline{AB}^2=\overline {BC}^2-\overline{AC}^2$$ $$c_2^2=i^2-c_1^2$$ $$\overline{AC}^2=\overline{BC}^2-\overline{AB}^2$$
Se ti aiuta sapere cosa stai cercando, prova a dare un’occhiata a queste formule:
- per trovare l’ipotenusa £$AB=\sqrt{AC^2+BC^2}$£;
- per trovare il cateto minore £$AC=\sqrt{AB^2-BC^2}$£;
- per trovare il cateto maggiore £$BC=\sqrt{AB^2-AC^2}$£.
Quando usare il teorema di Pitagora
Se £$ABC$£ è un triangolo rettangolo, £$AB$£ e £$AC$£ sono i cateti e £$BC$£ l’ipotenusa, allora £$\overline{BC}^2=\overline{AB}^2+\overline{AC}^2$£.
Estraendo la radice quadrata e usando le formule inverse puoi trovare:
- la misura dell’ipotenusa conoscendo i cateti: £$\overline{BC}=\sqrt{\overline{AB}^2+\overline{AC}^2}$£;
- la misura di un cateto conoscendo l’ipotenusa e l’altro cateto £$\overline{AB}=\sqrt{\overline{BC}^2-\overline{AC}^2}$£
Questo teorema vale solo per i triangoli rettangoli ed è uno dei teoremi più utili non solo per le Invalsi, ma anche per risolvere ogni problema di geometria: con il teorema di Pitagora puoi calcolare anche la lunghezza di un segmento nel piano cartesiano. Puoi sfruttarlo per risolvere problemi di congruenza o similitudine dei triangoli. Può essere utile per calcolare il perimetro di figure complesse che si possono scomporre in triangoli rettangoli!
La dimostrazione di Euclide del teorema di Pitagora
Il teorema di Pitagora è forse la più antica dimostrazione documentata di matematica.
La dimostrazione rigorosa che studiamo solitamente a scuola è quella di Euclide, dal primo libro degli Elementi. Pitagora riuscì a fornire una dimostrazione visiva, mentre Euclide ha dimostrato più concretamente il teorema, raccogliendo il lavoro di Pitagora e aggiungendo delle dimostrazioni matematiche alle sue intuizioni.
La sua dimostrazione si basa sull’uso di figure geometriche. Immaginate un triangolo rettangolo con i lati £$a, b, c$£ (dove c è l’ipotenusa). Euclide iniziò disegnando un quadrato con il lato lungo £$c$£ e piazzando quattro copie del triangolo rettangolo all’interno di questo quadrato in modo che formassero un quadrato più piccolo al centro.
L’area del grande quadrato (di lato £$c$£) è, naturalmente, £$c^2$£. L’area combinata dei quattro triangoli è £$ab$£, e l’area del piccolo quadrato al centro è £$(a-b)^2$£. Euclide ha mostrato che queste due aree combinate (l’area dei quattro triangoli più l’area del quadrato centrale) sono uguali all’area del grande quadrato. Questo dimostra che £$a^2-b^2=c^2$£.
Il genio di questa dimostrazione risiede nella sua semplicità visiva. Senza fare ricorso a complesse formule o calcoli, Euclide ha utilizzato le proprietà fondamentali della geometria per dimostrare un concetto che è diventato una pietra miliare della matematica. La sua dimostrazione è un esempio brillante di come la pura logica e la creatività possano lavorare insieme per rivelare verità universali.
Il teorema di Pitagora secondo i Babilonesi e i Cinesi
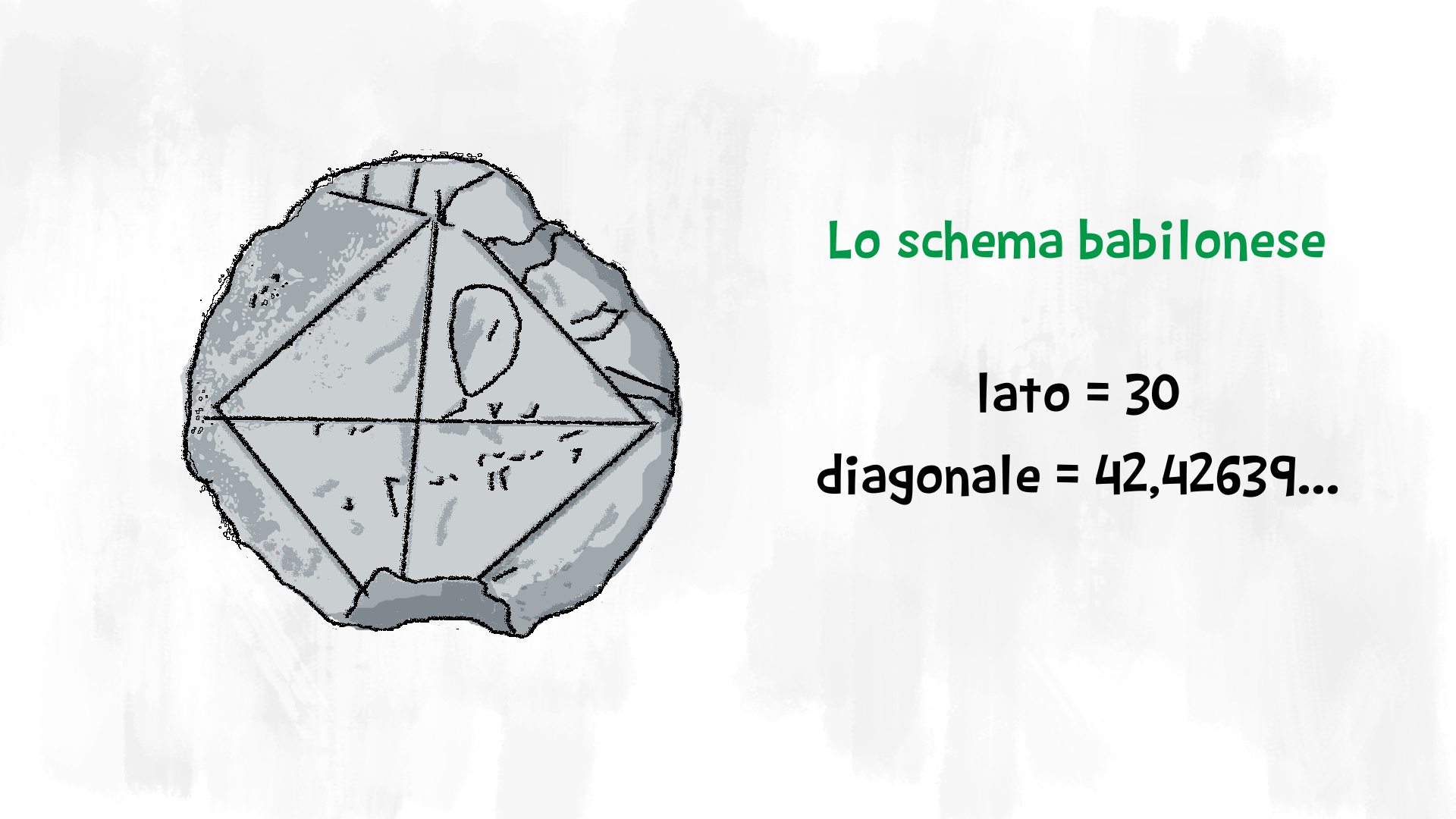
Esistono dimostrazioni del teorema di Pitagora anche precedenti a Pitagora. I Babilonesi osservarono le pavimentazioni tipiche orientali. Scomponendo il quadrato più grande in triangolini, riuscirono ad ottenerne esattamente tanti quanti la somma dei triangolini che compongono i due quadrati più piccoli. Una tavoletta con disegnato un quadrato, dimostra che i Babilonesi conoscevano già il teorema di Pitagora: vi è infatti disegnato un quadrato con le due diagonali. Sul lato del quadrato è segnato il numero £$ 30 $£, su una diagonale i numeri £$ 1,414213… $£ e £$ 42,42639… $£, tutti scritti con il loro sistema sessagesimale: il primo è un’approssimazione del numero £$ \sqrt 2 $£, il secondo è il prodotto di £$ 30 $£ per il primo dei due numeri. I Babilonesi avevano già scoperto una delle proprietà che seguono dal teorema di Pitagora, come vedremo nelle prossime lezioni.
Gli Egizi utilizzavano il teorema di Pitagora per le loro opere architettoniche: aiutandosi con una corda, trovarono il modo di realizzare degli angoli retti attraverso le terne pitagoriche. Questa tecnica si rivelò utilissima per costruire le piramidi, che possiamo ancora ammirare dopo migliaia di anni.
Anche i Cinesi conoscevano il teorema di Pitagora già nel 1000 a.C. e riuscirono a dimostrarlo a partire da una canna di bambù piegata dal vento. Sapendo che la canna si è spezzata ad una certa altezza e conoscendo la distanza a cui la punta della canna tocca il terreno, si può trovare la lunghezza della parte spezzata, cioè la lunghezza dell’ipotenusa del triangolo rettangolo che si è formato.
