Le terne pitagoriche e l'inverso del teorema di Pitagora
Le terne pitagoriche e l’inverso del teorema di Pitagora sono concetti matematici intrinsecamente legati alla geometria euclidea e alla teoria dei numeri, offrendo intuizioni profonde nelle relazioni tra i lati di un triangolo rettangolo. Questi concetti non solo hanno profonde implicazioni teoriche ma trovano anche applicazioni pratiche in vari campi.
Una terna pitagorica consiste in un insieme di tre numeri interi positivi che soddisfano la relazione espressa dal teorema di Pitagora, secondo cui in un triangolo rettangolo la somma dei quadrati dei cateti è uguale al quadrato dell’ipotenusa. Le terne pitagoriche sono quindi triplette di numeri, come (3, 4, 5) o (5, 12, 13), che rispettano questa specifica relazione numerica.
L’inverso del teorema di Pitagora estende questa relazione ai casi in cui non si ha un triangolo rettangolo. Se la somma dei quadrati dei lati più corti è maggiore del quadrato del lato più lungo, allora il triangolo è acutangolo, con tutti e tre gli angoli acuti. Se invece la somma è minore, il triangolo è ottusangolo, con un angolo ottuso. Questa estensione permette di utilizzare i principi del teorema di Pitagora ben oltre i limiti dei triangoli rettangoli, ampliando la sua applicabilità a una gamma più ampia di problemi geometrici e di misurazione.
Vediamoli meglio.
Come costruire angoli retti con il teorema di Pitagora
Piramidi e angoli retti
Le moderne ditte di costruzioni utilizzano i mezzi più tecnologici per realizzare linee dritte e angoli retti, in modo che gli edifici siano stabili e anche semplici da costruire.
Ma nell’antichità non era così banale costruire basamenti quadrati per le costruzioni. Come facevano per esempio gli egizi a realizzare le piramidi senza nessuno strumento particolare? Bastava una corda con dei nodi posizionati alla giusta distanza l’uno dall’altro.
Un triangolo con i lati in rapporto £$ 3:4:5 $£ ha per forza un angolo retto. Prova a disegnarlo! Gli Egizi sfruttarono questa proprietà per costruire le piramidi.
Le terne pitagoriche
Per il teorema di Pitagora vale anche l’inverso. L’inverso del teorema di Pitagora dice:
Se riusciamo a costruire un triangolo con i lati di misura £$ a , b $£ e £$ c $£ (numeri naturali) tali per cui vale la relazione £$ a^2 + b^2 = c^2 $£, allora il triangolo è rettangolo.
Tutte le terne di numeri fatte in questo modo sono le terne pitagoriche. Le terne pitagoriche sono numeri naturali per cui riusciamo a scrivere la relazione che abbiamo appena visto. Il £$ 3 $£, il £$ 4 $£ e il £$ 5 $£ formano una terna pitagorica: infatti £$ 3^2 + 4^2 = 9 + 16 = 25 = 5^2 $£. Di conseguenza formano una terna pitagorica anche gli stessi multipli di questi tre numeri! Per esempio, proviamo a moltiplicarli tutti per £$ 2 $£: £$ (3 \cdot 2)^2 + (4 \cdot 2)^2 = 36 + 64 = 100 = (5 \cdot 2)^2 $£
Per questo motivo gli Egiziani riuscivano a costruire angoli retti semplicemente utilizzando una corda con dei nodi: facendo i nodi tutti alla stessa distanza, riuscivano a costruire un triangolo i cui lati formavano una terna pitagorica. Ed ecco applicato l’inverso del teorema di Pitagora: erano riusciti a trovare un triangolo rettangolo!
Conosci altre terne pitagoriche? Prova a trovarle! Conoscerne il più possibile, ti aiuterà a velocizzare gli esercizi. 😉
Trovi la tabella con tutte le formule qui.
Come utilizzare il teorema di Pitagora
Esercizio svolto: triangolo isoscele
Esercizio svolto: rombo
Il teorema di Pitagora ci permette di trovare la misura di tutti i lati di un triangolo rettangolo. Il quadrato costruito sull’ipotenusa £$ (i) $£ è uguale alla somma dei quadrati costruiti sui due cateti £$ (c_1 $£ e £$ c_2) $£.
$$ i^2 = c_1^2 + c_2^2 $$
Possiamo ricavare la stessa relazione anche per i due cateti:
$$ c_1^2 = i^2 – c_2^2 $$
$$ c_2^2 = i^2 – c_1^2 $$
Basta fare attenzione al lato che dobbiamo calcolare: l’ipotenusa è uguale alla somma dei quadrati dei due cateti, mentre ciascuno dei due cateti è uguale alla differenza tra il quadrato dell’ipotenusa e il quadrato dell’altro cateto.

£$ \overline{AB} = \sqrt{\overline{BC}^2 – \overline{AC}^2} \\ \overline{AC} = \sqrt{\overline{BC}^2 – \overline{AB}^2} \\ \overline{BC} = \sqrt{\overline{AB}^2 + \overline{AC}^2} $£
Basta ricordarsi la formula dell’enunciato per ricavare tutte le altre. Estraendo la radice quadrata, troviamo la misura di ciascun lato del triangolo. Ora sei pronto per affrontare gli esercizi sul teorema di Pitagora!
Teorema di Pitagora e poligoni regolari
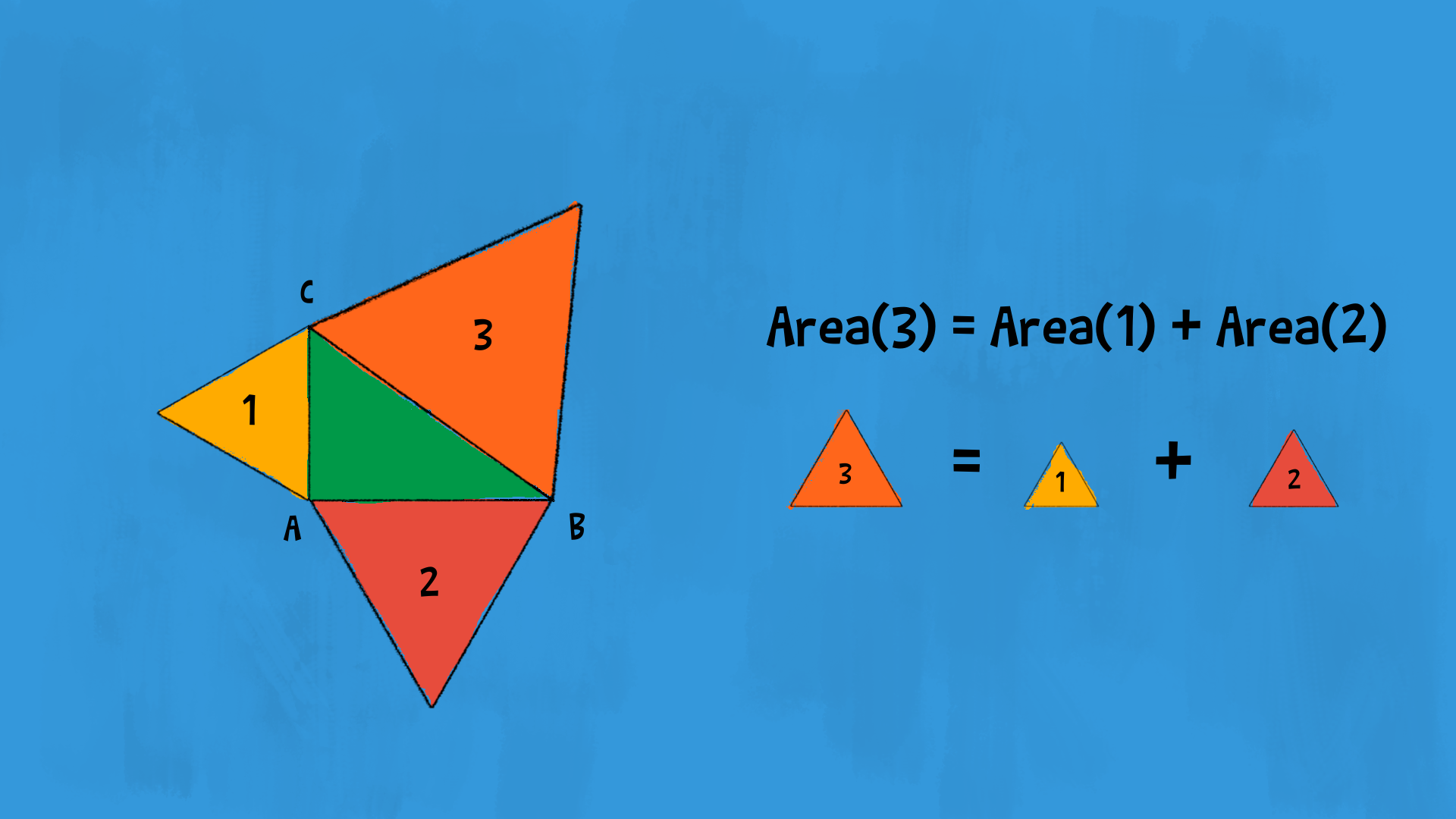
Il teorema di Pitagora funziona anche con altre figure! Se al posto di costruire i quadrati sui cateti e sull’ipotenusa, costruiamo altri poligoni regolari, otteniamo lo stesso risultato.
Prendiamo il nostro triangolo rettangolo con lati di £$ 3 \text{ cm} $£, £$ 4 \text{ cm} $£ e £$ 5 \text{ cm} $£.
Proviamo a disegnare un triangolo equilatero sull’ipotenusa e due triangoli equilateri sui due cateti del triangolo rettangolo. Facendo qualche calcolo, puoi dimostrare che la somma delle aree dei due triangoli equilateri costruiti sui cateti è uguale all’area del triangolo costruito sull’ipotenusa. Mettiti alla prova!
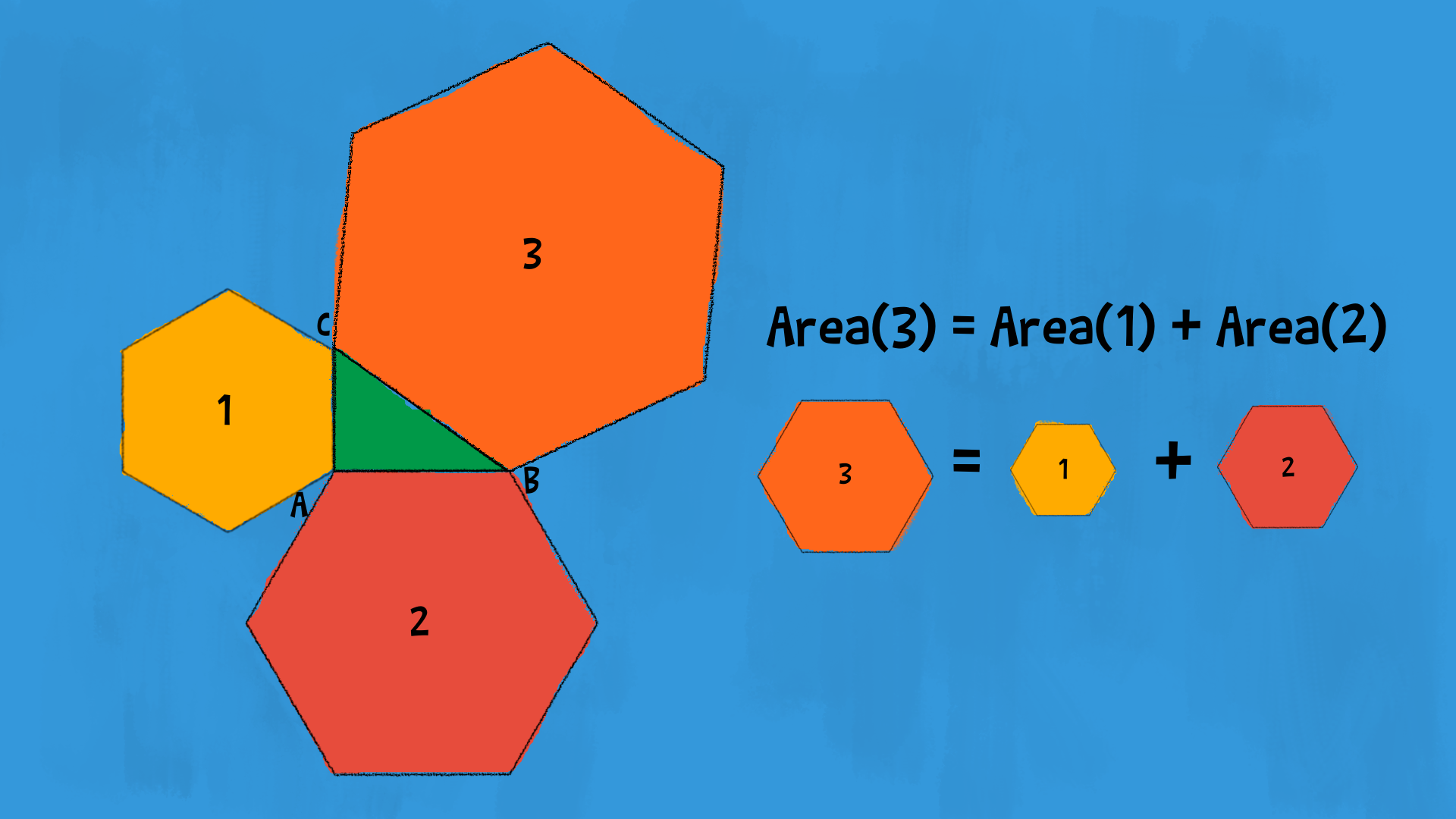
Proviamo poi con un esagono: l’area dell’esagono regolare con lato uguale all’ipotenusa del triangolo rettangolo è uguale alla somma delle aree degli esagoni regolari con lato uguale al cateto minore e al cateto maggiore del triangolo rettangolo. Ti ricordi come si calcola l’area di un esagono? Dobbiamo moltiplicare il perimetro per l’apotema. Ma come facciamo a trovare l’apotema? Possiamo utilizzare di nuovo il teorema di Pitagora: possiamo dividere l’esagono in sei triangolini equilateri. Scegliamone uno: l’apotema è l’altezza di questo triangolo equilatero, e lo divide in due triangoli rettangoli su cui possiamo applicare il teorema di Pitagora. Una volta trovata l’altezza, fai qualche conto e verifica che il teorema di Pitagora vale anche in questo caso: l’area dell’esagono costruito sull’ipotenusa è uguale alla somma delle aree dei due esagoni costruiti sui cateti del triangolo rettangolo di partenza.
Sorpreso? Controlla tu stesso e scoprirai che vale anche con tutti gli altri poligoni regolari!
