Il primo e il secondo teorema di Euclide: formule e definizione
I teoremi di Euclide, generalmente associati al matematico greco Euclide, sono un insieme di proposizioni e conclusioni fondamentali nella geometria euclidea. Euclide ha raccolto e sistematizzato queste conoscenze nel suo famoso trattato, gli “Elementi“, che per secoli è stato il testo di riferimento per l’insegnamento della matematica.
A che cosa servono i criteri di similitudine dei triangoli? Ci permettono di dimostrare i teoremi di Euclide. Vediamo le proprietà dei triangoli simili e alcune dimostrazioni!
Questi teoremi sono fondamentali non solo in geometria, ma anche in molte altre aree della matematica e delle sue applicazioni. Vengono utilizzati per risolvere problemi che riguardano le misure, le proporzioni e le relazioni spaziali in geometria piana e spaziale. La loro importanza risiede nella capacità di fornire una base logica e sistematica per la comprensione delle proprietà geometriche e delle loro relazioni reciproche.
Vediamoli insieme!
Vuoi testare la tua preparazione? Prova il nostro quiz!
- I triangoli rettangoli e i teoremi di Euclide
- Primo teorema di Euclide: enunciato e dimostrazione
- Secondo teorema di Euclide: enunciato e dimostrazione
- Le formule inverse del secondo teorema di Euclide
- La tabella riassuntiva del primo e secondo teorema di Euclide
- Ripassa per l'interrogazione sui teoremi di Euclide
- Sfida sui teoremi di Euclide
I triangoli rettangoli e i teoremi di Euclide
£$ CH $£ altezza relativa all’ipotenusa
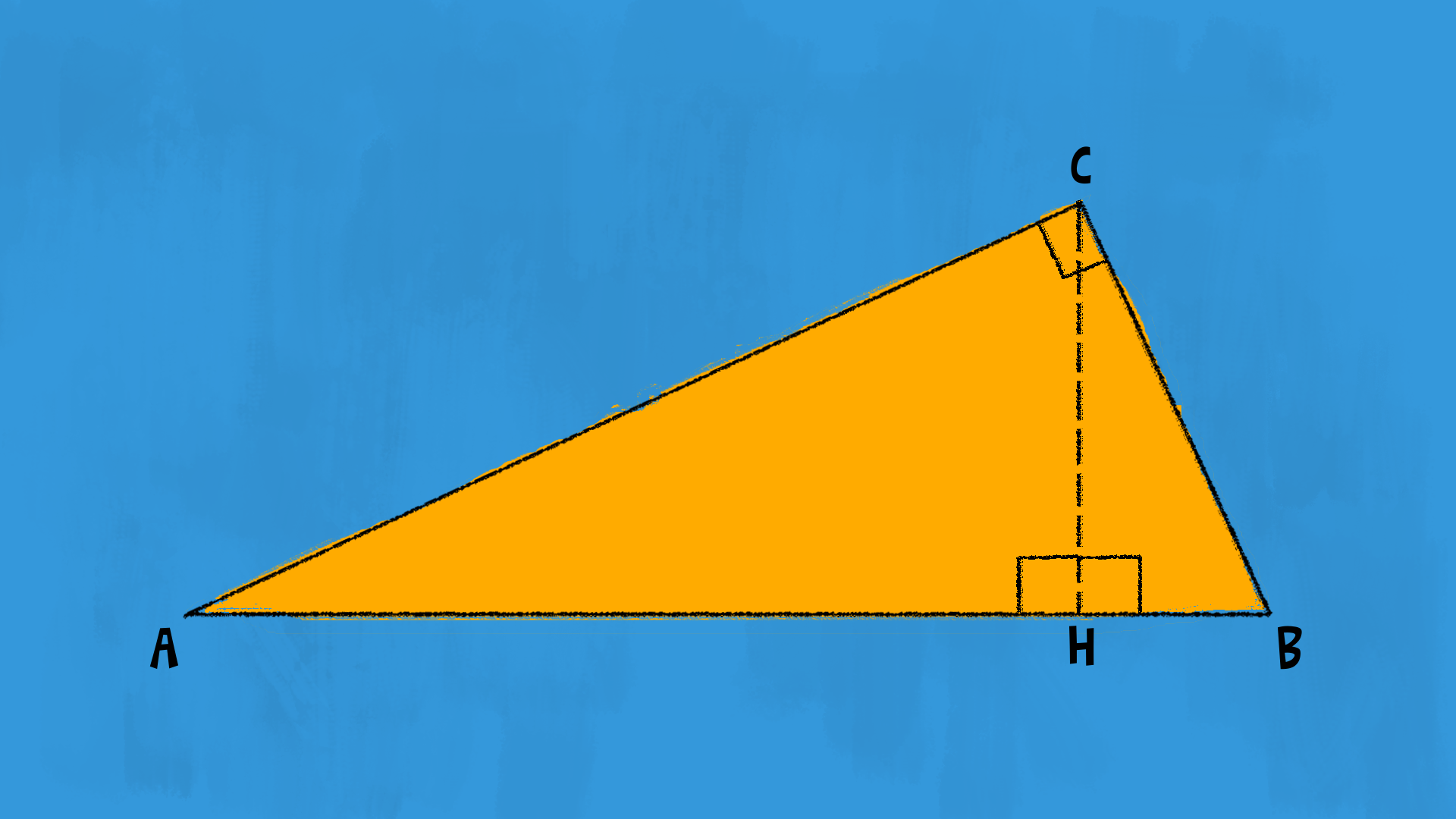
Caratteristiche dei tre triangoli

I teoremi di Euclide, così come il teorema di Pitagora, parlano di triangoli rettangoli.
Tracciamo l’altezza relativa all’ipotenusa di un triangolo rettangolo £$ \stackrel{\triangle}{ABC} $£ retto in £$ C $£. L’ipotenusa è il lato £$ AB $£ e l’altezza relativa all’ipotenusa è £$ CH $£. Il punto £$ H $£ divide l’ipotenusa in due parti:
- £$ AH $£ è la proiezione del cateto £$ AC $£ sull’ipotenusa;
- £$ HB $£ è la proiezione del cateto £$ CB $£ sull’ipotenusa.
Quanti triangoli rettangoli riesci a vedere nella figura così tracciata? Ben 3! Il primo triangolo è £$ \stackrel{\triangle}{ABC} $£. L’altezza £$ CH $£ divide questo triangolo in altri due triangoli rettangoli. Gli angoli retti hanno vertice in £$ H $£. Il triangolo £$ \stackrel{\triangle}{ACH} $£ ha come ipotenusa £$ AC $£ e come cateti £$ CH $£ e £$ AH $£. Il triangolo £$ \stackrel{\triangle}{BCH} $£ ha come ipotenusa £$ BC $£ e come cateti £$ CH $£ e £$ BH $£.
I triangoli rettangoli £$ \stackrel{\triangle}{ABC} $£, £$ \stackrel{\triangle}{ACH} $£ e £$ \stackrel{\triangle}{BCH} $£ hanno sempre due angoli congruenti, quello retto e un altro angolo, quindi sono simili!
Proprietà dei triangoli simili
Se due triangoli sono simili, valgono le seguenti proprietà:
- il rapporto tra i perimetri è uguale al rapporto tra due lati omologhi;
- il rapporto tra le aree è uguale al quadrato del rapporto tra due lati omologhi;
- il rapporto tra le basi è uguale al rapporto tra le altezze.
Dimostriamo solo l’ultima proprietà applicando il primo criterio di similitudine.
Primo teorema di Euclide: enunciato e dimostrazione
Enunciato
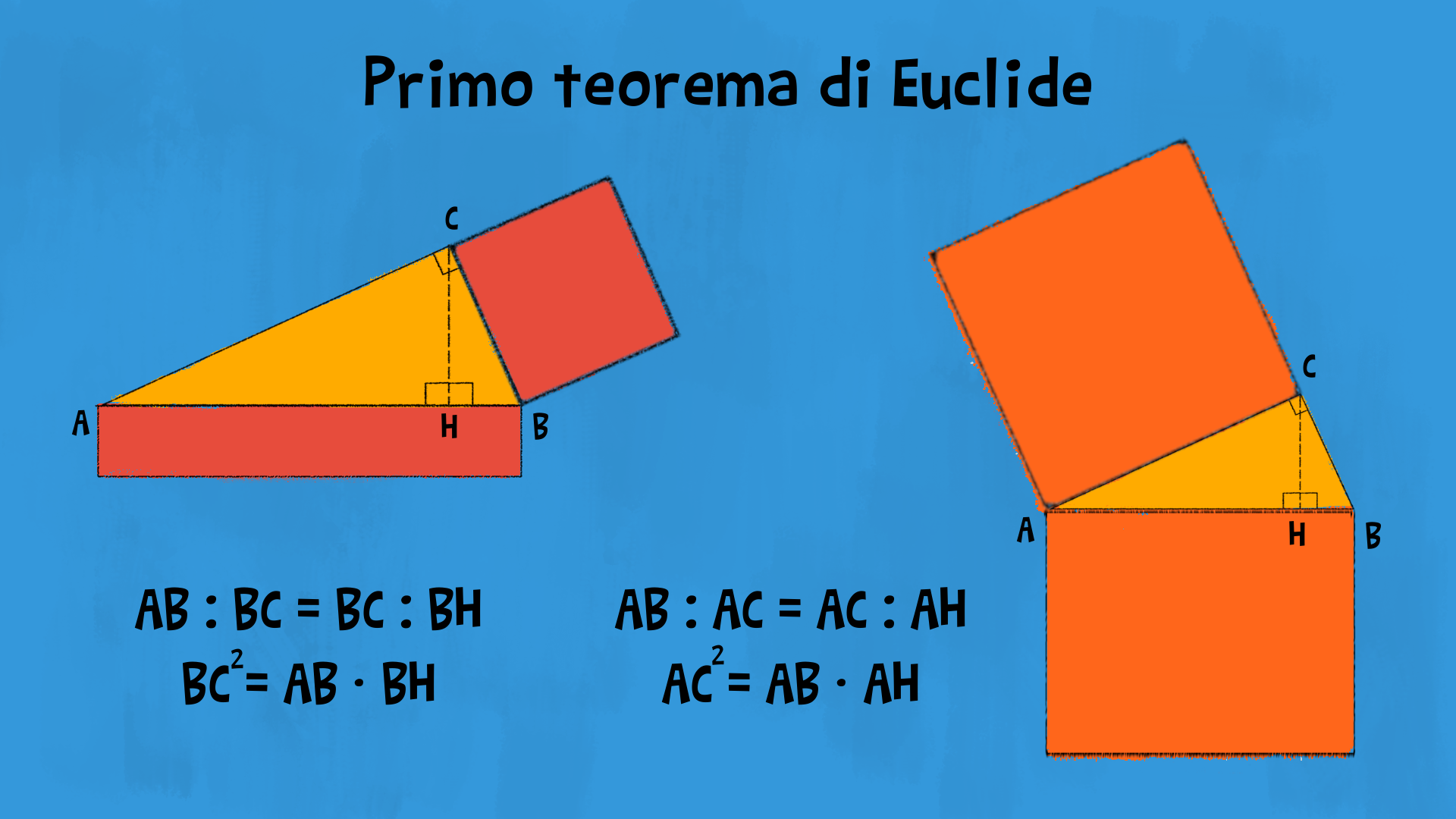
Dimostrazione
Abbiamo visto che, tracciando l’altezza relativa all’ipotenusa di un triangolo rettangolo £$ \stackrel{\triangle}{ABC} $£ retto in £$ C $£, otteniamo due nuovi triangoli rettangoli simili a quello di partenza, £$ \stackrel{\triangle}{ACH} $£ e £$ \stackrel{\triangle}{BCH} $£.
Se confrontiamo i due triangoli £$ \stackrel{\triangle}{ABC} $£ e £$ \stackrel{\triangle}{ACH} $£, il rapporto tra le ipotenuse è uguale al rapporto tra i cateti minori. Se confrontiamo i due triangoli £$ \stackrel{\triangle}{ABC} $£ e £$ \stackrel{\triangle}{BCH} $£, il rapporto tra le ipotenuse è uguale al rapporto tra i cateti maggiori. Triangoli simili hanno lati corrispondenti in proporzione. Allora possiamo rappresentare queste relazioni utilizzando proprio le proporzioni:
- £$ AB : AC = AC : AH $£;
- £$ AB : BC = BC : BH $£.
Ricordi come si chiama l’elemento che in una proporzione occupa entrambe le posizioni dei medi? È il medio proporzionale!
Possiamo enunciare allora il primo teorema di Euclide:
In un triangolo rettangolo un cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto su di essa.
Ma ecco un’interpretazione geometrica interessante di questo teorema… Ricordi la proprietà fondamentale delle proporzioni? Il prodotto dei medi è uguale al prodotto degli estremi. Quindi possiamo riscrivere le due proporzioni nel modo seguente:
- £$ AC^2=AB\cdot AH $£;
- £$ BC^2=AB\cdot BH $£.
£$ AC^2 $£ è l’area del quadrato costruito sul lato £$ AC $£ e £$ AB\cdot AH $£ è l’area di un rettangolo di lati £$ AB $£ e £$ AH$£. £$ BC^2 $£ è l’area del quadrato costruito sul lato £$ BC $£ e £$ AB\cdot BH $£ è l’area di un rettangolo di lati £$ AB $£ e £$ BH$£.
Possiamo riscrivere il primo teorema di Euclide così:
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha come lati l’ipotenusa e la proiezione del cateto su di essa.
Primo teorema con le similitudini
Primo teorema di Euclide: In un triangolo rettangolo, un cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto stesso sull’ipotenusa.
Si può dimostrare tramite il primo criterio di similitudine dei triangoli.
Secondo teorema di Euclide: enunciato e dimostrazione
Enunciato
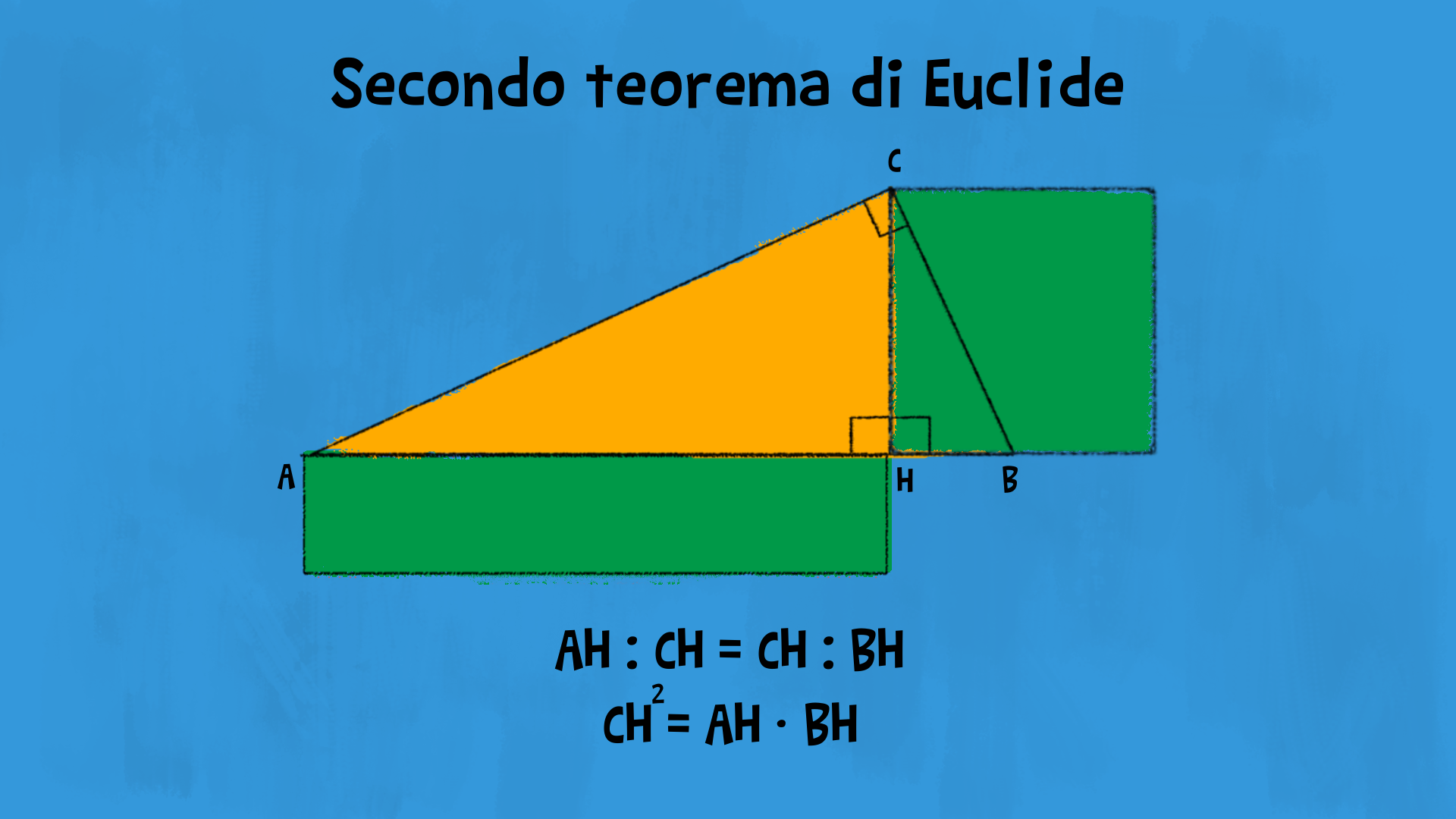
Dimostrazione
Confrontiamo ora i due triangoli £$ \stackrel{\triangle}{ACH} $£ e £$ \stackrel{\triangle}{BCH} $£. Anch’essi sono simili! Quindi, il rapporto tra i cateti minori è uguale al rapporto tra i cateti maggiori. Possiamo rappresentare questa relazione utilizzando le proporzioni: £$ AH : CH = CH : BH $£. Questa volta è l’altezza £$ CH $£ ad essere medio proporzionale.
Possiamo enunciare allora il secondo teorema di Euclide:
In un triangolo rettangolo l’altezza relativa all’ipotenusa è medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa.
Anche in questo caso possiamo trovare un’interessante interpretazione geometrica riscrivendo la proporzione in questo modo: £$ CH^2=AH\cdot BH $£.
£$ CH^2 $£ è l’area del quadrato costruito sull’altezza £$ CH $£ e £$ AH\cdot BH $£ è l’area di un rettangolo di lati £$ AH $£ e £$ BH$£.
Possiamo riscrivere il secondo teorema di Euclide così:
In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha come lati le proiezioni del cateti sull’ipotenusa.
Le formule inverse del secondo teorema di Euclide
Le formule inverse del secondo teorema di Euclide sono:
$$\overline{AH}=\dfrac{\overline{CH}^2}{\overline{BH}}$$ $$\overline{BH}=\dfrac{\overline{CH}^2}{\overline{AH}}$$
Secondo teorema con le similitudini
Secondo Teorema di Euclide: In un triangolo rettangolo, l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei cateti sull’ipotenusa.
Per la dimostrazione applichiamo il primo criterio di similitudine e la proprietà transitiva.
La tabella riassuntiva del primo e secondo teorema di Euclide
Hai bisogno di ripassare? Allenati con la nostra tabella e fai esercizio!

Ripassa per l’interrogazione sui teoremi di Euclide
Imparare ad applicare i teoremi di Euclide con le similitudini è importantissimo: ti saranno molto utili negli esercizi!
Prova a rispondere alle domande dell’interrogazione e poi corri ad allenarti con gli esercizi!
Sfida sui teoremi di Euclide
Sfida:
Soluzione:
Un cono di gelato base costa 2,5 euro. Ti conviene far pagare 5 euro il cono più grande, che ha tutte le dimensioni raddoppiate? Pensa ai coni come a dei triangoli isosceli e usa i teoremi di Euclide per le similitudini!
