La sfera: definizione, superficie e volume

Nel mondo della geometria, le forme tridimensionali rivestono un ruolo di primaria importanza e tra queste, la sfera è senza dubbio una delle più affascinanti e rilevanti. In questo articolo esploreremo le caratteristiche fondamentali delle sfere, approfondendo in modo pratico e diretto il loro studio.

Una sfera, infatti, non è solo un’immagine comune che associamo a oggetti come palloni o pianeti, ma rappresenta un concetto geometrico chiave, un modello matematico che ha un’enorme quantità di applicazioni pratiche nel mondo reale. Ciò che distingue una sfera è la sua simmetria perfetta: ogni punto sulla superficie di una sfera dista esattamente lo stesso dal suo centro e questa proprietà la rende unica tra tutte le forme tridimensionali.

Inoltre, uno degli aspetti più intriganti delle sfere riguarda il calcolo della loro superficie e del loro volume. Entrambi questi calcoli richiedono l’uso di una costante matematica fondamentale, il pi greco. Ma come si arriva a determinare la superficie e il volume di una sfera? E quali sono le formule precise che possiamo utilizzare?

Quindi, se vi siete mai chiesti che cosa esattamente sia una sfera, come si possa calcolare la sua superficie e il suo volume, o semplicemente desiderate rinfrescare le vostre conoscenze geometriche, questo articolo fa al caso vostro. Siete pronti a iniziare? Avanti, c’è tanto da scoprire!

• Che cos'è la sfera
• Quali sono le sezioni della sfera
• Come si calcola la superficie della sfera
• Come si calcola il volume della sfera

Che cos’è la sfera

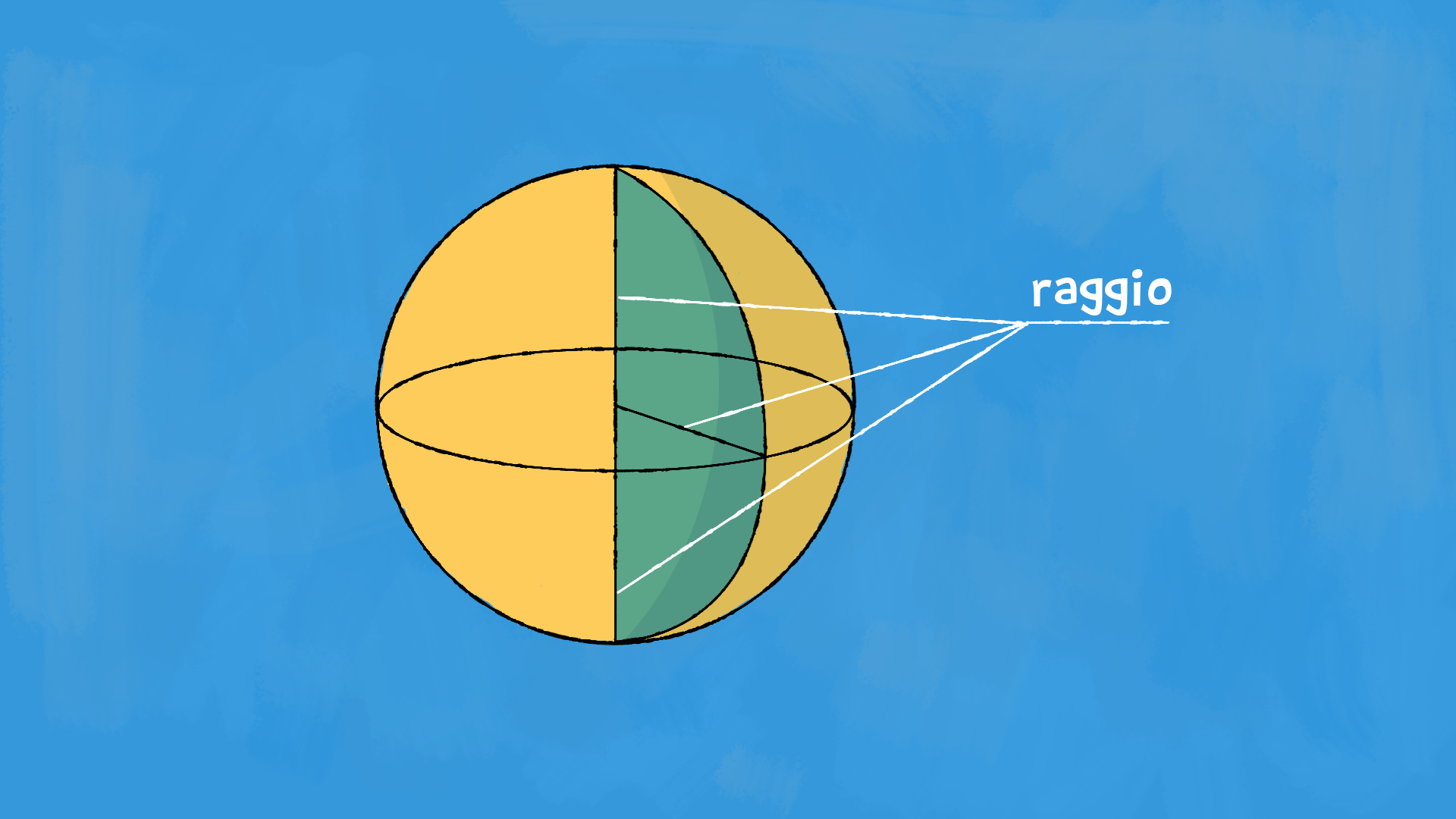
Per ottenere una sfera, facciamo ruotare un semicerchio di un giro completo attorno al suo diametro che rimane fisso nella rotazione.

Una sfera ha un centro, il centro del semicerchio, e un raggio, che coincide con quello del semicerchio.

Pensiamo a una sfera come ad un’arancia. La buccia è la superficie sferica: è fatta da tutti i punti dello spazio che hanno distanza dal centro uguale al raggio.

Il diametro di una circonferenza è la sua corda massima, cioè la corda passante per il centro che congiunge due punti della circonferenza. Anche la sfera ha un diametro: è il segmento passante per il centro della sfera che collega due punti della superficie sferica.

Quali sono le sezioni della sfera

Con qualsiasi piano noi decidiamo di affettare una sfera, otteniamo sempre sezioni circolari. Più ci allontaniamo dal centro, più le sezioni diventano piccole.

La sezione più grande si chiama cerchio massimo e si ottiene quando affettiamo la sfera con un piano che passa per il centro.
In ogni sfera ci sono infiniti cerchi massimi e sono tutti congruenti tra loro: hanno raggio uguale a quello della sfera!

La circonferenza di un cerchio massimo è una circonferenza massima. Le circonferenze massime sono le circonferenze più lunghe che si possono disegnare su una sfera. Sul mappamondo l’equatore e i meridiani sono tutte circonferenze massime. I paralleli invece (tranne l’equatore) non sono circonferenze massime: sono più piccole!

Come si calcola la superficie della sfera

Calcolare la superficie di una sfera non è un affare semplice. Hai mai provato ad aprire una sfera? È impossibile trovare il suo sviluppo piano!

Andiamo subito al dunque! L’ area della superficie di una sfera di raggio £$ r $£ è $$ S=4\pi r^2 $$ $$ r=\sqrt{\dfrac{S}{4\pi}} $$

Che cosa vuol dire? Sembra molto strano ma in realtà è proprio così: la superficie della sfera è proprio equivalente alla superficie di £$ 4 $£ cerchi massimi, cioè di £$ 4 $£ cerchi di raggio uguale a quello della sfera.

Come si calcola il volume della sfera

E il volume di una sfera? Anche in questo caso non è affatto semplice immaginarlo.

$$V=\dfrac43\pi r^3$$ $$ r=\sqrt[3]{\dfrac{3V}{4\pi}} $$