Formulario di fisica: il campo elettrico

Il campo elettrico è uno dei concetti cardine della fisica che, pur sembrando astratto, gioca un ruolo fondamentale nella nostra vita quotidiana. In termini semplici, il campo elettrico rappresenta l’area attorno a una carica elettrica in cui si manifesta una forza elettrica: se si posiziona una seconda carica all’interno di questo campo, essa subirà una forza dovuta alla presenza del campo stesso.

Immaginate un sasso gettato in uno stagno: le onde che si generano si propagano sull’acqua, influenzando tutto ciò che incontrano sul loro cammino. Analogamente, una carica elettrica crea intorno a sé un “campo" che può influenzare altre cariche presenti nelle sue vicinanze. Quando si parla di campo elettrico, ci si riferisce proprio a questo “spazio d’azione" generato da una carica elettrica.

Nella vita di tutti i giorni, il campo elettrico è presente ovunque, anche se non possiamo vederlo o toccarlo direttamente. In questo articolo, cercheremo insieme di imparare le formule principali che hanno come protagonista il campo elettrico!

• Definizione del campo elettrico
• Relazione tra E ed F
• Campo elettrico di una carica puntiforme
• Il campo elettrico di un piano uniformemente carico
• Campo elettrico generato da un filo infinito uniformemente carico
• Campo elettrico generato da una sfera di raggio £$\vec R$£ uniformemente carica
• Campo elettrico in prossimità della superficie di un conduttore
• Campo elettrico di un cilindro uniformemente carico
• Teorema di Gauss

Definizione del campo elettrico

Il campo elettrico £$\vec E$£ è un campo vettoriale che si manifesta come una modifica dello spazio ed è prodotto dalla presenza di cariche.

Relazione tra E ed F

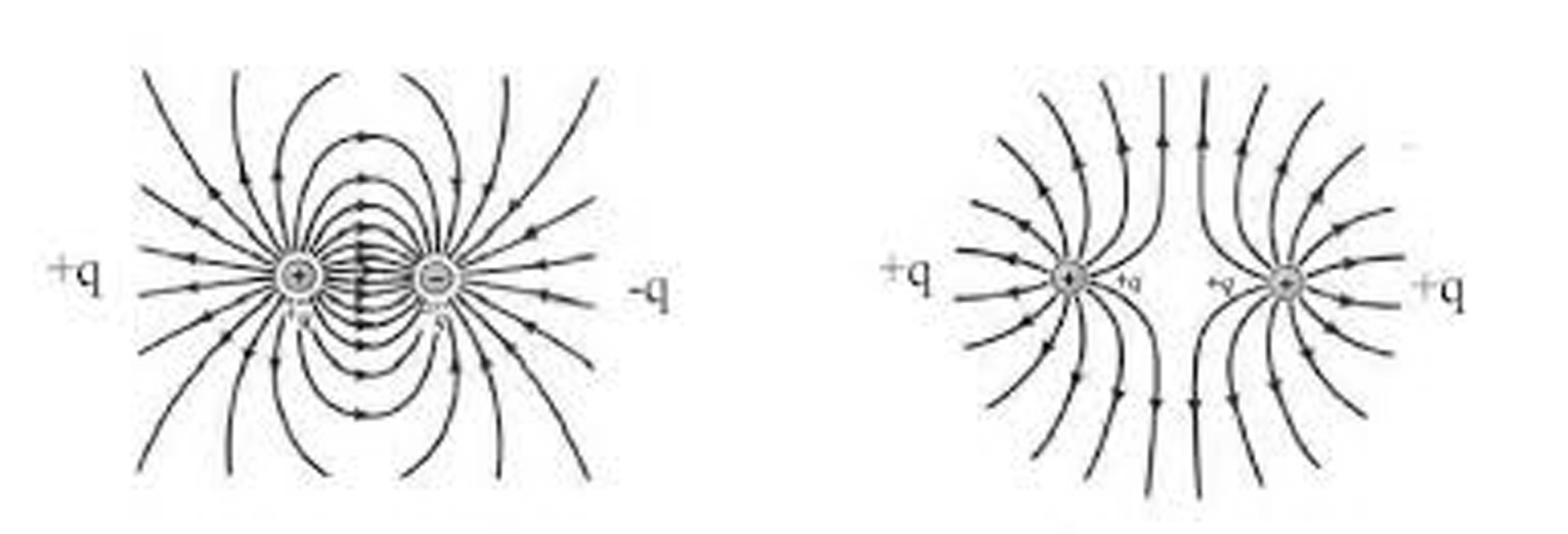
Il campo elettrostatico £$\vec E$£ in un punto dello spazio è il rapporto tra la forza elettrostatica £$\vec F$£che agisce su una carica di prova £$q$£ e la carica stessa:

$$\vec E = \frac{\vec F}{q}$$

L’unità di misura di £$\vec E$£ nel S.I. è £$\dfrac{N}{C}$£.

Il campo elettrico è rappresentato dalle linee di campo. Nel caso di una carica puntiforme le linee di campo sono uscenti dalla carica positiva e nel caso di una carica negativa sono entranti.

Campo elettrico di una carica puntiforme

La presenza di una carica puntiforme £$ Q $£ in un punto dello spazio genera nello spazio circostante un campo elettrico la cui intensità a distanza £$r$£ dalla carica è:

$$E=k \frac{Q}{r^2}$$

Il campo elettrico di un piano uniformemente carico

Le cariche elettriche sono distribuite uniformemente sulla superficie del piano; il campo elettrico che si genera nello spazio circostante è un campo elettrico uniforme, le cui linee sono rettilinee, equidistanti e parallele. L’intensità di questo campo è:

$$E= \frac{\sigma}{2\epsilon_0}$$

dove £$\sigma$£ è la densità superficiale di carica, cioè £$\sigma=\dfrac{Q}{S}$£ £$ \big( $£nel S.I. si misura in £$\dfrac{C}{m^2} \big)$£.

Campo elettrico generato da un filo infinito uniformemente carico

Le cariche elettriche sono distribuite uniformemente lungo il filo di lunghezza infinita; il campo elettrico che si genera nello spazio circostante è un campo elettrico radiale. L’intensità di questo campo a una distanza £$r$£ dal filo è:

$$E= \frac{\lambda}{2\pi\epsilon_0r}$$

dove £$\lambda$£ è la densità lineare di carica, cioè £$\lambda=\dfrac{Q}{l}$£ £$\big( $£nel S.I. si misura in £$\dfrac{C}{m} \big) $£.

Campo elettrico generato da una sfera di raggio £$\vec R$£ uniformemente carica

Le cariche elettriche sono distribuite uniformemente in tutto il volume della sfera; la carica totale è £$Q$£. Si genera un campo elettrico all’interno e all’esterno della sfera il cui modulo è:

• per [iol_placeholder type="formula" engine="katex" display="inline"]r
• per £$r=R$£: $$E(R)= \frac{Q}{4\pi\epsilon_0R^2}$$ Sulla superficie della sfera il campo elettrico ha valore massimo;
• per £$r>R$£: $$E(r)= \frac{Q}{4\pi\epsilon_0 r^2}$$ All’esterno il campo elettrico decresce con il quadrato della distanza £$r$£ dal centro della sfera; in questo modo è uguale a quello che si otterrebbe se la carica fosse tutta concentrata nel centro.

Campo elettrico in prossimità della superficie di un conduttore

Applicando il teorema di Gauss ad un conduttore elettrostatico in una regione appena esterna alla sua superficie, indicando con £$\sigma$£ la densità superficiale di carica, si ha:

$$E= \frac{\sigma}{\epsilon_0}$$

Questa è l’espressione del teorema di Coulomb.

Campo elettrico di un cilindro uniformemente carico

Le cariche elettriche sono distribuite uniformemente in tutto il volume del cilindro, la carica totale è £$Q$£. Si genera un campo elettrico all’interno e all’esterno del cilindro il cui modulo è:

• per [iol_placeholder type="formula" engine="katex" display="inline"]r
• per £$r>R$£: $$E(r)= \frac{\rho R^2}{2 \epsilon_0 r}$$

dove compare la densità volumica di carica, definita come £$\rho=\dfrac{Q}{V}$£ £$ \big( $£nel S.I. si misura in £$\dfrac{C}{m^3} \big) $£.

Teorema di Gauss

Il flusso del campo elettrico £$\vec E \quad$£ uscente da una qualsiasi superficie chiusa £$\vec S$£, definito come:

$$\Phi_{\vec s}(\vec E) = \oint_s \vec E \cdot d\vec S = \oint_s E \,\cos{\alpha} \,dS$$

è uguale al rapporto tra la somma delle cariche contenute all’interno della superficie e la costante dielettrica del vuoto:

$$\Phi_{\vec S}(\vec E)= \frac{\sum_i q_i}{\epsilon_0}$$