Formulario di fisica: l'equilibrio dei corpi

L’equilibrio dei corpi rappresenta un concetto fondamentale nella fisica classica, un fenomeno che si manifesta ogni giorno intorno a noi, influenzando svariati aspetti della nostra esistenza. Quando parliamo di “equilibrio", ci riferiamo a uno stato di un sistema in cui non si osservano variazioni nel tempo, un momento di stasi che appare come un contrappunto alla tumultuosa dinamica della natura. Ma cosa significa realmente che un corpo è in equilibrio? E come possiamo descriverlo nel contesto fisico?

Un corpo è detto in equilibrio quando le forze esterne che agiscono su di esso si bilanciano a vicenda, risultando in una risultante delle forze pari a zero. Questo implica che il corpo non subirà alcuna accelerazione e, se inizialmente è fermo, rimarrà fermo; se inizialmente è in movimento a velocità costante in una direzione rettilinea, continuerà a muoversi in quella direzione a quella stessa velocità.

Esistono due tipi principali di equilibrio: l’equilibrio stabile e l’equilibrio instabile. Nel primo, se un corpo viene spostato leggermente dalla sua posizione di equilibrio, le forze esterne tendono a riportarlo nella sua posizione originale. Nel secondo, uno spostamento anche minimo dalla posizione di equilibrio può far sì che il corpo si allontani sempre di più da tale posizione, rendendo l’equilibrio instabile e precario.

Scopriamo insieme le formule principale!

• Condizione di equilibrio di un punto materiale
• Condizione di equilibrio di un corpo rigido
• Definizione di momento di una forza
• Energia cinetica rotazionale e momento d'inerzia
• Energia cinetica totale del corpo rigido

Condizione di equilibrio di un punto materiale

Condizione necessaria e sufficiente perché un punto materiale sia in equilibrio è che la somma vettoriale delle forze che agiscono su di esso sia nulla.

$$\vec R=\sum_{i} \vec F_{i} =0$$

Tale condizione impedisce il moto di traslazione del corpo.

Condizione di equilibrio di un corpo rigido

Condizione necessaria e sufficiente perché un corpo rigido sia in equilibrio è che la somma vettoriale delle forze che agiscono su di esso e dei momenti delle forze siano nulli.

$$\vec R=\sum_{i} \vec F_i =0$$

Tale condizione impedisce il moto di traslazione del corpo.

$$\vec M_{tot} =\sum_{i} \vec M_i =0$$

Tale condizione impedisce il moto di rotazione del corpo.

Definizione di momento di una forza

Il momento $\vec M$ di una forza $\vec F$ applicata in $P$ rispetto al punto $O$ è:

$$\vec M=\vec r \wedge \vec F=\overrightarrow{OP} \wedge \vec F$$

Energia cinetica rotazionale e momento d’inerzia

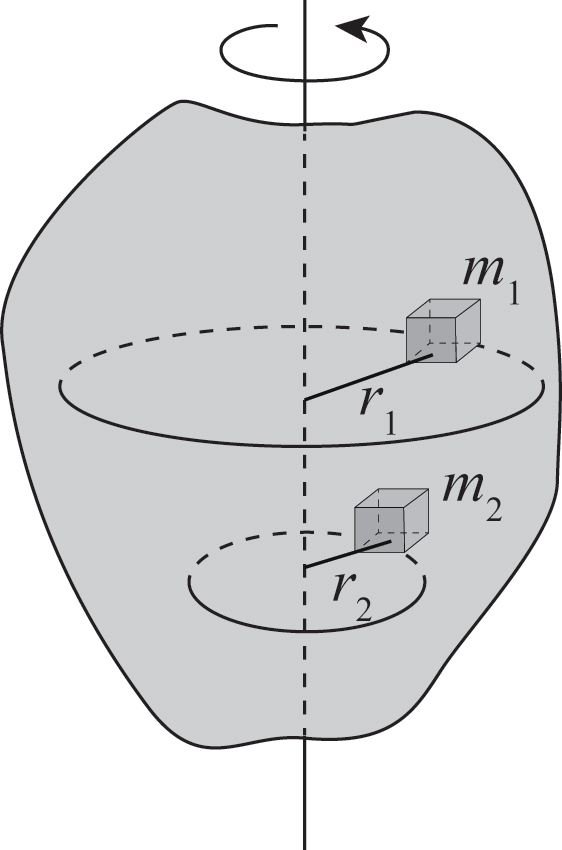
L’energia cinetica di un corpo rigido in rotazione con velocità angolare $\omega$ intorno a un asse fisso è:
$$E_C=\frac{1}{2} I \omega$$
dove $I$ è il momento d’inerzia del sistema rispetto all’asse di rotazione. Nel S.I. l’unità di misura di $I$ è $kg\cdot m^2$. Il momento d’inerzia quantifica la resistenza del corpo al moto rotazionale.
$I$ assume valori diversi a seconda della geometria del corpo rigido e della sua composizione. In generale:
$$I=\sum_{i} m_i\cdot r_i^2$$

Energia cinetica totale del corpo rigido

Un corpo rigido che rotola senza strisciare possiede un’energia cinetica di traslazione dovuta alla sua velocità $v$ e un’energia cinetica rotazionale dovuta al moto di rotazione con velocità $\omega$. Quindi l’energia cinetica totale è:

$$E_C^{tot}=\frac{1}{2} mv^2+ \frac{1}{2} I \omega^2$$