L'iperbole: formulario per risolvere i problemi
Un’iperbole è una curva geometrica formata da due parti simmetriche, chiamate rami, che si allontanano l’uno dall’altro all’infinito.
Le formule dell’iperbole sono necessarie per risolvere i problemi di geometria analitica. Scopri in questa lezione il formulario completo dell’iperbole ed esercitati subito con fuochi, asintoti, eccentricità e sdoppiamento dell’iperbole!
In questa lezione troverai:
- l’equazione canonica dell’iperbole
- le coordinate di vertici e fuochi e le equazioni degli asintoti di un’iperbole con fuochi sull’asse delle ascisse
- le coordinate di vertici e fuochi e le equazioni degli asintoti di un’iperbole con fuochi sull’asse delle ordinate
- le formule dell’eccentricità dell’iperbole
- la formula di sdoppiamento dell’iperbole
- le principali formule dell’iperbole equilatera riferita agli asintoti
- Forma canonica dell'iperbole
- Formule iperbole con fuochi sull'asse x
- Formule iperbole con fuochi sull'asse y
- Formule dell'eccentricità dell'iperbole
- Formula di sdoppiamento dell'iperbole
- Formule dell'iperbole equilatera riferita agli asintoti
Forma canonica dell’iperbole
La forma canonica dell’iperbole è un’espressione che rappresenta l’equazione di un’iperbole in modo standardizzato, cioè in una forma che facilita la comprensione delle proprietà geometriche e matematiche dell’iperbole.
La forma canonica dell’iperbole dipende dal segno del termine noto a destra dell’uguale.
- Se l’iperbole ha i fuochi sull’asse £$x$£ allora l’equazione canonica è $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$
- Se l’iperbole ha i fuochi sull’asse £$y$£ allora l’equazione canonica è $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$$
Formule iperbole con fuochi sull’asse x
L’iperbole £$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$£ ha
- gli asintoti di equazione £$y=\pm\frac{b}{a}x$£
- i fuochi di coordinate £$(\pm c;0)$£ con £$c=\sqrt{a^2+b^2}$£
- i vertici di coordinate £$(\pm a; 0)$£
Formule iperbole con fuochi sull’asse y
L’iperbole £$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$£ ha
- gli asintoti di equazione £$y=\pm\frac{b}{a}x$£
- i fuochi di coordinate £$(0;\pm c)$£ con £$c=\sqrt{a^2+b^2}$£
- i vertici di coordinate £$(0; \pm b)$£
Formule dell’eccentricità dell’iperbole
L’eccentricità dell’iperbole è una misura della sua deviazione dalla circolarità. È definita come il rapporto tra la distanza focale e la lunghezza del semiasse trasverso. L’eccentricità dell’iperbole è:
- £$e=\frac{c}{a}$£ se i fuochi sono sull’asse £$x$£
- £$e=\frac{c}{b}$£ se i fuochi sono sull’asse £$y$£
Formula di sdoppiamento dell’iperbole
Per calcolare l’equazione di una retta tangente all’iperbole in un suo dato punto £$P(x_P;y_P)$£ usiamo la formula di sdoppiamento: $$\frac{x\cdot x_P}{a^2}-\frac{y\cdot y_P}{b^2}=\pm1$$
La formula di sdoppiamento dell’iperbole è una tecnica utilizzata per semplificare le equazioni delle iperbole. Consiste nel riscrivere l’equazione dell’iperbole in modo da evidenziare due termini quadratici che possono essere scritti come il quadrato di una differenza o di una somma. Questo permette di semplificare l’equazione e di identificare più facilmente le caratteristiche dell’iperbole, come i suoi asintoti e la sua eccentricità.
Formule dell’iperbole equilatera riferita agli asintoti
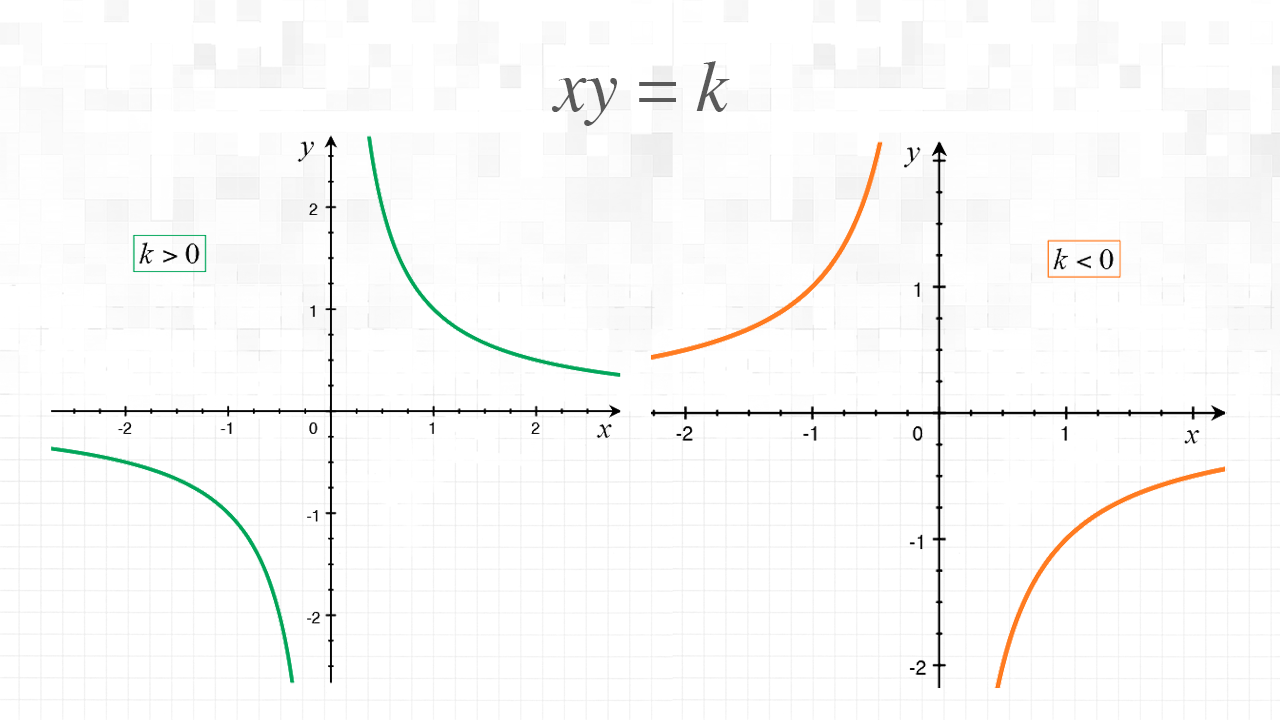
L’iperbole equilatera riferita agli asintoti ha equazione £$xy=\pm k$£ con £$k=\frac{a^2}{2}$£.
Gli elementi principali sono:
- gli asintoti sono gli assi cartesiani £$x=0$£ e £$y=0$£
- i vertici hanno coordinate:
- £$V_1(-\sqrt k;-\sqrt k)$£ e £$V_2(\sqrt k;\sqrt k)$£ se £$k > 0$£
- £$V_1(-\sqrt{- k};-\sqrt{- k})$£ e £$V_2(\sqrt{- k};\sqrt{- k})$£ se [iol_placeholder type="formula" engine="katex" display="inline"]k
- i fuochi hanno coordinate:
- £$F_1(-\sqrt{2 k};-\sqrt{2 k})$£ e £$F_2(\sqrt{ 2k};\sqrt{ 2k})$£ se £$k > 0$£
- £$F_1(-\sqrt{- 2k};-\sqrt{- 2k})$£ e £$F_2(\sqrt{- 2k};\sqrt{- 2k})$£ se [iol_placeholder type="formula" engine="katex" display="inline"]k
