Le equazioni: principi di equivalenza e soluzioni

Le equazioni rappresentano uno degli strumenti più potenti e versatili della matematica, fungendo da ponte tra l’astrazione pura e l’applicazione pratica nei più svariati contesti. Al loro nucleo, le equazioni sono affermazioni che stabiliscono l’uguaglianza tra due espressioni matematiche, legate da un segno di uguale. Queste espressioni possono variare dalla semplicità di un’equazione lineare ad una variabile, alla complessità di equazioni differenziali che modellano fenomeni fisici dinamici. L’arte di risolvere equazioni consiste nel trovare i valori per le variabili che rendono vera l’affermazione, un processo che affonda le sue radici nei principi fondamentali dell’algebra.

I principi di equivalenza giocano un ruolo cruciale in questo processo. Essi stabiliscono che possiamo eseguire le stesse operazioni su entrambi i lati di un’equazione senza alterarne la validità. Queste operazioni includono l’addizione, la sottrazione, la moltiplicazione e la divisione di termini, nonché operazioni più complesse come l’elevazione a potenza o l’estrazione di radice, purché vengano applicate in modo da non violare le regole fondamentali dell’algebra. Questi principi assicurano che, attraverso una serie di manipolazioni algebriche, possiamo trasformare un’equazione in forme equivalenti che ne facilitano la risoluzione.

Quando si affronta un’equazione, i possibili risultati possono essere classificati in diverse categorie a seconda della natura dell’equazione e delle sue soluzioni. Un’equazione può avere una singola soluzione unica, indicando un punto specifico in cui le due espressioni si equivalgono. Altre equazioni, come quelle di secondo grado, possono avere più soluzioni, riflettendo i punti in cui un polinomio interseca l’asse delle ascisse in un grafico cartesiano. Ci sono anche casi in cui un’equazione può non avere soluzioni reali, specialmente quando coinvolge radici quadrate di numeri negativi (senza considerare i numeri complessi) o quando descrive situazioni fisicamente impossibili. Infine, alcune equazioni sono identità, valide per tutti i valori delle variabili coinvolte, illustrando una verità universale piuttosto che una relazione condizionale.

Scopriamole più nel dettaglio.

• Cosa sono le equazioni equivalenti
• Primo principio di equivalenza
• Secondo principio di equivalenza
• Verifica della soluzione di un'equazione
• Soluzioni: determinata, indeterminata, impossibile

Cosa sono le equazioni equivalenti

Due espressioni sono equivalenti se danno lo stesso risultato. Cosa possiamo dire di due equazioni equivalenti?
Due equazioni sono equivalenti se hanno la stessa soluzione.

Che cos’è la soluzione di un’equazione? La soluzione (o radice) dell’equazione è quel valore che, sostituito all’incognita, rende l’equazione un’identità.

Tornando alla nostra bilancia, la soluzione di un’equazione è quel valore che, se messo al posto dell’incognita, lascia la bilancia in equilibrio.

Due equazioni che hanno la stessa soluzione, sono equivalenti: sostituendo lo stesso valore dell’incognita nelle due equazioni, troviamo un’identità. Lo stesso valore è soluzione per entrambe le equazioni.

Primo principio di equivalenza

Come funziona il primo principio?

Regola del trasporto

Regola di cancellazione

Non sempre è facile riconoscere due equazioni equivalenti, soprattutto se non sono scritte in forma normale. Esistono dei principi che ci permettono di ottenere un’equazione equivalente a partire da un’altra.

Il primo principio di equivalenza dice che sommando o sottraendo una stessa quantità ad entrambi i membri di un’equazione, otteniamo un’equazione equivalente.

Esempio: £$ 2x – 3 = 15 $£ è equivalente a £$ 2x – 3 + 8 = 15 + 8 $£, ma anche a £$ 2x – 3 – 1 = 15 – 1 $£.

Una conseguenza del primo principio di equivalenza è la regola del trasporto: “trasportando" un termine da una parte all’altra dell’uguale e cambiandone il segno, otteniamo un’equazione equivalente.

Esempio: applichiamo il primo principio di equivalenza all’equazione £$ 2x – 3 = 15 $£ e sommiamo £$ 3 $£ ad entrambi i membri: £$ 2x – 3 + 3 = 15 + 3 \rightarrow 2x = 15 + 3 $£. È come aver trasportato il £$ 3 $£ dall’altra parte dell’uguale cambiandogli di segno: £$ 2x = 15 + 3 $£

Un’altra conseguenza del primo principio è la regola di cancellazione: se due termini uguali (stesso valore assoluto e stesso segno) si trovano in due membri diversi dell’equazione, possiamo “cancellarli" e trovare un’equazione equivalente.

Esempio: £$ 2x – 3 = 15 – 3 $£ è equivalente a £$ 2x = 15 $£ che otteniamo cancellando il £$ -3 $£ a destra e a sinistra dell’uguale.

Secondo principio di equivalenza

Esiste anche un altro modo per individuare un’equazione equivalente: usando le moltiplicazioni e le divisioni.

Il secondo principio di equivalenza dice che moltiplicando o dividendo entrambi i membri per uno stesso numero diverso da 0, otteniamo un’equazione equivalente.

Esempio:

• £$ 4x + 2 = 8 $£ è equivalente all’equazione £$ 2x + 1 = 4 $£ ottenuta dividendo tutti i termini per £$ 2 $£;
• anche le equazioni £$ 2x – 3 = -9 $£ e £$ 3 – 2x = 9 $£ sono equivalenti. Abbiamo moltiplicato entrambi i membri per £$ -1 $£: il risultato è la stessa equazione, ma con tutti i termini cambiati di segno.

È una conseguenza del secondo principio di equivalenza il fatto che la soluzione di un’equazione come £$ 4x = 12 $£ sia £$ x = \frac{12}{4} $£. Possiamo riassumere questa regola con “se da una parte dell’uguale un numero moltiplica, quando lo porto dall’altra parte dell’uguale, deve dividere".

Verifica della soluzione di un’equazione

Come facciamo a capire se la soluzione che abbiamo trovato è corretta? Dobbiamo fare una verifica!

Un po’ come abbiamo già imparato a fare con la divisione: per controllare che il risultato sia corretto, moltiplichiamo il risultato per il divisore. Se otteniamo il dividendo, abbiamo svolto la divisione correttamente!

Esempio:
£$ 561 : 3 = 187 $£ è una divisione corretta perché £$ 187 \cdot 3 = 561 $£

Anche per le equazioni possiamo fare una verifica per controllare se la soluzione che abbiamo trovato è corretta. Come facciamo? Basta sostituire la soluzione che abbiamo trovato al posto dell’incognita. Se otteniamo un’identità, la soluzione dell’equazione è corretta.

Esempio:
£$ 2x + 1 = 7 $£ ha soluzione £$ x = 3 $£. Controlliamo se è corretta sostituendo il £$ 3 $£ al posto della £$ x $£.

£$ 2 \cdot 3 + 1 = 7 \\ 6 + 1 = 7 \\ 7 = 7 $£
Abbiamo trovato un’identità, quindi £$ x = 3 $£ è proprio soluzione dell’equazione.

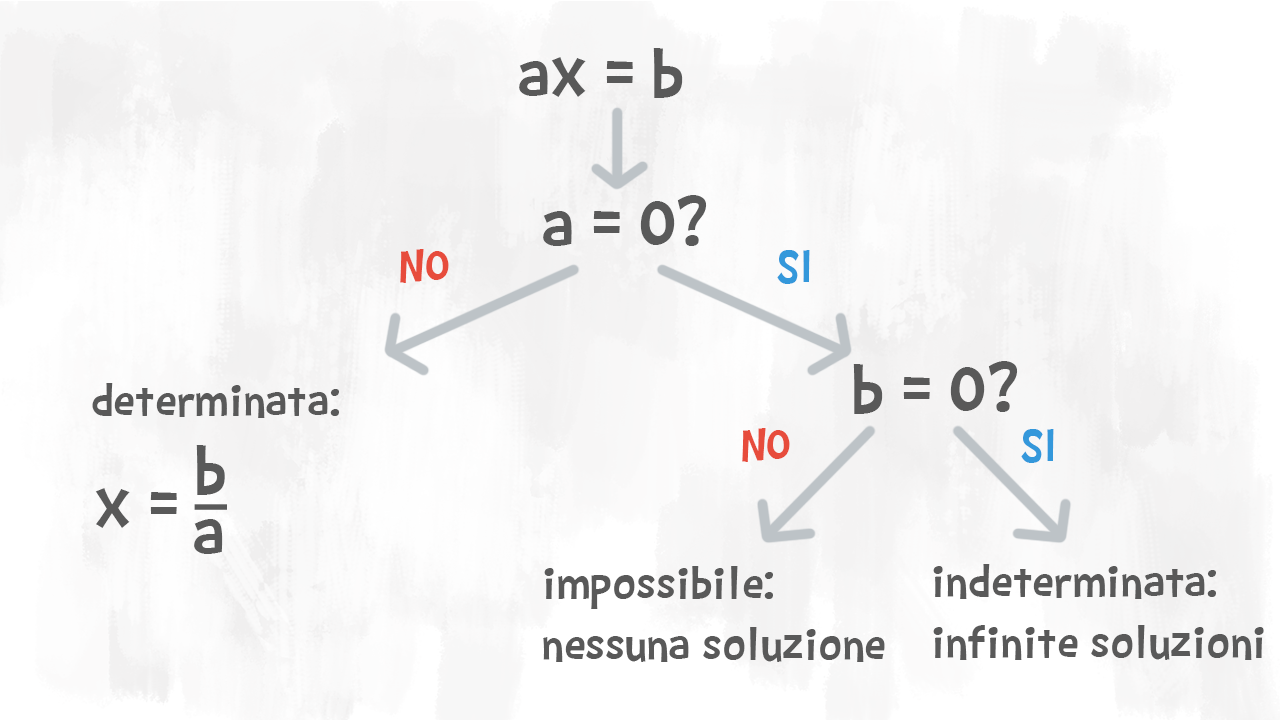
Soluzioni: determinata, indeterminata, impossibile

Equazione determinata

Equazione indeterminata

Equazione impossibile

Tutte le equazioni hanno una soluzione? Non è detto!
Possiamo anche trovarci di fronte ad equazioni che non hanno soluzioni, oppure che hanno infinite soluzioni.

Un’equazione è determinata quando ammette un’unica soluzione.

Esempio:
£$ \frac{5}{2}x = 5 $£ ha un’unica soluzione, £$ x = 2 $£. È un’equazione determinata.

Un’equazione è indeterminata se ha infinite soluzioni: qualunque valore sostituiamo al posto dell’incognita, l’uguaglianza è sempre verificata. Sono equazioni indeterminate le identità che contengono un’incognita.

Esempio:
£$ 5x = 5x $£ è un’identità, quindi è sempre verificata, qualunque sia il valore di £$ x $£.
Nel risolvere un’equazione, riconosciamo che è indeterminata quando arriviamo ad avere una situazione di questo tipo: £$ 0x = 0 $£. Un numero qualsiasi moltiplicato per £$ 0 $£ dà sempre £$ 0 $£ come risultato: è un’equazione con infinite soluzioni.

Un’equazione è impossibile se non ha nessuna soluzione. Non riusciamo a trovare un valore che, sostituito all’incognita, verifica l’uguaglianza.

Esempio:
£$ 2x = 2x+3 $£ è un’equazione impossibile. Non riusciamo a trovare un numero che, sostituito all’incognita £$ x $£, renda vera questa uguaglianza.

Riconosciamo un’equazione impossibile quando ritroviamo una situazione di questo tipo: £$ 0x = 13 $£, cioè l’incognita moltiplicata per £$ 0 $£ uguale ad un numero diverso da £$ 0 $£. Sappiamo che un numero moltiplicato per £$ 0 $£ dà sempre £$ 0 $£ come risultato, quindi è impossibile trovare un numero che, moltiplicato per £$ 0 $£, dia un risultato diverso.

È facile riconoscere quali soluzioni ha un’equazione ridotta in forma normale. Aiutati con questo schema!