Numeri complessi in forma algebrica nel piano di Gauss
Finora ti hanno sempre detto che non esistono le radici dei numeri negativi. Ora scoprirai che si possono trovare! Come? Introducendo un nuovo insieme di numeri: l’insieme dei numeri complessi £$\mathbb{C}$£!
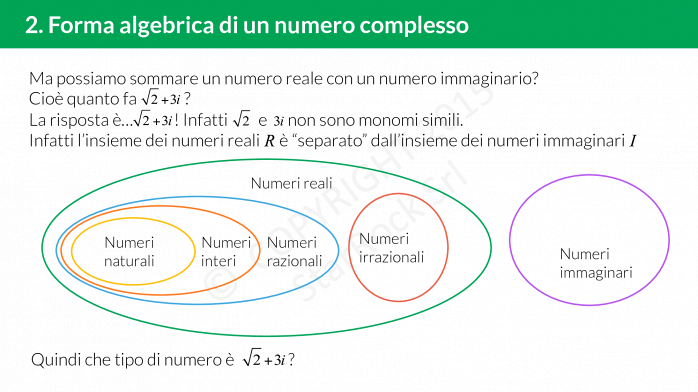
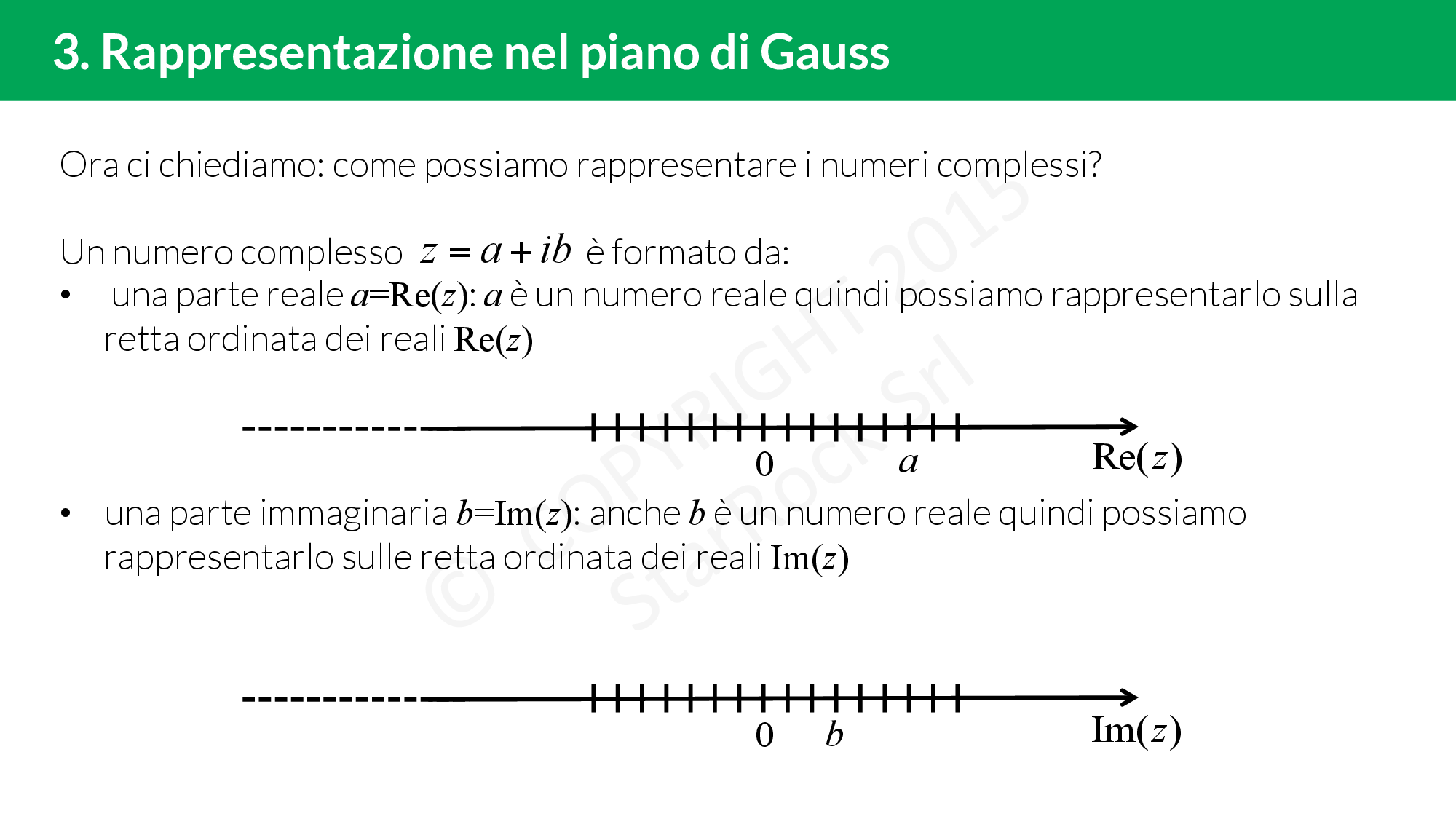
I numeri complessi possono essere espressi nella forma forma algebrica £$a+ib$£ dove £$a$£ e £$b$£ sono numeri reali e £$i$£ è l’unità immaginaria, cioè un numero che soddisfa l’equazione £$i^2=-1$£.
£$a$£ viene chiamata parte reale e £$ib$£ parte immaginaria, infatti un numero reale moltiplicato per l’unità immaginaria £$i$£ viene chiamato numero immaginario.
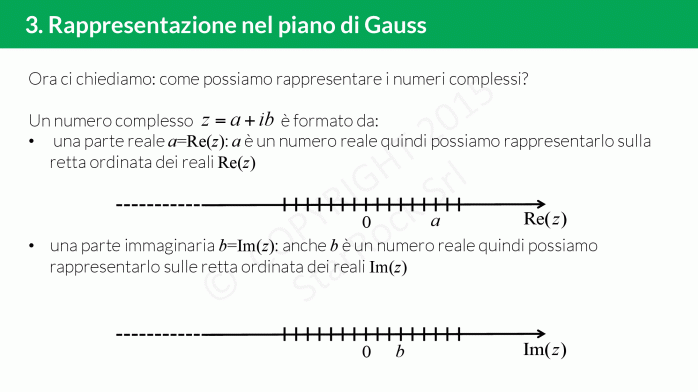
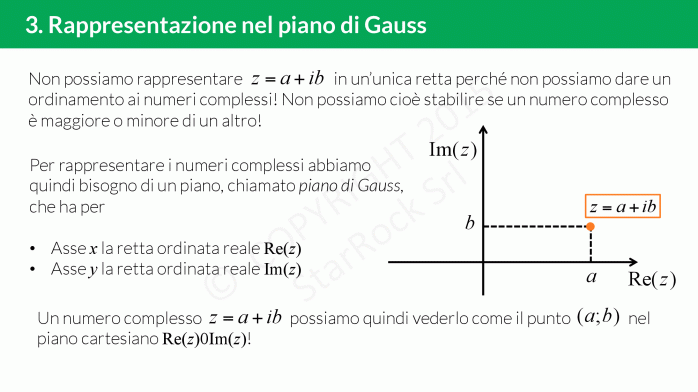
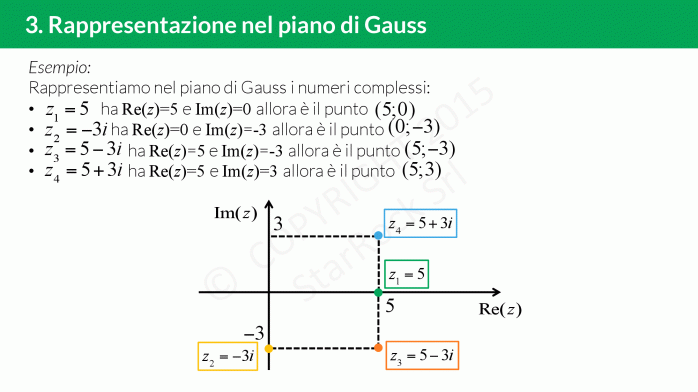
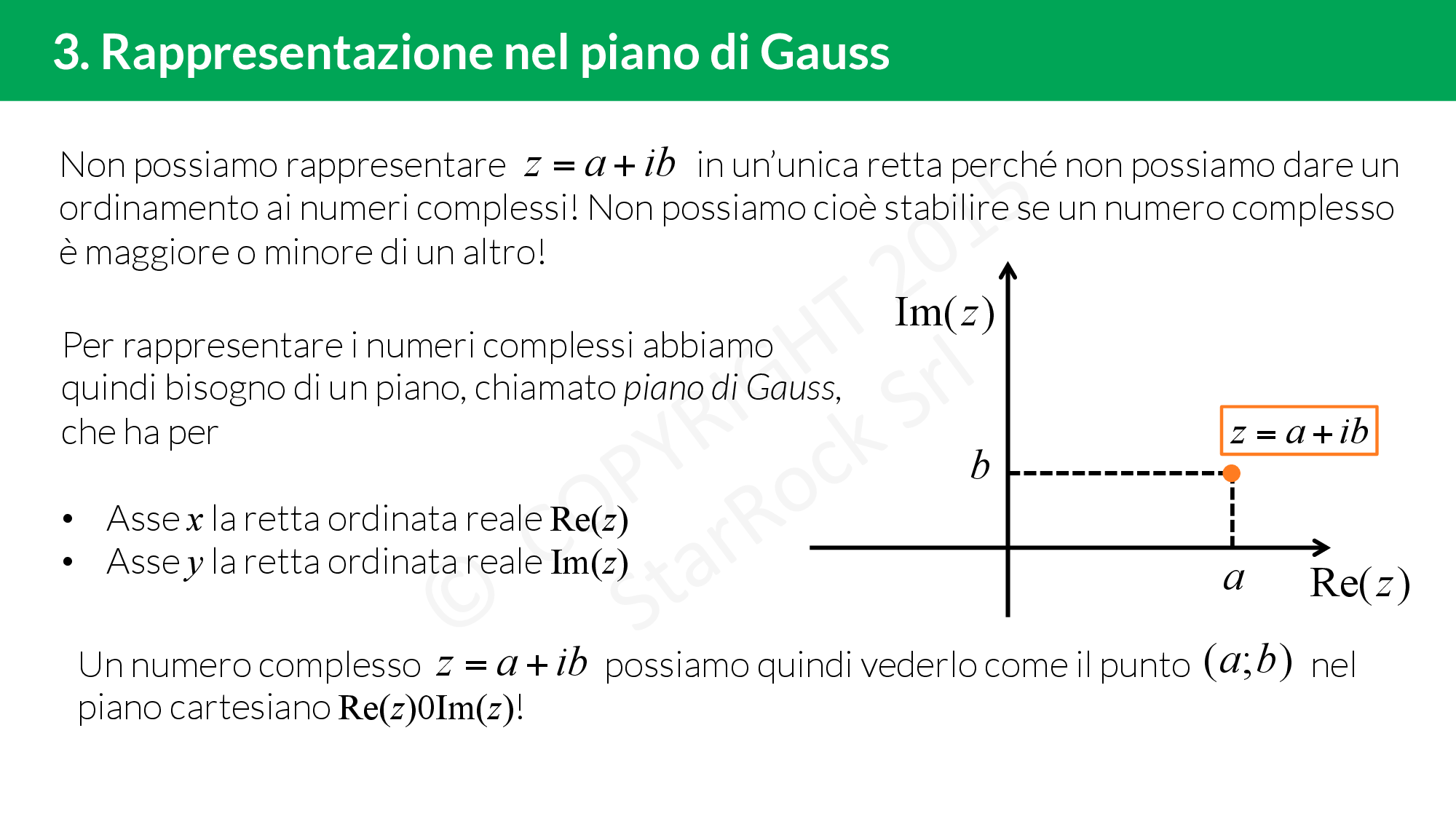
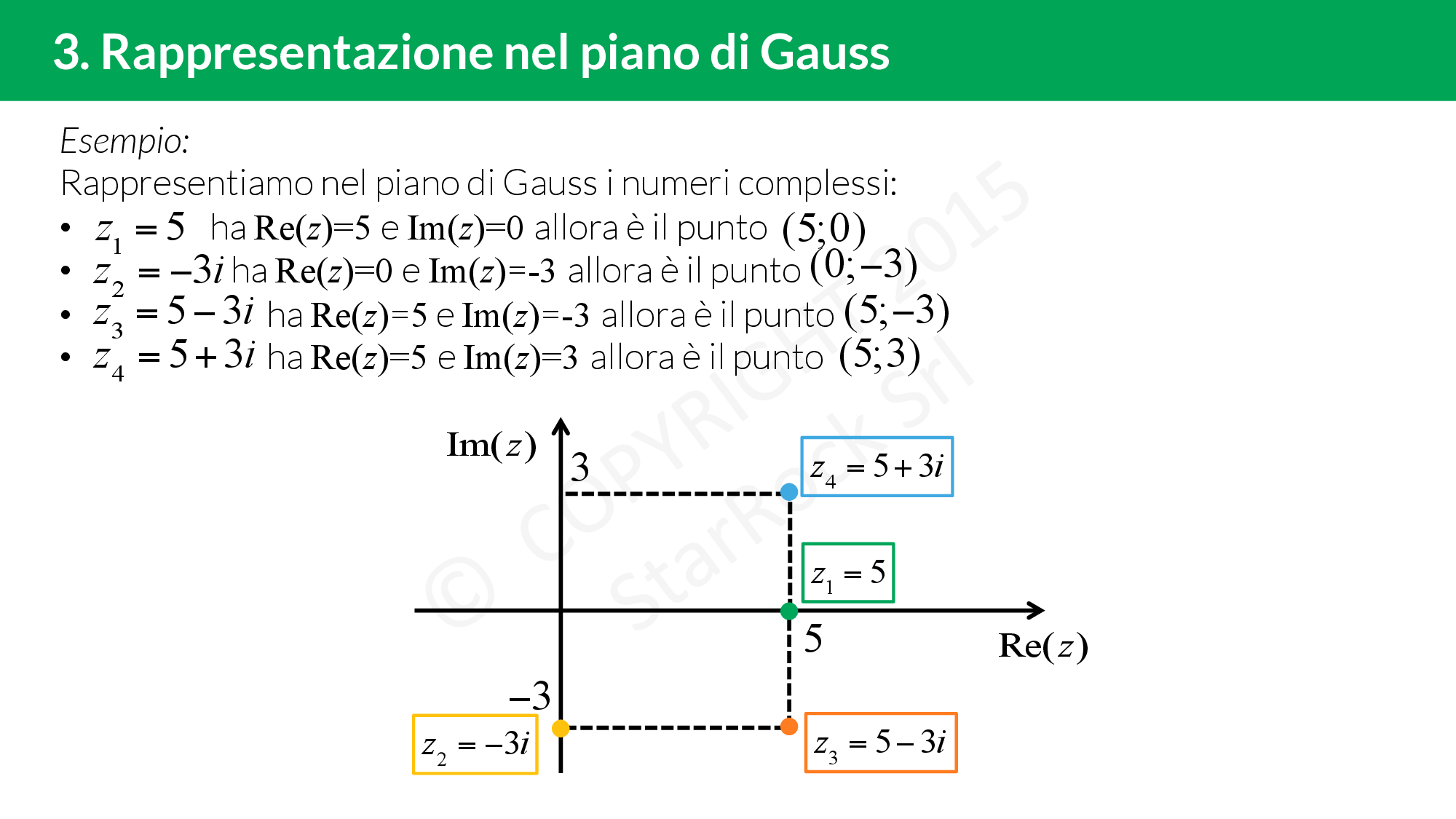
In questa lezione vedrai anche che i numeri complessi non possono essere in corrispondenza biunivoca con la retta poichè non è possibile dire se un numero complesso è più grande di un’altro. Quello che si può fare è associare al numero complesso £$a+ib$£ il punto £$(a; b)$£ nel piano, detto piano di Gauss: sull’asse delle ascisse metterai la parte reale e su quello delle ordinate la parte immaginaria.
Scoprirai anche come fare le principali operazioni con i numeri complessi scritti in forma algebrica!
- Cosa sono i numeri immaginari
- Forma algebrica dei numeri complessi
- Storia dei numeri complessi
- Rappresentazione sul piano di Gauss
- Esercizi svolti sui numeri complessi
Cosa sono i numeri immaginari
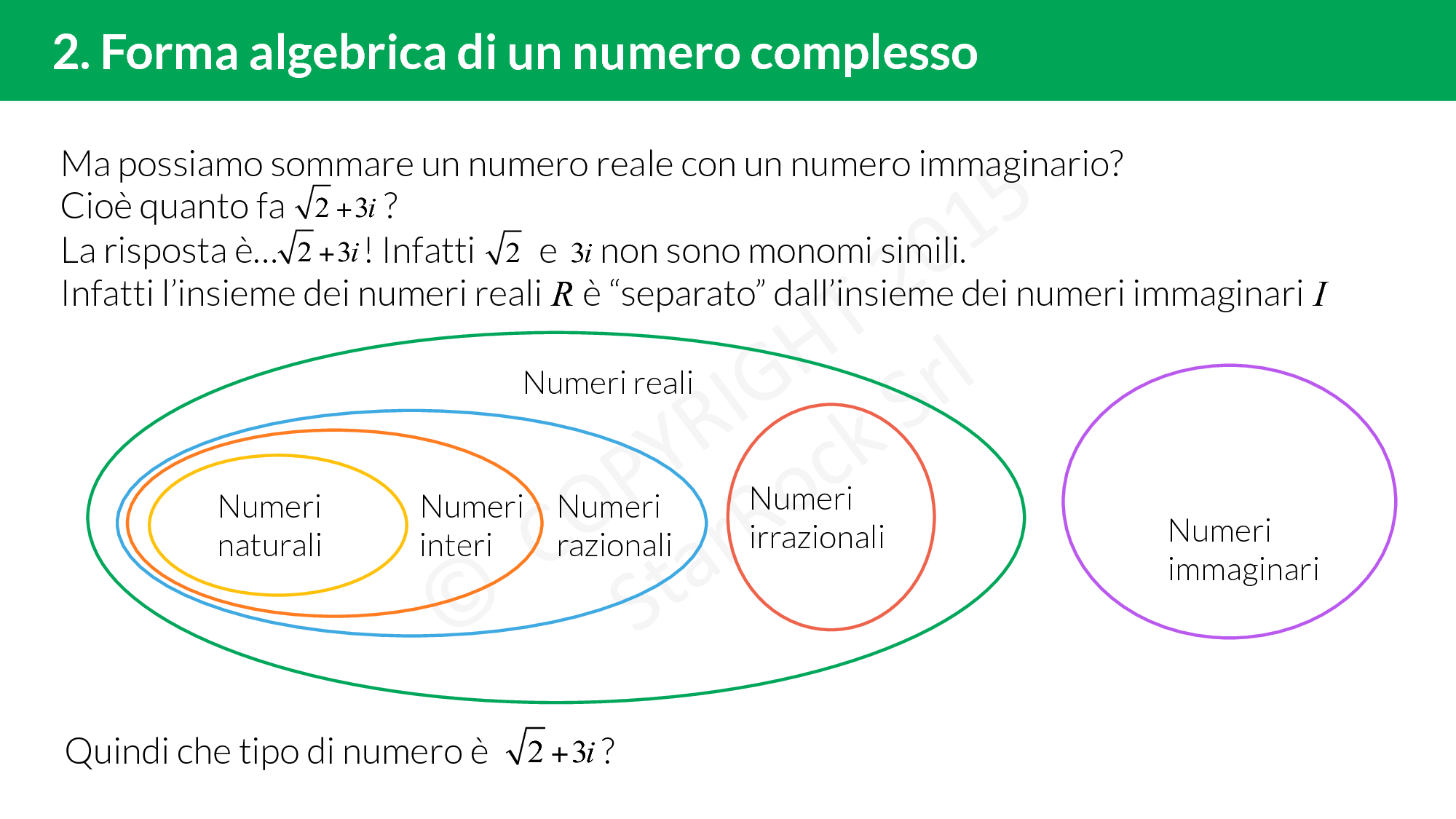
Finora, tutti i numeri che hai visto sono numeri reali, appartenenti all’insieme £$\mathbb{R}$£. Ma ci viene in mente una domanda: è possibile trovare una soluzione all’equazione £$x^2+1=0$£?
In teoria le soluzioni sono £$x=\pm \sqrt{-1}$£ che però sappiamo non essere numeri reali (infatti non esiste la radice quadrata di un numero negativo).
Se però definiamo un nuovo numero tale che elevato a quadrato dia £$-1$£ il gioco è fatto!
Allora chiamiamo £$i$£ quel numero tale che £$i^2=-1$£. Questo numero è chiamato unità immaginaria.
Quindi ora possiamo dire che l’equazione £$x^2+1=0$£ ha come soluzione £$\pm i$£.
Forma algebrica dei numeri complessi
Quanto fa un numero reale più un numero immaginario? Un numero complesso!
I numeri complessi sono tutti i numeri che sono somma di un numero reale è un numero immaginario, cioè hanno la forma $$a+ib$$ dove £$a,b \in \mathbb{R}$£ e £$i$£ è la nostra unità immaginaria.
Questa è la rappresentazione algebrica di un numero complesso.
Storia dei numeri complessi

Ma da dove vengono i numeri complessi?
Leggi la storia dei numeri complessi, che va da Cardano a Bombelli, fino ad arrivare al grande Eulero. Fu lui il primo a usare la lettera £$i$£ per rappresentare l’unità immaginaria!
Rappresentazione sul piano di Gauss
Ora che hai visto cosa sono i numeri complessi, dovrebbe venirti in mente una domanda: esiste un modo per rappresentarli graficamente?
Ovviamente la risposta è sì! E chi se non il grande Gauss ci poteva dare una mano?
I numeri complessi infatti si rappresentano sul piano di Gauss, che non è altro che un piano con due assi (come quello cartesiano) dove l’ascissa è la parte reale del numero mentre l’ordinata è la parte immaginaria.
Esercizi svolti sui numeri complessi
Testo degli esercizi:

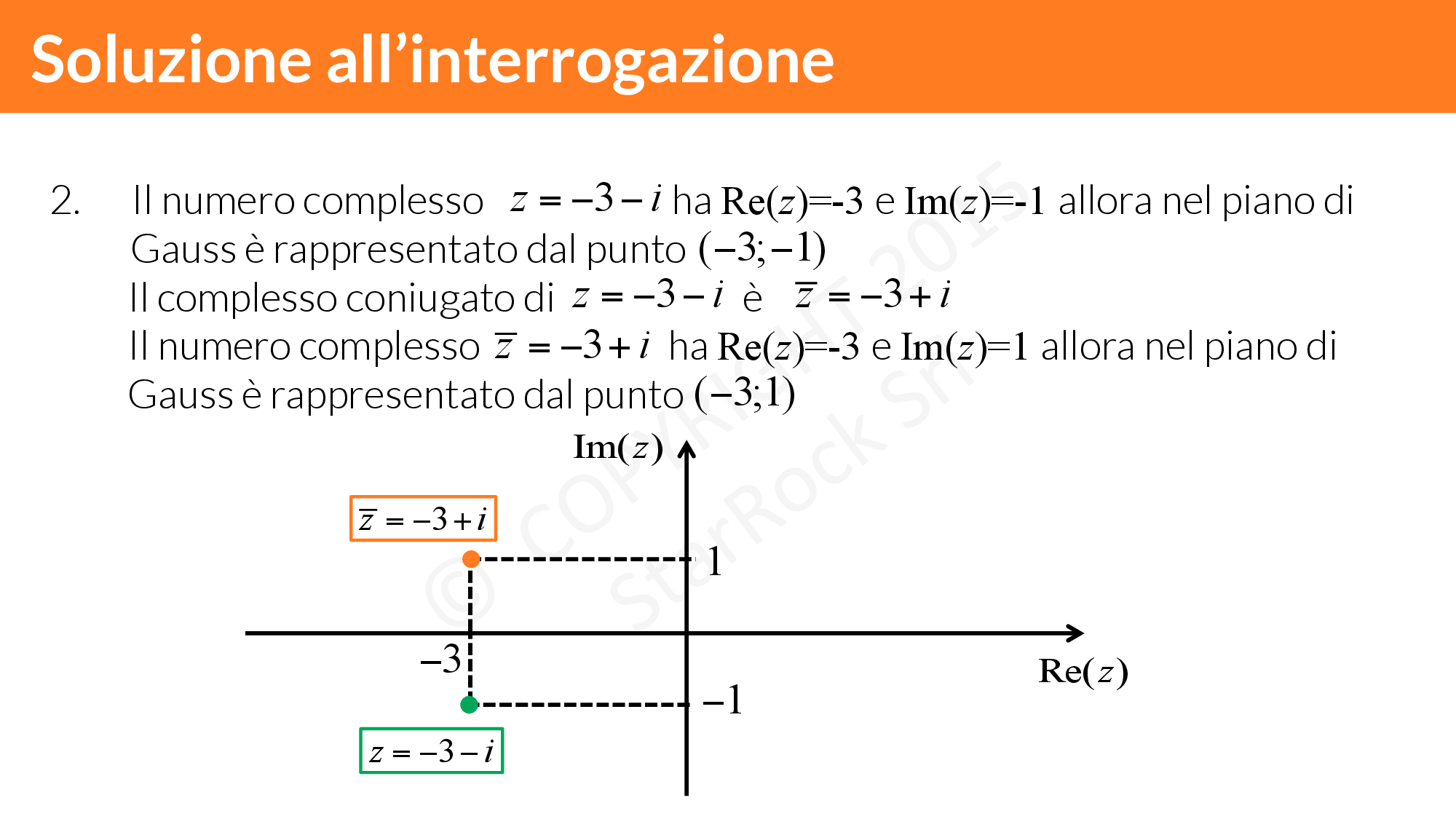
Soluzione degli esercizi:
Ora che hai visto cosa sono i numeri complessi e come fare le operazioni con i numeri complessi, verifica se hai capito tutto provando a svolgere questi esercizi. Se hai dubbi, puoi trovare anche la soluzione e confrontarla con il tuo ragionamento!