Formule goniometriche degli angoli associati
Gli angoli associati sono due angoli che hanno il loro vertice e un lato in comune. Solitamente si tratta di angoli formanti uno stesso sistema geometrico, come ad esempio angoli consecutivi, angoli complementari o angoli supplementari.
Gli angoli associati sono particolarmente utili nel contesto della geometria e della trigonometria per stabilire relazioni tra angoli e risolvere problemi geometrici. Quali sono le loro formule goniometriche? Scoprilo nelle tabelle sugli angoli associati: troverai seno coseno tangente e cotangente di angoli opposti, complementari, supplementari ed esplementari.
Conoscere le formule degli angoli associati ti permetterà di risolvere anche le espressioni complesse con le funzioni goniometriche. In questa lezione imparerai:
- Definizioni degli angoli associati: angoli opposti, esplementari, supplementari, angoli la cui differenza è 180°, complementari, angoli la cui somma è 90°, angoli la cui somma o differenza è 270°;
- Angoli opposti ed esplementari: formule goniometriche con relativa dimostrazione;
- Angoli supplementari o la cui differenza è 180°: formule con relativa dimostrazione;
- Angoli complementari o la cui differenza è 90°: formule con relativa dimostrazione;
- Angoli la cui somma o differenza è 270°: formule con relativa dimostrazione.
Usa le tabelle qui sotto per memorizzare tutte le formule degli angoli associati che ti serviranno per svolgere gli esercizi!
- Tabelle delle formule goniometriche
- Formule goniometriche degli angoli associati
- Angoli opposti e angoli esplementari: definizione
- Altre formule goniometriche degli angoli
- Ripassa per l'interrogazione sugli angoli associati
Tabelle delle formule goniometriche
Formulario 1
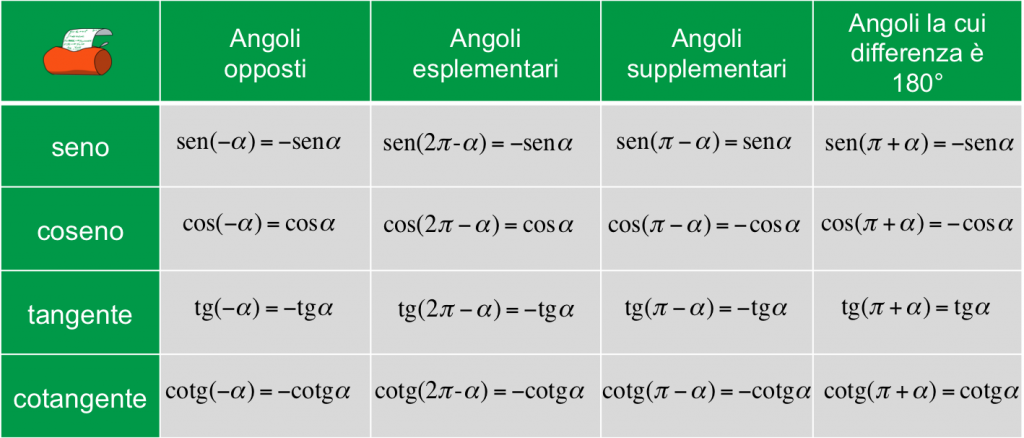
Formulario 2

Riassumiamo nelle tabelle le formule degli angoli associati che devi ricordarti.
- Opposti, se sono congruenti e orientati in senso opposto.
- Esplementari, se la loro somma è 360°, cioè £$2\pi$£.
- Supplementari, se la loro somma è 180°, cioè £$\pi$£.
- Angoli la cui differenza è 180°, cioè £$\pi$£.
- Complementari, se la loro somma è 90°, cioè £$\frac{\pi}{2}$£.
- Angoli la cui differenza è 90°, cioè £$\frac{\pi}{2}$£.
- Angoli la cui somma o differenza è 270°.
Tutte le formule si dimostrano ragionando sulle simmetrie della circonferenza goniometrica.
Formule goniometriche degli angoli associati
Le formule goniometriche degli angoli associati sono importanti perché ti permettono di velocizzare i calcoli. Infatti, dalla definizione delle funzioni goniometriche, i valori che queste funzioni assumono per alcuni angoli sono facilmente ricavabili.
Angoli opposti e angoli esplementari: definizione
Ecco le prime formule goniometriche, relative:
- agli angoli opposti, cioè angoli uguali in valore assoluto ma di segno opposto
- agli angoli esplementari, la cui somma è £$2\pi$£.
Grazie a queste proprietà delle funzioni goniometriche, potrai risolvere e semplificare di molto le espressioni e le equazioni con funzioni goniometriche!
Altre formule goniometriche degli angoli
- Angoli supplementari o la cui differenza è 180°
- Angoli complementari o la cui differenza è 90°
- Angoli la cui somma o differenza è 270°
In queste tre lezioni, troverai tutte le formule goniometriche relative a:
- angoli supplementari o la cui differenza è £$\pi$£
- angoli complementari o la cui differenza è £$\frac{\pi}{2}$£
- angoli la cui somma o differenza è £$\frac{3}{2}\pi$£
C’è un modo per imparare queste formule? Studiandole a memoria! In realtà il modo migliore è capirle disegnando sempre la circonferenza goniometrica e poi ragionando sui valori delle funzioni negli angoli che ci interessano.
Ripassa per l’interrogazione sugli angoli associati

Ecco alcuni esercizi per imparare a maneggiare le formule goniometriche degli angoli associati.
Ti permetteranno di fare bella figura all’interrogazione!






















