Equivalenze con le misure: tre problemi svolti
Le misure di grandezza sono molto importanti perchè ci aiutano a capire quanto è grande, lungo o pesante qualcosa. Ad esempio, possiamo misurare la lunghezza di una matita, il peso di una mela o il volume di una bottiglia d’acqua. A volte, dobbiamo trasformare queste misure in altre unità, e questo si chiama fare equivalenze. Per esempio, possiamo convertire metri in centimetri o chilogrammi in grammi. Imparare a fare equivalenze è molto utile e divertente, perché ci aiuta a confrontare e capire meglio le cose che ci circondano!
Le misure di grandezza non hanno più segreti! Prova a risolvere i problemi più difficili applicando le equivalenze. Ripassa il metro, il chilogrammo e il litro e prova a trovare la soluzione!
Ecco tre problemi svolti. Segui tutti i passaggi per capire come risolvere un problema sulla lunghezza, uno sulla massa e uno sulla capacità.
Preparati al meglio!
- Risolvi un problema sulla lunghezza
- Risolvi un problema sulla massa
- Risolvi un problema sulla capacità
Risolvi un problema sulla lunghezza
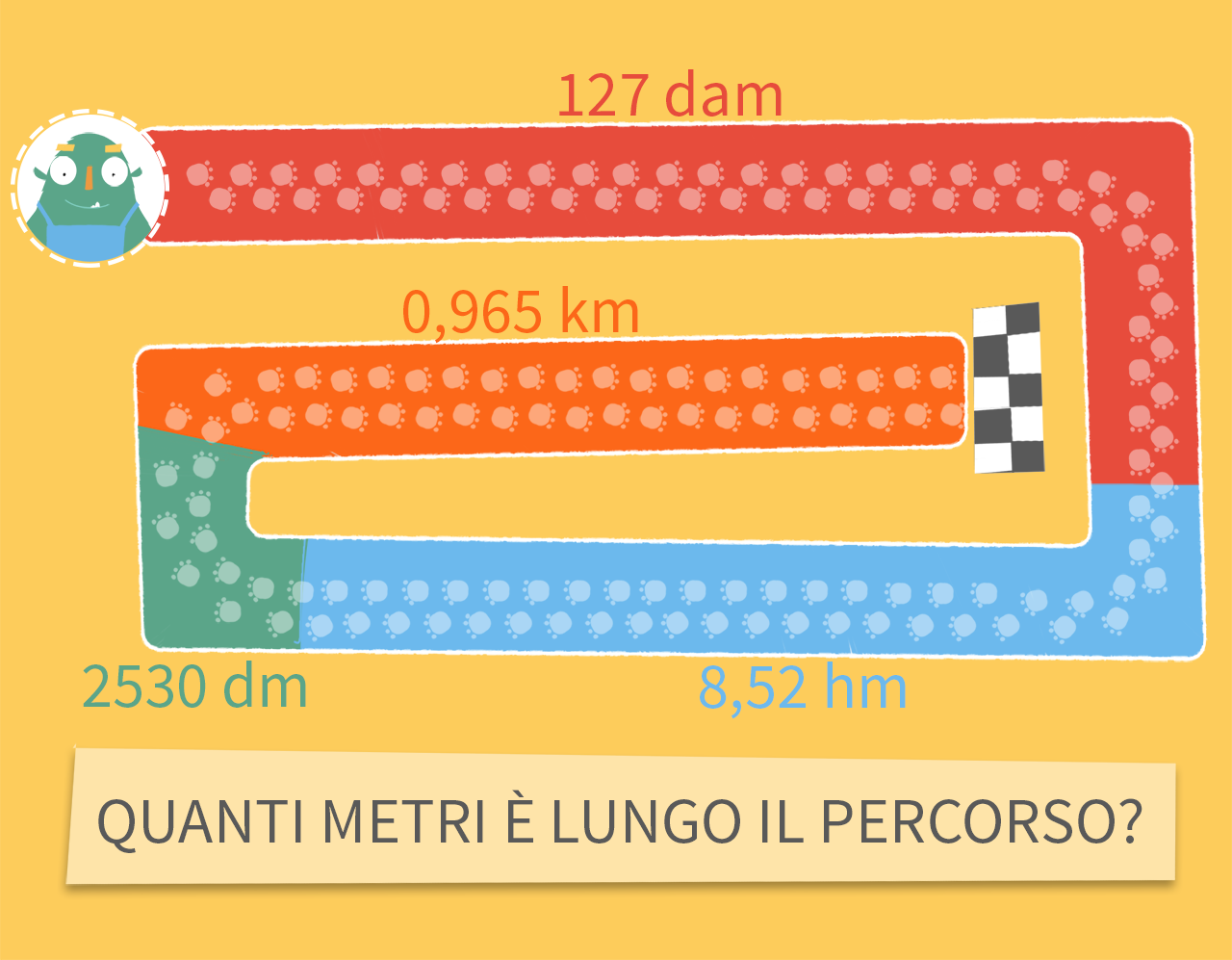
DATI:
rosso £$ = 127 \text{ dam} $£
blu £$ = 8{,}52 \text{ hm} $£
verde £$ = 2530 \text{ dm} $£
arancione £$ = 0{,}965 \text{ km} $£
DOMANDA: lunghezza totale del percorso in metri = ?
Per calcolare la lunghezza totale del percorso dobbiamo sommare le lunghezze delle quattro parti: £$ 127 \text{ dam} + 8{,}52 \text{ hm} + 2530 \text{ dm} + 0{,}965 \text{ km} $£
Attenzione! Per sommare queste lunghezze dobbiamo usare la stessa unità di misura! La domanda ci chiede di calcolare la lunghezza totale del percorso in metri, allora conviene convertire ciascuna lunghezza in metri.
Per esempio, convertiamo £$ 127 \text{ dam} $£ in metri: basta moltiplicare per £$10$£! £$ 127 \text{ dam} = 127 \times 10 \text{ m} = 1270 \text{ m} $£
Procediamo nello stesso modo anche per le altre misure.
- £$ 8{,}52 \text{ hm} = 8{,}52 \times 100 \text{ m} = 852 \text{ m} $£
- £$ 2530 \text{ dm} = 2530 : 10 \text{ m} = 253 \text{ m} $£
- £$ 0{,}965 \text{ km} = 0{,}965 \times 1000 \text{ m} = 965 \text{ m} $£
E ora sommiamo!
$$ 1270 \text{ m} + 852 \text{ m} + 253 \text{ m} + 965 \text{ m} = 3340 \text{ m} $$
Il percorso di allenamento è lungo in totale £$3340 \text{ m} $£.
IDEA! Possiamo anche svolgere lo stesso problema compilando una semplice tabellina. Scegli tu il metodo che preferisci!
begin{array}{c|c|c||c||c|c} text{km}&text{hm}&text{dam}&text{m}&text{dm}&\ 1&2&7&&&+\ &8&5&2&&+\ &2&5&3&0&+\ 0&9&6&5&&=\ hline 3&3&4&0&text{m} end{array}
Risolvi un problema sulla massa

DATI:
peso totale £$ = 175 \text{ kg} $£
altezza tavoletta £$ = 7 $£ quadretti
larghezza tavoletta £$ = 5 $£ quadretti
DOMANDA: peso di un quadretto in centigrammi = ?
Per calcolare il peso di ciascun quadretto abbiamo bisogno di conoscere quanti quadretti ci sono nell’intera tavoletta. La tavoletta è alta £$ 7 $£ quadretti e larga £$ 5 $£. In totale allora ci sono £$ 7 \times 5 = 35 $£ quadretti.
Ora basta dividere il peso totale per il numero di quadretti.
$$ 175 \text{ kg} : 35 = 5 \text{ kg} $$
Ciascun quadretto pesa £$ 5 \text{ kg} $£!!!
Ma non abbiamo finito… Dobbiamo convertire il peso in centigrammi. Per passare da £$ \text{ kg} $£ a £$ \text{ cg} $£ dobbiamo moltiplicare per… £$ 100 \, 000 $£!
$$ 5 \text{ kg} = 5 \times 100 \, 000 = 500 \, 000 \text{ cg} $$
Ogni quadretto pesa £$ 500 \, 000 \text{ cg} $£. Una scorpacciata di cioccolato!
Risolvi un problema sulla capacità

DATI:
Etichetta blu £$ = 17 \text{ l} $£
Etichetta gialla £$ = 250 \text{ ml} $£
Etichetta bianca £$ = 0{,}015 \text{ hl} $£
DOMANDA:
Etichetta contenitore grande = ?
Etichetta contenitore medio = ?
Etichetta contenitore piccolo = ?
Per scegliere l’etichetta giusta per ciascun contenitore dobbiamo confrontare le tre misure di capacità e metterle in ordine: dalla più grande alla più piccola.
Attenzione! Per confrontare queste capacità dobbiamo usare la stessa unità di misura! Non facciamoci ingannare dai numeri… Possiamo scegliere quella che ci piace di più o che sembra più comoda, per esempio il litro!
La misura sull’etichetta blu è già espressa in litri! Perfetto! Possiamo andare avanti e convertire le altre due misure.
- £$ 0,015 \text{ hl} = 0{,}015 \times 100 \text{ l} = 1{,}5 \text{ l} $£
- £$ 250 \text{ ml} = 250 : 1000 \text{ l} = 0{,}25 \text{ l} $£
E ora non ci resta che confrontare le tre misure! £$ 0{,}25 \text{ l} $£ è la più piccola, £$ 17 \text{ l} $£ è la più grande.
$$ 17 \text{ l} > 1{,}5 \text{ l} > 0{,}25 \text{ l} $$
L’ordine corretto, dalla più grande alla più piccola è:
- etichetta blu
- etichetta bianca
- etichetta gialla
IDEA! Ricorda che puoi sempre rappresentare le misure in una tabella e poi confrontarle! Scegli tu il metodo che preferisci!
begin{array}{c|c||c||c|c|c} text{hl}&text{dal}&text{l}&text{dl}&text{cl}&text{ml}\ 0&0&1&5&&\ &1&7&&&\ &&&2&5&0\ end{array}
