Il metro: l'unità di misura della lunghezza
Il metro, simbolo m, è l’unità di base della lunghezza nel Sistema Internazionale di Unità (SI), ed è una delle unità di misura fondamentali e ampiamente utilizzate in scienza, ingegneria e vita quotidiana.
Definito originariamente come un dieci milionesimo della distanza dal polo Nord all’Equatore lungo il meridiano che passa per Parigi, il metro ha subito varie ridefinizioni nel corso degli anni per migliorarne la precisione e l’affidabilità, riflettendo l’evoluzione della tecnologia di misurazione e la comprensione scientifica.
La definizione attuale del metro, adottata dalla 17ª Conferenza Generale dei Pesi e delle Misure nel 1983, si basa sulla velocità della luce nel vuoto, un parametro fisico universale e costante. Secondo questa definizione, un metro è la distanza percorsa dalla luce nel vuoto in un intervallo di tempo di 1/299.792.458 di secondo.
Il metro è il pilastro su cui si costruiscono tutte le altre misure di lunghezza e distanza nel Sistema Internazionale, servendo come riferimento per derivare unità più grandi e più piccole. Quale unità di misura è più adatta per misurare la lunghezza di una strada? Scopri i multipli del metro: decametro, ettometro, chilometro. E cosa è più utile per misurare la lunghezza di una pagina di quaderno? Scopri i sottomultipli del metro: decimetro, centimetro, millimetro. Impara a passare da un’unità di misura all’altra con le equivalenze.
Vediamole insieme.
- Un po' di storia: come è nato il metro?
- L'unità di misura convenzionale per la lunghezza: il metro
- Multipli e sottomultipli del metro
- Come scomporre le misure date in metri
- Come fare le equivalenze con multipli e sottomultipli del metro
- Giochi per stimare la lunghezza di un oggetto
- Esercizi da svolgere sul metro
- Scheda di esercizi sulle equivalenze del metro
Un po’ di storia: come è nato il metro?
Quella matita è lunga una spanna. Carlo dista £$ 7 $£ passi da Lorenzo.
Ma con queste unità di misura, come facciamo a capire la vera lunghezza di un oggetto o la vera distanza tra due cose? Le nostre mani non sono tutte uguali, nemmeno i nostri passi: serve un’unità di misura che sia valida per tutti nello stesso modo!
Gli antichi utilizzavano unità di misura diverse a seconda delle loro esigenze e degli strumenti a loro disposizione. Finalmente con la rivoluzione francese e l’avvento del metodo scientifico, si arrivò ad un’unità di misura unica: il metro, la decimilionesima parte della distanza tra l’equatore e il polo nord, misurata sul meridiano terrestre passante per Parigi. Il campione di metro è una barra di platino-iridio conservata a Parigi, all’Ufficio internazionale dei pesi e delle misure. Ma visto che la materia con il tempo si deforma, nel £$ 1983 $£ si diede un’altra definizione più accurata: un metro è la distanza percorsa dalla luce nel vuoto in un intervallo di tempo di £$ \frac{1}{299 \ 792 \ 458} $£ secondi.
L’unità di misura convenzionale per la lunghezza: il metro

Per misurare la lunghezza di un oggetto abbiamo imparato ad utilizzare le parti del nostro corpo, oppure degli oggetti tutti uguali scelti come unità di misura. Per essere sicuri però che le nostre misure siano chiare a tutti, occorre un’unità di misura uguale per tutti, in tutto il mondo.
Per misurare la lunghezza utilizziamo il metro.
L’unità di misura fondamentale della lunghezza è il metro. Il campione del metro è costituito da una barra di platino-iridio conservato all’ufficio internazionale dei pesi e delle misure a Parigi.
Come tutte le unità di misura, il metro ha i suoi multipli (decametro, ettometro, chilometro) e sottomultipli (decimetro, centimetro, millimetro).
Dal Sistema Internazionale delle unità di misura, vediamo che il metro si indica con una lettera minuscola, la £$ \text{m} $£. Ma ci sono dei simboli anche per i multipli e i sottomultipli:
- £$ \text{km} = $£ chilo-metro £$ = 1000 \text{ m} $£
- £$ \text{hm} = $£ etto-metro £$ = 100 \text{ m} $£
- £$ \text{dam} = $£ deca-metro £$ = 10 \text{ m} $£
- £$ \text{m} = $£ metro
- £$ \text{dm} = $£ deci-metro £$ = \frac{1}{10} \text{ m} $£
- £$ \text{cm} = $£ centi-metro £$ = \frac{1}{100} \text{ m} $£
- £$ \text{mm} = $£ milli-metro £$ = \frac{1}{1000} \text{ m} $£
Esistono anche altre unità di misura che vengono utilizzate per la lunghezza. Per esempio le miglia, dal latino milia passum, che significa migliaia di passi: erano utilizzate dagli antichi romani e sono ancora utilizzate nei paesi anglosassoni, per indicare le distanze aeree e navali. Un’altra unità di misura per la lunghezza che si utilizza ancora è lo yard: lo sentiamo nominare molte volte durante una partita di football americano. E ti è mai capitato di comprare un televisore? Le dimensioni dello schermo sono indicate in pollici: è la misura della diagonale dello schermo. Questa unità di misura si utilizza molto per indicare il diametro di tubi o anche dei cerchioni delle auto e delle moto: un pollice corrisponde a circa £$ 2,54 \text{ cm} $£.
Multipli e sottomultipli del metro
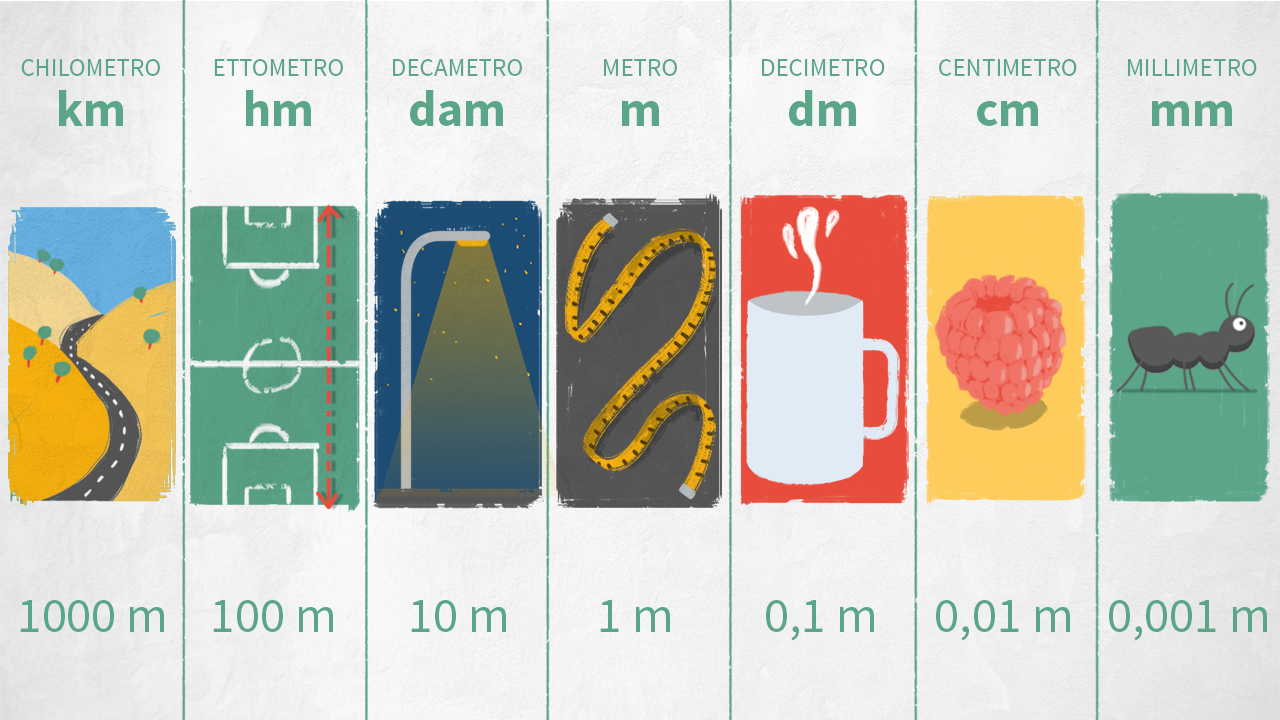
Per misurare certi oggetti, un metro è troppo lungo. Per questo esistono unità di misura che sono 10, 100 o 1000 volte più piccole: i sottomultipli del metro. Sono il decimetro, il centimetro e il millimetro.
Ma di quanti metri avremmo bisogno per misurare la strada per arrivare a scuola? Per questo esistono unità di misura 10, 100 o 1000 volte più grandi: i multipli del metro. Sono il decametro, l’ettometro e il chilometro.
La lunghezza degli oggetti si misura utilizzando unità di misura diverse. È più comodo misurare la lunghezza di un foglio di quaderno in metri o in centimetri? E invece come misureresti la lunghezza di una stanza? Oppure l’altezza del palazzo della tua scuola?
Possiamo misurare le diverse cose con unità di misura differenti, ma possiamo sempre confrontarle perché si tratta di lunghezze. Per confrontarle più facilmente, conviene renderle tutte equivalenti, cioè scrivere tutte le misure in metri, oppure tutte in centimetri, oppure tutte in chilometri… E così via.
Ma come si fa? Utilizziamo le equivalenze! Sono delle uguaglianze tra due espressioni con un’unità di misura diversa: riusciamo a scrivere la stessa quantità in due modi diversi.
Partiamo da £$ 1 \text{ m} $£ e troviamo tutte le misure equivalenti. Ogni passaggio che facciamo salendo, quindi verso i multipli del metro, dividiamo per £$ 10 $£. Come passiamo da metri a chilometri? Tre passaggi, quindi dividiamo per £$ 10 $£ tre volte, cioè dividiamo per £$ 10 \cdot 10 \cdot 10 = 1000 = 10^3 $£. Infatti il prefisso chilo significa proprio mille. Per passare invece da un’unità di misura a una sua sottomultipla dobbiamo scendere: ogni passaggio che facciamo verso il basso, moltiplichiamo per £$ 10 $£. Come passiamo da ettometri a centimetri? Sono quattro passaggi, quindi moltiplichiamo per £$ 10 $£ quattro volte, cioè moltiplichiamo per £$ 10 \, 000 = 10^4 $£.
Come scomporre le misure date in metri
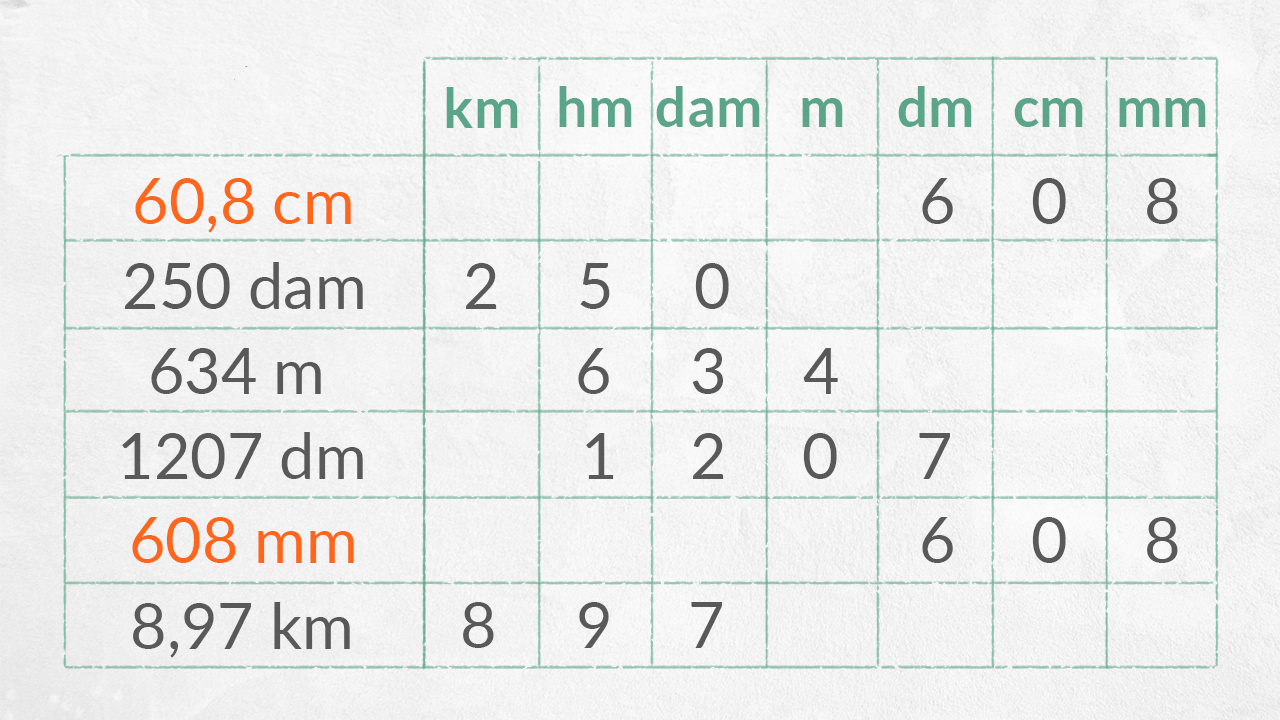
Ogni unità di misura è 10 volte più piccola di quella alla sua sinistra nella tabella, mentre è 10 volte più grande di quella alla sua destra nella tabella.
Due misure sono equivalenti se, dopo la scomposizione, sono uguali. Possiamo esprimere la stessa lunghezza utilizzando unità di misura diverse!
L’unità di misura che segue il numero si riferisce alle unità.
Esempio: 75 hm = 7 km + 5 hm.
Come fare le equivalenze con multipli e sottomultipli del metro
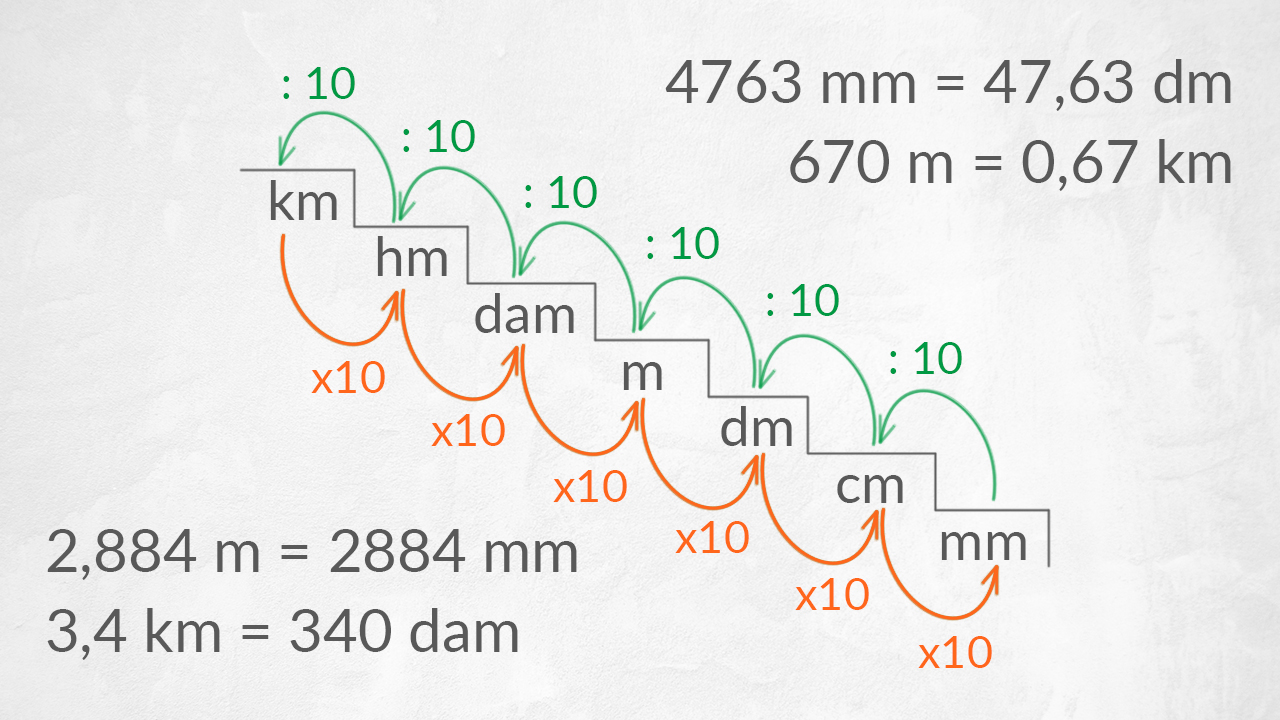
Come facciamo a convertire le unità di misura in unità di misura equivalenti?
Come possiamo passare da metri a centimetri? E da chilometri a metri?
Prendiamo la tabella delle unità di misura e trasformiamola in una scaletta: sulla cima troviamo i chilometri e alla base della scala ci sono i millimetri.
Ogni volta che saliamo la scalinata, facciamo più fatica… Quindi dividiamo per 10 ad ogni gradino in salita. Se scendiamo la scalinata, invece, andiamo più velocemente… Moltiplichiamo per 10 ad ogni gradino in discesa!
Giochi per stimare la lunghezza di un oggetto
Iniziamo con qualche esercizio per imparare a capire la misura degli oggetti anche senza utilizzare gli strumenti di misura. Si dice, appunto, stimare: ovvero fare una buona ipotesi o una valutazione approssimativa di qualcosa quando non possiamo conoscere il valore esatto.
È come fare una previsione basata su quello che sappiamo. Ad esempio, se guardiamo un barattolo pieno di caramelle, possiamo stimare quanti ce ne sono dentro anche senza contarli uno per uno.
Stime bizzarre

Scarica la scheda con le istruzioni del gioco:
Stima e misura

Scarica la scheda con le istruzioni per il gioco:
Esercizi da svolgere sul metro
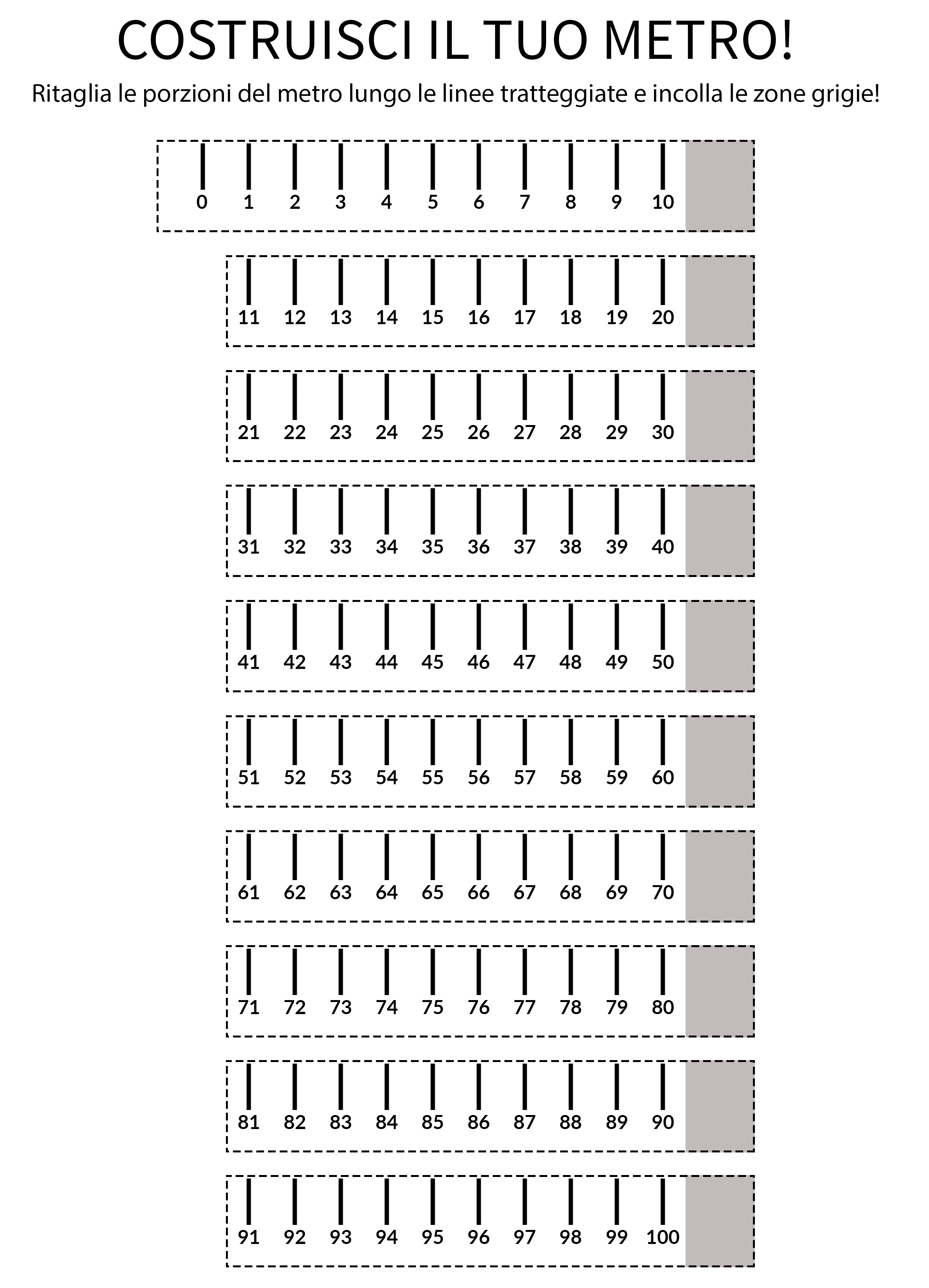
Iniziamo ad introdurre le unità di misura di lunghezza: il metro con i suoi multipli e sottomultipli.
Ogni bambino può costruire il suo metro personale! Scarica la scheda, stampa, ritaglia e incolla tutti i pezzi. Ogni bambino può personalizzare il proprio metro come preferisce. Ecco la scheda:
Una volta che i bambini hanno in mano il proprio metro, possiamo fare qualche ragionamento insieme: ogni pezzo del metro è un decimetro, ogni tacca è un centimetro. In questo modo possono vedere che 10 centimetri fanno un decimetro, 10 decimetri fanno un metro. Quanti centimetri servono per fare un metro? Iniziamo a parlare di equivalenze.

Un gioco per prendere confidenza con questa novità è il salto della rana. Sul pavimento posizionate un cartellone: sarà la nostro pista per il salto delle rane. Sul tabellone fate un bel metro, suddiviso in centimetri. Potete far partecipare i bambini: ognuno di loro può creare un decimetro suddividendo il foglio in 10 parti uguali, i 10 centimetri. Poi numerate tutti i pezzi e uniteli a formare il tabellone. In alternativa, potete utilizzare il metro costruito utilizzando l’altra scheda.
Ogni bambino realizza la sua rana da corsa: scarica qui la scheda con le istruzioni per costruire la rana! Una volta realizzato l’origami, seguendo le istruzioni, i bambini la possono decorare come meglio credono e prepararsi alla partenza. Prova a far saltare la rana: premi come indicato sulla scheda dal “push". Via! Inizia la gara di salto in lungo: quale rana arriverà più lontano? Misurate e confrontate le lunghezze dei salti delle rane.

Scarica la scheda con le istruzioni e realizzate la piantina della vostra classe:

Scarica la scheda con le istruzioni per il gioco:
Scheda di esercizi sulle equivalenze del metro

Qualche esercizio in più per allenarsi con problemini ed equivalenze! Scarica qui la scheda:
