L'addizione: come si fa e quali sono le sue proprietà
L’addizione è una delle quattro operazioni aritmetiche fondamentali. Questa operazione consiste nel combinare due o più numeri per ottenere una somma totale, ed è uno dei primi concetti matematici insegnati durante l’infanzia, sottolineando il suo ruolo fondamentale nella comprensione della matematica e delle sue applicazioni pratiche nella vita quotidiana. L’addizione è il mezzo attraverso il quale quantifichiamo il processo di unione di gruppi di oggetti, misuriamo le lunghezze combinate, calcoliamo il totale delle spese e risolviamo innumerevoli altri problemi pratici e teorici.
Le proprietà dell’addizione sono regole universali che descrivono come si comportano i numeri quando vengono sommati. Queste proprietà non solo facilitano la comprensione del processo di addizione, ma offrono anche una struttura per risolvere problemi matematici in modo più efficiente e intuitivo.
Una delle proprietà fondamentali dell’addizione è la proprietà commutativa, che afferma che l’ordine dei numeri sommati non influisce sul risultato finale. La proprietà associativa dell’addizione indica che quando si sommano tre o più numeri, il modo in cui i numeri vengono raggruppati non cambia la somma totale. Questa proprietà è particolarmente utile quando si lavora con espressioni algebriche complesse, poiché consente di modificare il raggruppamento dei termini senza alterare il valore dell’espressione.
La proprietà dell’elemento neutro, o proprietà dell’identità dell’addizione, stabilisce che l’aggiunta di zero a qualsiasi numero non cambia il valore di quel numero. Questa proprietà sottolinea il ruolo unico dello zero nell’aritmetica, agendo come un elemento neutro che non influisce sull’operazione di addizione.
Alla fine dell’articolo troverai tante schede pronte da utilizzare per fare esercizi sulle addizioni.
- I termini dell'addizione
- L'elemento neutro dell'addizione
- Proprietà associativa dell'addizione
- Proprietà dissociativa dell'addizione
- Proprietà commutativa dell'addizione
- Un esempio di addizione
- Addizioni fino a 100 e 1000
- Schede di esercizi con le addizioni
I termini dell’addizione
L’addizione è l’operazione che svolgiamo per aggiungere una quantità ad un’altra, cioè aggiungere un numero ad un altro.
Il segno aritmetico che indica l’addizione è il segno £$ + $£ che leggiamo più.
I due numeri che aggiungiamo uno all’altro sono gli addendi e sono separati dal segno £$ + $£. Possiamo scrivere, ad esempio, l’addizione £$ 5 + 7 $£, dove £$ 5 $£ e £$ 7 $£ sono i due addendi.
Quando parliamo di addizioni, le indichiamo anche come somme: questo perché il risultato di questa operazione si chiama somma o totale.
$$ 5 + 7 = 12 $$
il £$ 5 $£ e il £$ 7 $£ sono i due addendi, il £$ 12 $£ è la somma o il totale.
L’elemento neutro dell’addizione
Esiste un numero particolare che ha uno strano comportamento nelle addizioni. Si tratta dello £$ 0 $£.
Infatti se noi aggiungiamo £$ 0 $£ ad un numero qualsiasi, il risultato di questa somma è il numero stesso. Aggiungere £$ 0 $£ è come non aggiungere niente.
Diciamo quindi che lo £$ 0 $£ è l’elemento neutro dell’addizione.
$$ 86 + 0 = 0 + 86 = 86 $$
Proprietà associativa dell’addizione
Cosa significa proprietà associativa:
Come funziona la proprietà associativa:
Una proprietà dell’addizione è la proprietà associativa: se sostituiamo a due numeri la loro somma, il risultato non cambia.
Infatti l’aggettivo “associativa" deriva da “associare" che significa unire, mettere insieme due o più elementi. La proprietà associativa ti aiuta a semplificare i calcoli risolvendo prima le somme per te più facili.
Esempio: Risolviamo £$ 7 + 3 + 6 $£. Proviamo a sommare i primi 2 termini: £$ (7 + 3) + 6 = 10 + 6 = 16 $£. Anche se sommiamo prima gli ultimi 2 termini, otteniamo lo stesso risultato: £$ 7 + (3 + 6) = 7 + 9 = 16 $£.
Proprietà dissociativa dell’addizione
Infine, la proprietà dissociativa: la somma di due o più addendi non cambia se a uno di questi sostituiamo più numeri la cui somma sia uguale all’addendo sostituito.
Esempio: Risolviamo £$ 32 + 28 $£.
Diventa £$ 30 + 2 + 28 $£ rendendo più semplice l’addizione: £$ 2 $£ e £$ 8 $£ sono numeri amici!
Proprietà commutativa dell’addizione
Cosa significa proprietà commutativa:
Come funziona la proprietà commutativa:
L’addizione ha diverse proprietà. La proprietà commutativa dice che se cambiamo l’ordine degli addendi, il risultato non cambia!
Infatti l’aggettivo “commutativa" deriva da “commutare" che significa proprio scambiare due cose tra loro.
Esempio: £$ 5 + 3 $£ è uguale a fare £$ 3 + 5 $£. Il risultato è sempre £$ 8 $£
Tavola delle memorizzazioni
Il materiale a disposizione comprende:
- la tavola di posa: è rettangolare e suddivisa in quadrati tutti uguali 18 di larghezza e 12 di altezza;
- una scatola contenente 9 asticine blu, che costituiscono il primo addendo, e nove asticine rosse, che costituiscono il secondo addendo.
Un esempio di addizione
Per cominciare inventiamo un addizione, ad esempio 6 + 4.
Prendiamo l’asticina blu numero 6 e la mettiamo a sinistra, sulla tavola di posa. Successivamente prendiamo l’asticina rossa 4 e la mettiamo di fianco a quella blu.
Il risultato dell’addizione è subito visibile in alto sulla striscia di numeri orizzontale.
Come sommare 8+5
Proviamo con un altro esempio: 8 + 5.
Posiamo prima l’asticina blu del numero 8, poi quella rossa numero 5. Leggiamo subito il risultato in alto: 13.
La linea rossa permette di vedere quanto manca da 10 a 13.
Addizioni fino a 100 e 1000
Il calcolo tra decine non ha più segreti per te? Scopriamolo insieme.
Quando impariamo a fare addizioni fino a 100, ci esercitiamo a sommare numeri più piccoli, come ad esempio 45 + 35, che ci dà come risultato 80. Questo tipo di addizioni è utile per risolvere problemi quotidiani semplici, come sommare i punti ottenuti in un gioco o calcolare il prezzo totale di alcuni oggetti.
Decine e centinaia non ti spaventano? Adesso il limite sale a 1000! Progredendo, impariamo a fare addizioni fino a 1000, che ci permettono di lavorare con numeri più grandi e di affrontare problemi più complessi. Ad esempio, 450 + 320 ci dà 770. Queste addizioni sono importanti per situazioni come calcolare il totale di più articoli costosi, sommare lunghe liste di numeri o gestire grandi quantità di dati.
In questo modo possiamo andare avanti a contare aggiungendo sempre più cifre.
Mappa mentale sull’addizione
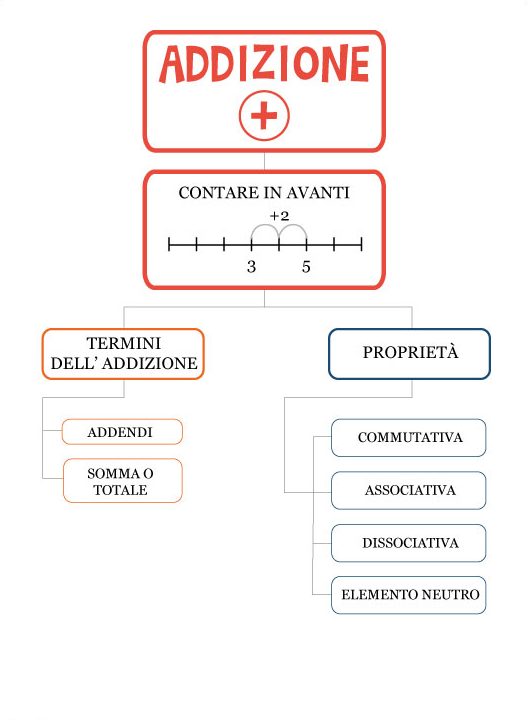
Mappa dell’addizione da scaricare:
Schede di esercizi con le addizioni
La sfida continua, gli esercizi si moltiplicano!
A seguire, delle schede in livelli di difficoltà crescenti per esercitarti con le addizioni: fino al 9, fino al 20, fino al 50 e in colonna. Anche se i numeri si fanno più grandi, non ti scoraggiare!
- Addizioni fino al 9
Scarica la scheda qui:
- Addizioni fino al 20
Scarica la scheda qui:
- Addizioni fino al 50
Scarica la scheda qui:
- Addizioni in colonna
Scarica le due schede qui:
Schede di esercizi sulle proprietà
Infine, ecco un’altra scheda con gli esercizi, completa di soluzioni, per preparare la verifica sulle proprietà delle addizioni: commutativa e associativa.
Scaricala qui: