Le proprietà delle quattro operazioni: quali sono
Le quattro operazioni fondamentali della matematica – addizione, sottrazione, moltiplicazione e divisione – si costituiscono di una serie di proprietà e regole che formano la base logica e strutturale della matematica. Ad un primo sguardo, potrebbero sembrare complesse da seguire ma, con un po’ di esercizio, sarà molto più semplice di quanto può sembrare!
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Tabella delle proprietà delle operazioni
- La proprietà commutativa di addizione e moltiplicazione
- La proprietà associativa di addizione e moltiplicazione
- La proprietà distributiva della moltiplicazione
- La proprietà invariantiva della sottrazione
- La proprietà invariantiva della divisione
- L'elemento neutro dell'addizione
- L'elemento neutro della moltiplicazione
- Ordine delle operazioni nelle espressioni
- Ordine delle operazioni nelle espressioni con parentesi
Tabella delle proprietà delle operazioni
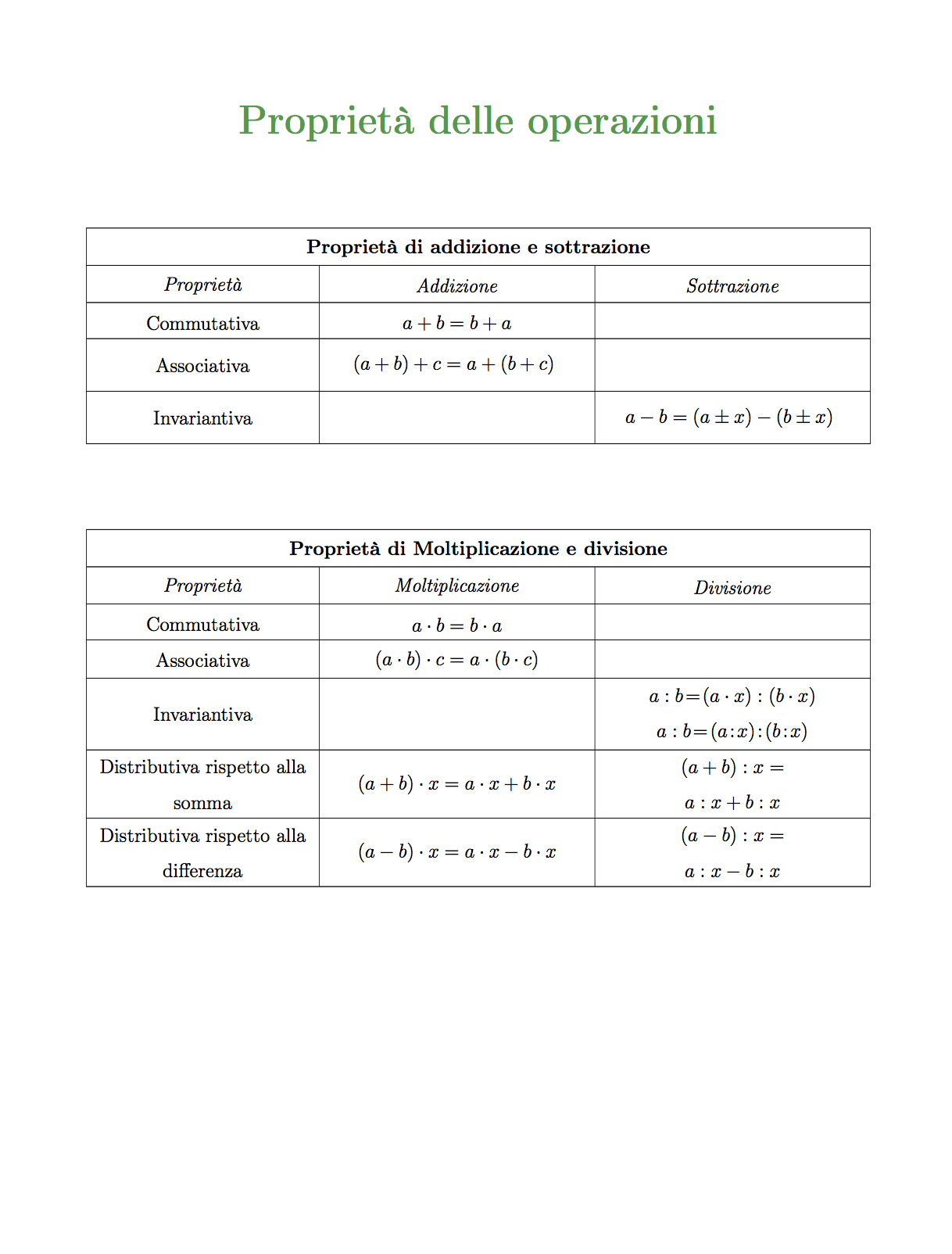
Scarica e stampa la tabella riassuntiva con tutte le proprietà delle quattro operazioni: .
Se vuoi il Formulario completo vai qui: I Formulari – Matematica – Tutte le formule dei tre anni di Scuola Media
La proprietà commutativa di addizione e moltiplicazione
Per l’addizione e la moltiplicazione vale la proprietà commutativa: scambiando l’ordine di due termini dell’operazione, il risultato non cambia.
Scambiando l’ordine degli addendi, otteniamo ancora la stessa somma.
£$ 23 + 17 = 40$£
£$ 17 + 23 = 40 $£
In qualsiasi ordine sommiamo i due termini, otteniamo lo stesso risultato.
Scambiando l’ordine dei fattori, otteniamo ancora lo stesso prodotto.
£$ 16 \cdot 3 = 48 $£
£$ 3 \cdot 16 = 48 $£
In qualsiasi ordine moltiplichiamo i due termini, otteniamo lo stesso risultato.
La proprietà associativa di addizione e moltiplicazione
L’addizione e la moltiplicazione hanno un’altra cosa in comune: la proprietà associativa.
Se sostituiamo a due numeri la loro somma, il risultato non cambia.
£$ (15 + 5) + 7 = 20 + 7 = 27 $£
ma otteniamo lo stesso risultato anche sommando per primi gli ultimi due termini
£$ 15 + (5 + 7) = 15 + 12 = 27 $£
Se sostituiamo a due numeri il loro prodotto, il risultato non cambia.
£$ (2 \cdot 10) \cdot 5 = 20 \cdot 5 = 100 $£
ma otteniamo lo stesso risultato anche moltiplicando per primi gli ultimi due termini
£$ 2 \cdot (10 \cdot 5) = 2 \cdot 50 = 100 $£
La proprietà associativa ci permette di scegliere quali somme o quali prodotti fare per primi: in una catena di somme o di prodotti, non importa l’ordine con cui decidiamo di associare i diversi fattori.
La proprietà distributiva della moltiplicazione
La moltiplicazione ha un’ulteriore proprietà che le permette di combinarsi con l’addizione. La proprietà distributiva della moltiplicazione rispetto alla somma, infatti, ci permette di distribuire le operazioni rendendo i calcoli più semplici.
Moltiplicare un numero per una somma equivale a moltiplicare quel numero per ciascuno dei termini dell’addizione, quindi sommare tutti i risultati delle moltiplicazioni.
£$ 6 \cdot (7 + 9) = 6 \cdot 16 = 96 $£
È una moltiplicazione difficile, che non siamo abituati a fare. Proviamo a distribuire la moltiplicazione sull’addizione, moltiplicando il fattore per ciascun termine tra parentesi:
£$ 6 \cdot ( 7 + 9) = 6 \cdot 7 + 6 \cdot 9 = 42 + 54 = 96 $£
Otteniamo lo stesso risultato, facendo un passaggio in più, ma con conti decisamente più semplici. È una proprietà utile quando non abbiamo a disposizione una calcolatrice per fare i conti, ma possiamo contare solo sulle nostre forze!

La proprietà distributiva della moltiplicazione rispetto alla differenza ci permette di “distribuire" le operazioni rendendo i calcoli più semplici.
Quando dobbiamo moltiplicare un numero per una differenza, invece di svolgere subito la differenza, possiamo fare due moltiplicazioni (più facili) e sottrarre solo alla fine.
La proprietà invariantiva della sottrazione
La sottrazione è l’operazione inversa dell’addizione. Ha un’unica proprietà: la proprietà invariantiva.
Se aggiungiamo o togliamo una stessa quantità ad entrambi i termini della sottrazione, otteniamo lo stesso risultato.
£$ 63 – 23 = 40 $£
ma possiamo trovare lo stesso risultato applicando la proprietà e rendendo il calcolo più semplice
£$ (63 – 3) – (23 – 3) = 60 – 20 = 40 $£
Analogamente possiamo aggiungere ad entrambi i termini la stessa quantità:
£$ 87 – 52 = 35 $£
troviamo lo stesso risultato aggiungendo 3 ad entrambi i termini
£$ (87 + 3) – (52 + 3) = 90 – 55 = 35 $£
Grazie alla proprietà invariantiva, possiamo “modificare" le sottrazioni aiutandoci con operazioni più semplici che rendono il risultato finale più facilmente raggiungibile.
La proprietà invariantiva della divisione
La divisione è l’operazione inversa della moltiplicazione. Ha solo la proprietà invariantiva.
Se moltiplichiamo o dividiamo i due termini della divisione per uno stesso numero, il risultato non cambia.
£$ 48 : 16 = 3 $£
ma se dividiamo entrambi i membri per 2, otteniamo un’operazione più semplice da risolvere
£$ (48 : 2) : (16 : 2) = 24 : 8 = 3 $£
La stessa proprietà vale se moltiplichiamo entrambi i termini per uno stesso numero:
£$ 12 : 6 = 2 $£
moltiplicando entrambi i termini per uno stesso numero, otteniamo lo stesso risultato
£$ (12 \cdot 3) : (6 \cdot 3) = 36 : 18 = 2 $£
La proprietà invariantiva della divisione può essere utile per semplificare i conti, riconducendoci ad operazioni che sono più semplici, anche solo per un fatto di abitudine.
L’elemento neutro dell’addizione
Esiste un numero che si comporta in un modo un po’ strano quando risolviamo un’addizione.
Se sommiamo lo 0 ad un numero qualsiasi, otteniamo come risultato il numero stesso. Lo 0 è l’elemento neutro dell’addizione.
£$ 13 + 0 = 0 + 13 = 13 $£
£$ 3489 + 0 = 0 + 3489 = 3489 $£
Nella sottrazione, invece, lo 0 non ha la stessa proprietà che ha per l’addizione:
£$ 56 – 0 = 56 $£, ma cosa succede invece se calcoliamo £$ 0 – 56 = ? $£
Per questo la sottrazione non ha un elemento neutro.
L’elemento neutro della moltiplicazione
Esiste anche un numero che si comporta in un modo un po’ strano quando risolviamo una moltiplicazione.
Se moltiplichiamo per 1 un numero qualsiasi, otteniamo come risultato il numero stesso. L’1 è l’elemento neutro della moltiplicazione.
£$ 7 \cdot 1 = 1 \cdot 7 = 7 $£
£$ 251 \cdot 1 = 1 \cdot 251 $£
Nella divisione, invece, l’1 non ha la stessa proprietà che abbiamo visto per la moltiplicazione:
£$ 89 : 1 = 89 $£, ma cosa succede invece se calcoliamo £$ 1 : 89 = ? $£
Per questo la divisione non ha un elemento neutro.
Ordine delle operazioni nelle espressioni
Per risolvere un’espressione, dobbiamo seguire delle regole: ogni operazione va risolta seguendo un ordine ben preciso.
Nel caso di espressioni senza parentesi, possiamo ricordare l’ordine delle operazioni con questo motto: prima i puntini, poi i trattini. Quando scriviamo puntini intendiamo la moltiplicazione e la divisione (infatti le scriviamo con dei puntini £$ \cdot $£ e £$ : $£), mentre con i trattini intendiamo l’addizione e la sottrazione (infatti le scriviamo con dei trattini £$ + $£ e £$ – $£).
£$ 3 \cdot 2 + 8 : 4 – 5 = ? $£
Calcoliamo prima moltiplicazioni e divisioni:
£$ 3 \cdot 2 + 8 : 4 – 5 = 6 + 2 – 5 = $£
Poi addizioni e sottrazioni:
£$ 6 + 2 – 5 = 3 $£
Ecco il risultato della nostra espressione!
Per risolvere correttamente un’espressione, quindi, dobbiamo prima occuparci di moltiplicazioni e divisioni, poi di addizioni e sottrazioni.
Ordine delle operazioni nelle espressioni con parentesi
Nel caso in cui compaiano anche le parentesi in un’espressione, dobbiamo ricordarci di rispettare quanto appena stabilito (prima i puntini, poi i trattini), aggiungendo però la regola delle parentesi.
Dovremo risolvere prima le operazioni all’interno delle parentesi tonde, poi quelle all’interno delle parentesi quadre e solo per ultime le operazioni all’interno delle parentesi graffe.
£$ \{35 – [5 \cdot 2 + 16 : (2 \cdot 8 : 4)] \} + 1 = ? $£
Iniziamo a risolvere le operazioni all’interno della parentesi tonda, ricordandoci la regola: prima i puntini, poi i trattini.
£$ \{35 – [5 \cdot 2 + 16 : (2 \cdot 8 : 4)] \} + 1 = \{ 35 – [5 \cdot 2 + 16 : (16 : 4)] \} + 1 = \{ 35 – [5 \cdot 2 + 16 : 4] \} + 1 = $£
Quindi risolviamo le operazioni all’interno della parentesi quadra:
£$ \{ 35 – [5 \cdot 2 + 16 : 4] \} + 1 = \{ 35 – [10 + 4] \} + 1 = \{ 35 – 14 \} + 1 = $£
Ora possiamo risolvere anche le operazioni nella parentesi graffa:
£$ \{ 35 – 14 \} + 1 = 11 + 1 $£
E quindi concludere la nostra espressione trovando il risultato finale:
£$ 21 + 1 = 22 $£
In caso di espressioni con le parentesi, ricorda di risolvere in ordine le operazioni nelle: parentesi tonde, parentesi quadre e infine parentesi graffe.
