Le addizioni e le sottrazioni con i numeri relativi

I numeri relativi, noti anche come numeri interi, includono l’intero insieme dei numeri positivi, negativi e lo zero, estendendo così il campo numerico al di là dei familiari numeri naturali. Le operazioni di addizione e sottrazione con questi numeri possono sembrare inizialmente intimidatorie, ma seguendo regole semplici e logiche diventano accessibili a tutti.

L’addizione e la sottrazione di numeri relativi sono governate da principi che determinano come i segni, positivi e negativi, interagiscano tra loro. Quando si sommano due numeri con lo stesso segno, il risultato mantiene quel segno e si sommano i valori assoluti dei numeri. Al contrario, quando si sommano due numeri con segni opposti, si sottraggono i loro valori assoluti, e il segno del risultato corrisponde al segno del numero con il valore assoluto maggiore. Per la sottrazione, si segue la regola di aggiungere l’opposto del sottraendo, trasformando così ogni sottrazione in una addizione.

Scopriamo insieme come fare!

• Come calcolare le addizioni con i numeri relativi
• Sottrazioni con i numeri relativi: come calcolarle
• Somma algebrica con i numeri interi
• Somma algebrica con i numeri razionali
• Le proprietà della somma algebrica con i numeri relativi

Come calcolare le addizioni con i numeri relativi

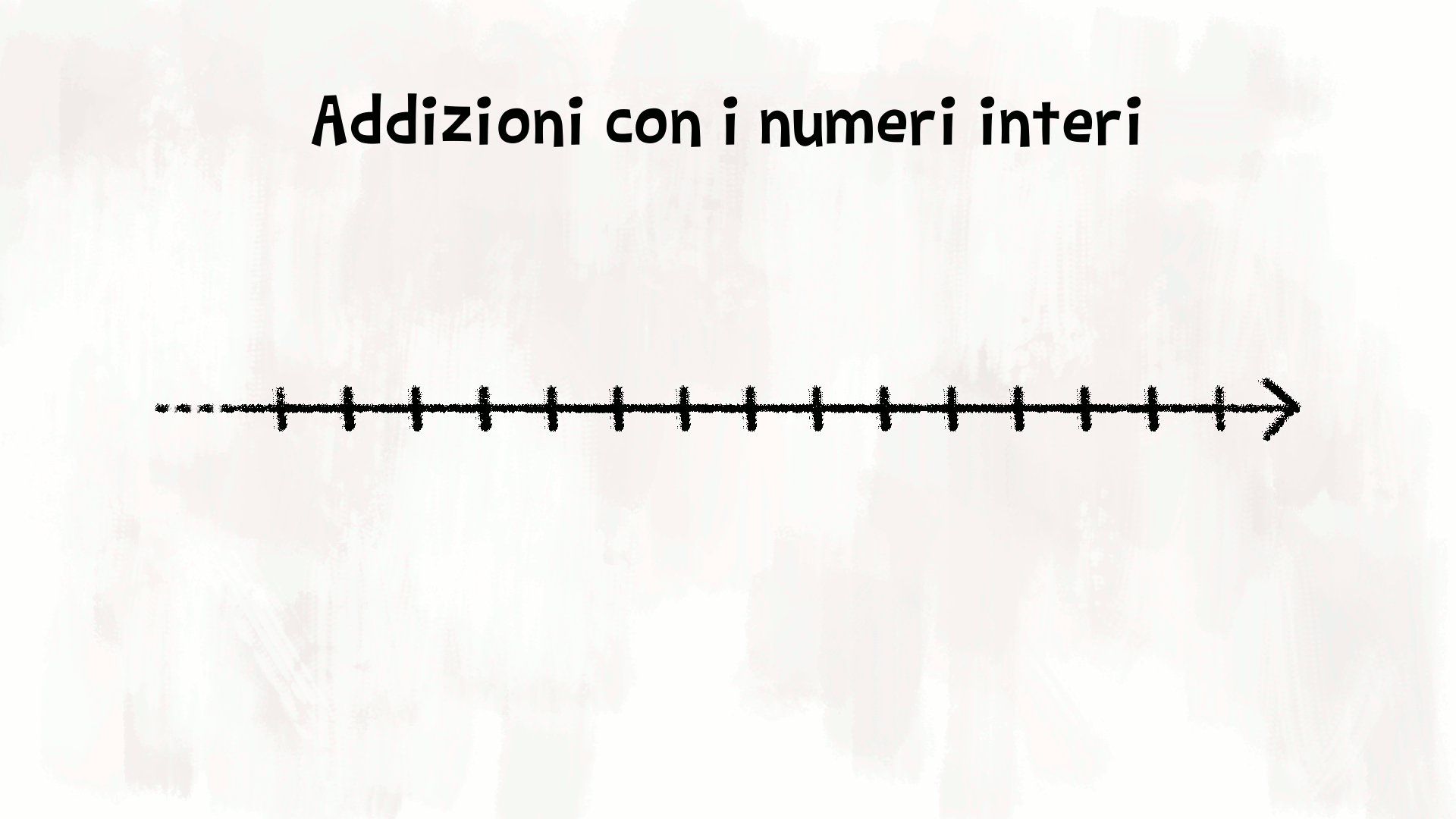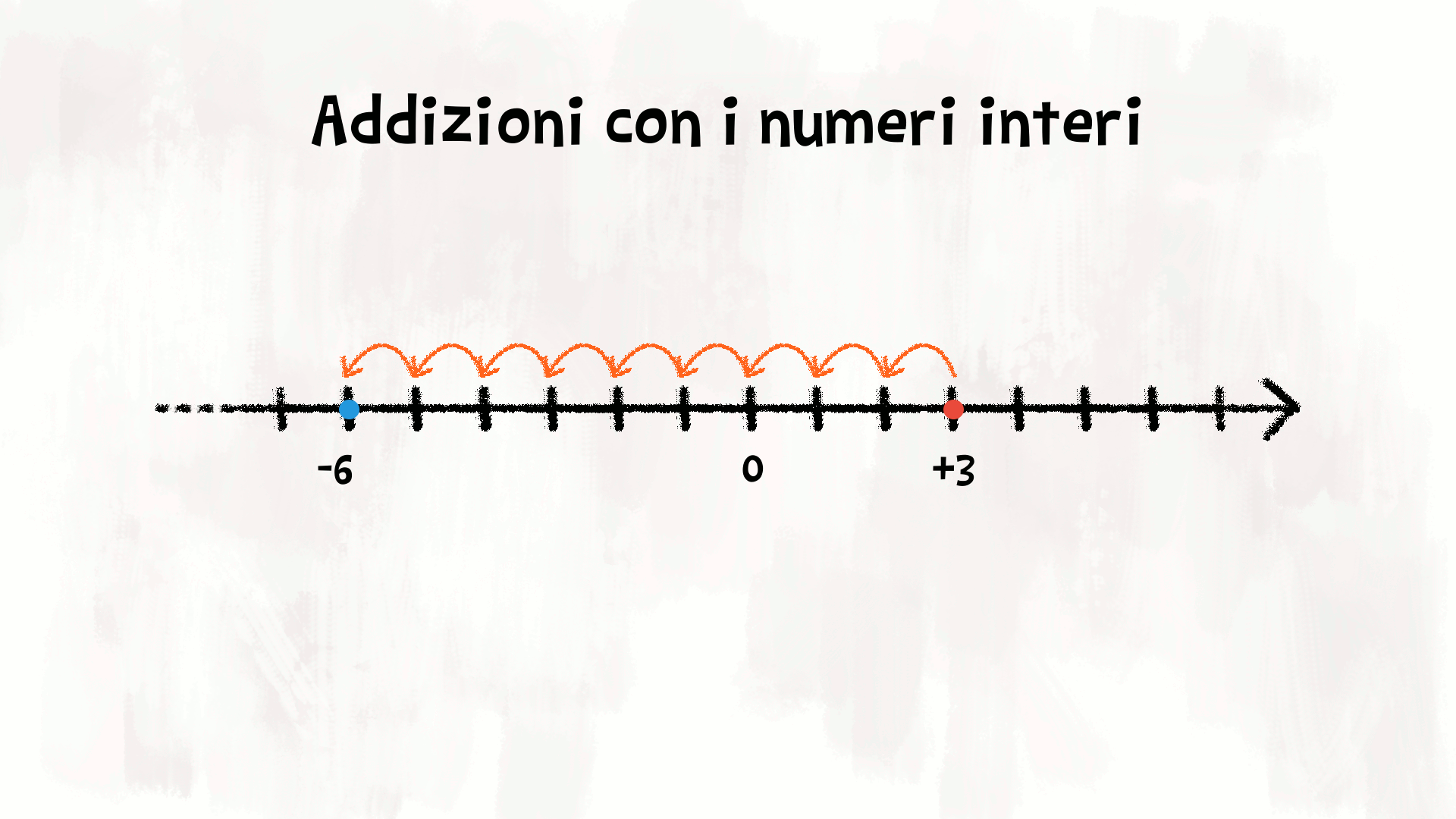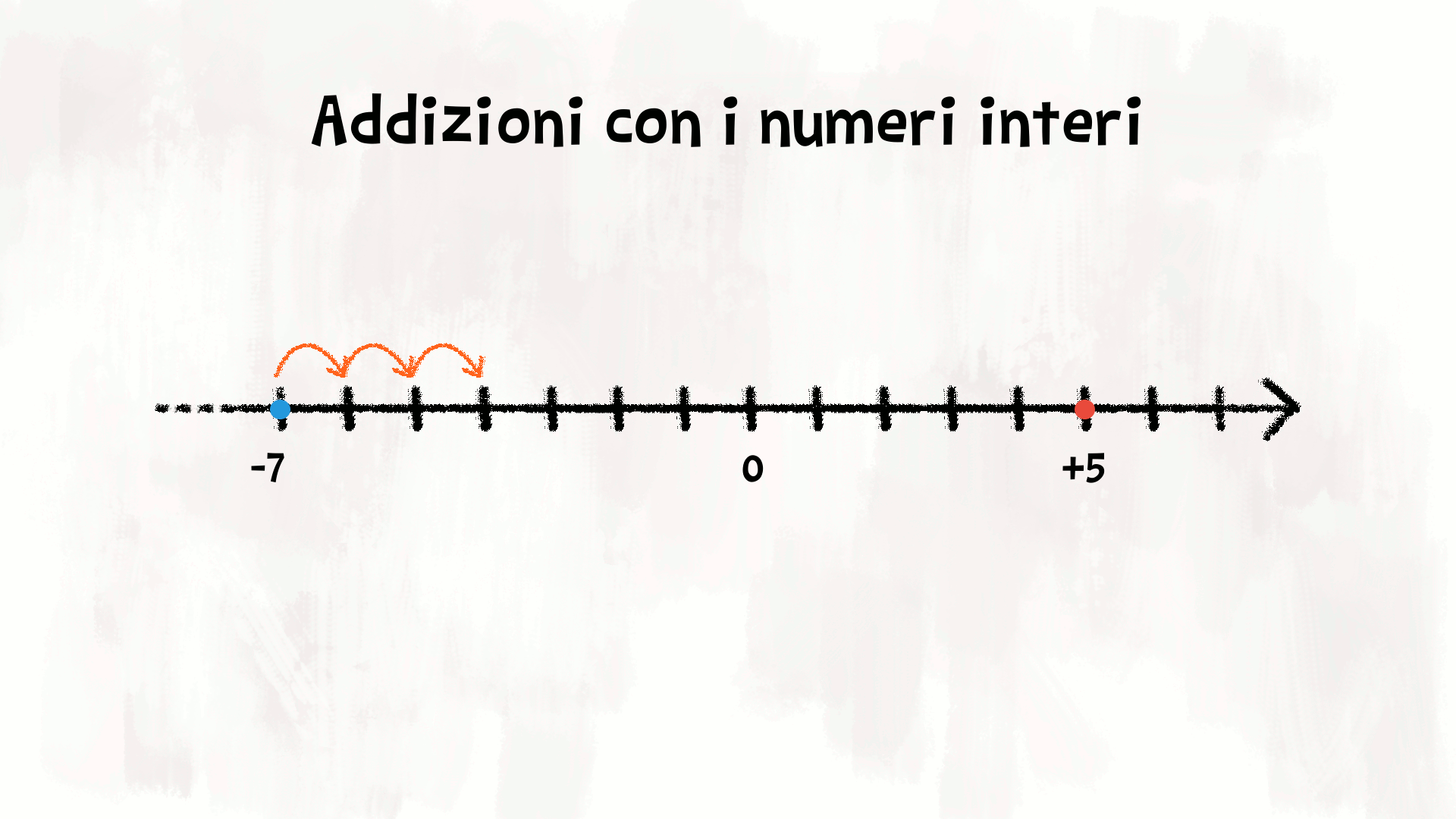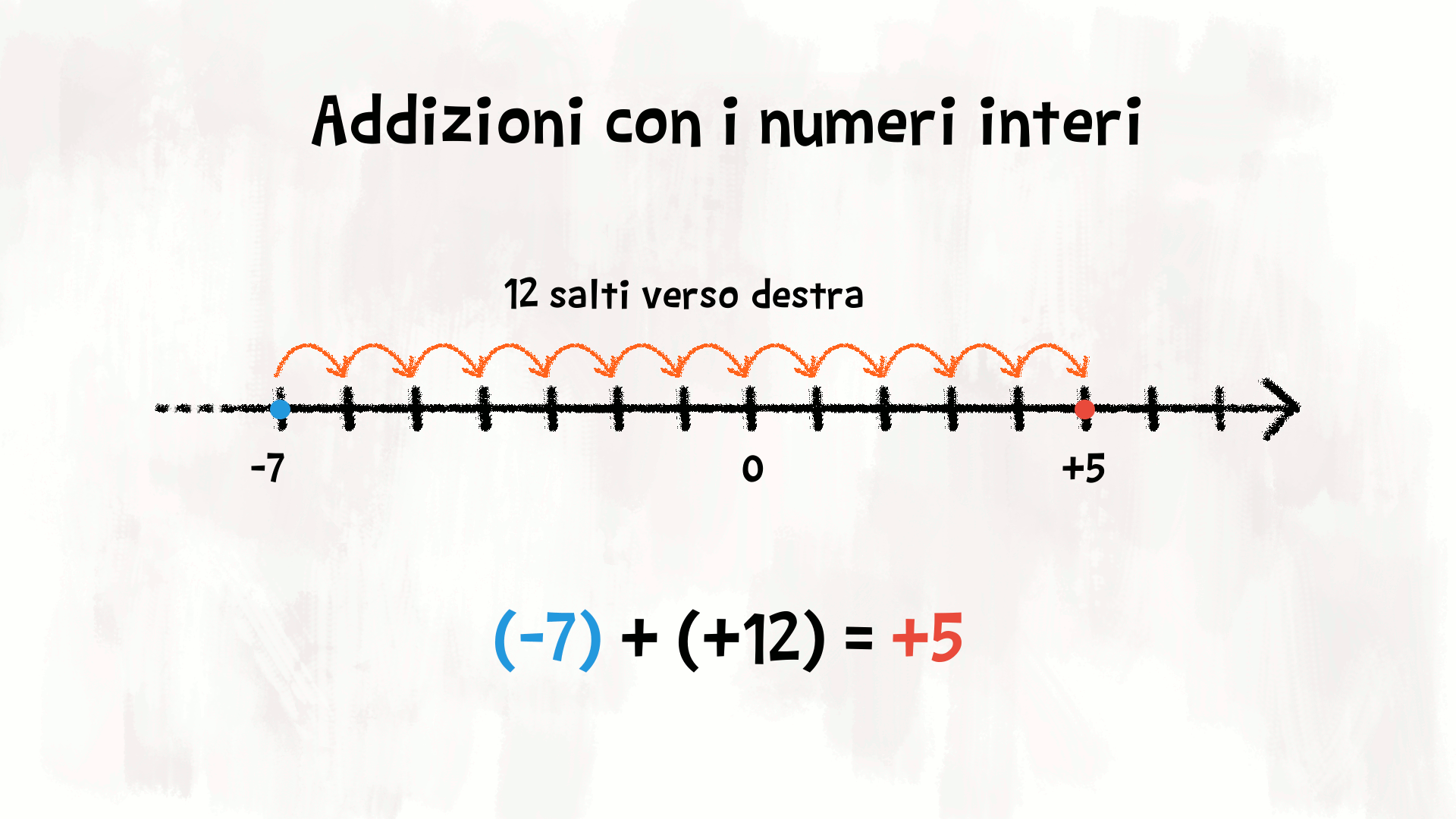
Abbiamo già trovato il risultato di qualche semplice addizione, percorrendo verso destra o verso sinistra la retta dei numeri.

Sommiamo due numeri interi!

Se gli addendi hanno lo stesso segno, sommiamo i loro valori assoluti e poi aggiungiamo il segno degli addendi.

Esempi:

• £$ (+5) + (+6) $£, gli addendi hanno lo stesso segno positivo.
  Sommiamo come al solito £$ 5 + 6 = 11 $£ e poi aggiungiamo il segno £$ + $£.Il risultato è £$ (+5) + (+6) = +11 $£.
• £$ (-4) + (-3) $£, gli addendi hanno lo stesso segno negativo.
  Sommiamo come al solito £$ 4 + 3 = 7 $£ e poi aggiungiamo il segno £$ – $£.
  Il risultato è £$ (-4) + (-3) = -7 $£.

Se gli addendi hanno segno opposto, guardiamo ai loro valori assoluti: il risultato avrà il segno del termine con valore assoluto maggiore!

Esempi:

• £$ (-5) + (+6) $£ è una somma di numeri discordi. Il primo ha valore assoluto £$ 5 $£, il secondo ha valore assoluto £$ 6 $£. Poiché [iol_placeholder type="formula" engine="katex" display="inline"] 5 Il risultato è £$ (-5) + (+6) = +1 $£.
• £$ (+3) + (-4) $£ è una somma di numeri discordi. Il primo ha valore assoluto £$ 3 $£, il secondo ha valore assoluto £$ 4 $£. Poiché [iol_placeholder type="formula" engine="katex" display="inline"] 3 Il risultato è £$ (+3) + (-4) = -1 $£.

Ricorda! La somma di due numeri opposti è sempre £$ 0 $£!
£$ (+7) + (-7) = 0 $£
£$ (-2) + (+2) = 0 $£

Sottrazioni con i numeri relativi: come calcolarle

E se vogliamo sottrarre due numeri interi?
In realtà sappiamo già farlo… basta trasformare ogni sottrazione in una addizione.

Sottrarre da un numero intero un altro numero intero equivale a sommare il primo all’opposto del secondo.

Esempi:
£$ (+5) – (+2) = (+5) + (-2) = +3 $£
£$ (-5) – (-2) = (-5) + (+2) = -3 $£
£$ (+5) – (-2) = (+5) + (+2) = +7 $£
£$ (-5) – (+2) = (-5) + (-2) = -7 $£

Somma algebrica con i numeri interi

Abbiamo visto che dietro ogni sottrazione si nasconde una addizione. È per questo che l’addizione e la sottrazione con i numeri interi si possono fondere in un’unica operazione chiamata somma algebrica.

Tutte le seguenti operazioni sono somme algebriche:

£$ (+5) + (+2) $£
£$ (-5) – (-2) $£
£$ (+5) + (-2)$£
£$ (-5) – (+2) $£

Per sommare due numeri relativi, possiamo liberarci di tutte le parentesi rispettando le regole dei segni:

• il segno £$ + $£ davanti alla parentesi ci permette di lasciare i segni invariati;
• il segno £$ – $£ davanti alle parentesi fa cambiare segno ai numeri al loro interno.

Esempi:
£$ (+5) + (+2) = +5 +2=+7$£
£$ (-5) + (+2) =-5 + 2=-3$£
£$ (+5) + (-2) = +5 – 2=+3$£
£$ (-5) + (-2) = -5 – 2=-7$£

Ogni espressione costituita da somme algebriche tra numeri interi si può riscrivere in una forma più semplice e elegante senza le parentesi.

£$ (-3) + (+5) – (-2) + (-1) – (+8) – (-4) =$£
£$ = -3 + 5 + 2 – 1 -8 + 4 = -1 $£

Somma algebrica con i numeri razionali

E questa scrittura £$ \left(-\frac32\right) $£ che cosa vuol dire?

£$ \left(-\frac32\right) $£ è
una frazione con segno negativo.

Anche i numeri razionali possono essere positivi o negativi!
£$ \left(-\frac32\right) $£ è la
frazione opposta della frazione £$ \left(+\frac32\right) $£, cioè
£$ \left(-\frac32\right) + \left(+\frac32\right) =0 $£

Per eseguire addizioni e sottrazioni con frazioni con segno positivo o negativo basta seguire le regole che abbiamo già incontrato per le operazioni con frazioni e le operazioni con numeri interi.

Fai attenzione alle differenti scritture!

£$ \left(-\frac32\right) $£ è equivalente a £$ \left(\frac{-3}2\right) $£ e anche a £$ \left(\frac3{-2}\right) $£

£$ \left(\frac53\right) $£ è equivalente a £$ \left(\frac{-5}{-3}\right) $£

Le proprietà della somma algebrica con i numeri relativi

In un’espressione con somme algebriche di numeri positivi e negativi, una volta tolte le parentesi, possiamo applicare due proprietà che già conosci molto bene: la proprietà commutativa e la proprietà associativa dell’addizione che valgono anche con i numeri negativi!

Utilizzare queste proprietà ti può aiutare molto ad eseguire i calcoli più complessi.

Ti ricordi che cosa dicono?

Proprietà commutativa dell’addizione:
£$ a + b = b + a $£

Esempio: £$ (-3) + (+6) = (+6) + (-3) = +3$£

Proprietà associativa dell’addizione:
£$ a + (b + c) = (a + b) + c $£

Esempio: £$ (-3) + ((-2) + (+6)) = ((-3) + (-2)) + (+6) = +1 $£